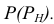Вспомогательная плоскость способ вспомогательных плоскостей

Способ вспомогательных секущих плоскостей в начертательной геометрии с примером

Способ вспомогательных секущих плоскостей:

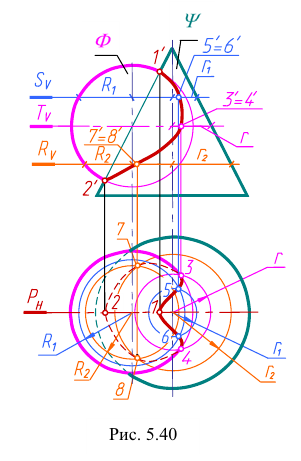
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис.5.40).

Для построения линии пересечения заданных поверхностей в ка­честве вспомогательных плоскостей необходимо использовать фронтальную плоскость Р и ряд горизонтальных плоскостей (S, Т, R).

Построение начинаем с определения проекций характерных точек. Проводим фронтальную плоскость

Вспомогательные горизонтальные плоскости пересекают сферу и конус по окружностям.

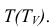
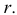
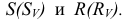
Проекции 3′ и 4′ точек, лежащих на экваторе сферы, находим с помощью горизонтальной плоскости Она проходит через центр сферы. Плоскость пересекает сферу по экватору и конус по окружности радиуса В пересечении горизонтальных проекций этих линий и нахо­дим горизонтальные проекции 3 и 4 . Горизонтальные проекции точек 3 и 4 являются точками границы видимости линии пересечения на этой проекции. Промежуточные точки (точки 5, 6, 7, X) находим с помощью вспомогательных горизонтальных плоскостей Полученные точки соединим плавной кривой линией с учетом видимости.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Способ вспомогательных сфер
• Выполнение и оформление чертежей по ГОСТ и ЕСКД
• Виды в инженерной графике
• Разрезы в инженерной графике
• Построение проекций линий пересечения конуса плоскостью
• Развертка поверхности конуса
• Шаровая поверхность
• Винтовые поверхности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Метод вспомогательных секущих плоскостей

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересечении с данными поверхностями образуют простые для построения линии (прямую или окружность).

13.2.1. Задание:даны поверхности конуса 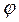и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.

Решение:ось цилиндра перпендикулярна к плоскости П₂,следовательно, поверхность цилиндра — проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные — наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции 1₁и 2₁ принадлежат горизонтальной проекции очерковой образующей конуса (l₁ и 2₁, совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.

Для определения их горизонтальных проекций через ось цилиндра параллельно П₁проводят вспомогательную секущую плоскость Г (ее фронтальный след Г₂).

Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиуса R, которая на П₁будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек 3₁и 4₁ (рис. 13.3).

Построение промежуточных точек аналогично построению точек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).

13.3.1. Задание:Даны две поверхности вращения — конус и цилиндр, оси которых пересекаются и находятся в одной плоскости, параллельной П₂(рис. 13.5). Требуется построить линию их пересечения.

Решение:на фронтальной проекции фиксируют точки пересечения заданных поверхностей вращения 1₂ и 2₂ — они при­надлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра – 1₁ и 2₁.Другие точки линии пересечения можно построить, используя концентрические сферические поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая — касательная к проекции конуса, а последующие — большим радиусом (рис. 13.6).

Каждая сфера пересекает обе поверхности по окружностям, фронтальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.

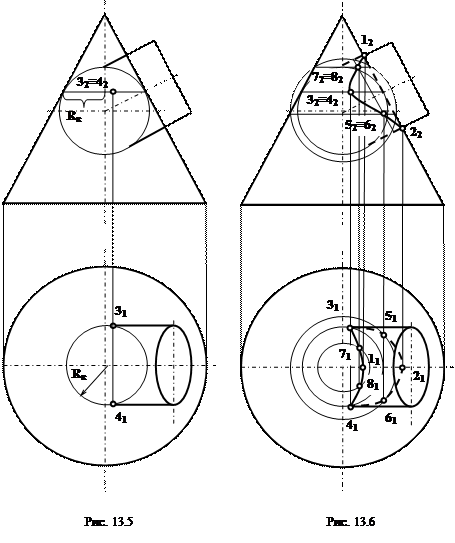
Горизонтальные проекции этих точек определяются по принадлежности одной из поверхностей. В данном случае удобнее их получать по принадлежности конусу. Например, точки 3и 4лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рис. 13.6). Чтобы определить видимость горизонтальной проекции линии пересечения, на её фронтальной проекции отмечают точки, лежащие на проекции осевой линии цилиндра и принадлежащие линии пересечения.

Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных, будут находиться на не­видимой части цилиндра.

Источник

Метод вспомогательных секущих плоскостей

Для построения линии пересечения двух поверхностей часто применяют метод вспомогательных секущих плоскостей. Смысл этого метод заключается в том, что вводят дополнительную секущую плоскость, которая пересекает обе поверхности. Затем строят линии пересечения обеих поверхностей секущей плоскостью. Точка пересечения этих линий и есть общая точка этих поверхностей. Пересекая поверхности рядом дополнительных плоскостей, получают множество точек, общих для пересекающихся поверхностей.

Как выбрать положение или вид этих вспомогательных плоскостей?

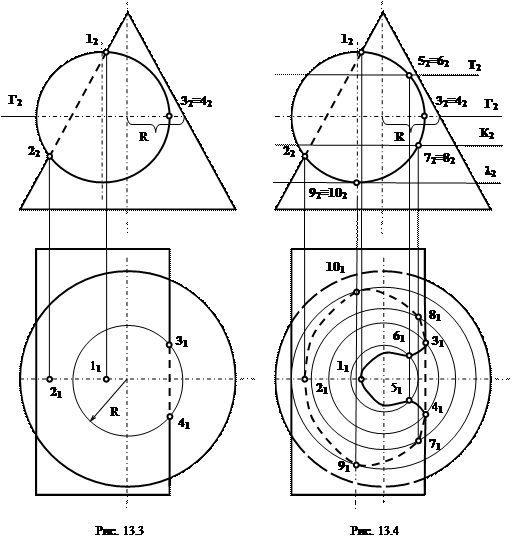
Дополнительные плоскости подбирают таким образом, чтобы они в пересечении с поверхностями давали простые линии пересечения, например, окружности или прямые. Кроме того, эти линии при проецировании на плоскости проекций, должны проецироваться в натуральную величину. Для этих целей подходят обычно плоскости уровня. Рассмотрим на примере работу с одной плоскостью, которую выберем перпендикулярно оси вращения конуса (рис.25).

При решении задач по построению линии пересечения поверхностей необходимо находить характерные точки линии пересечения. Эти точки, как правило, являются точками пересечения очерковых образующих, если поверхности имеют общую ось симметрии, как в примере, рассмотренном на рис.25. Так как эти точки лежат на очерке (точки С и К), то их горизонтальные проекции лежат на оси симметрии поверхностей (рис.26).

Источник

Способ вспомогательных проецирующих плоскостей (способ конкурирующих линий)

Способ вспомогательных проецирующих плоскостей (способ конкурирующих линий)

• Список вспомогательных проекционных плоскостей (как конкурировать) 1. Как упомянуто выше, конструкция пересечения двух поверхностей посредством вспомогательной плоскости проекции находится на плоскости проекции, которая пересекает данные обеих поверхностей по графически простой линии (прямая или окружность).

• Пересечение этих линий обеспечивает точки, которые принадлежат желаемой линии. Поскольку линии пересечения между каждой вспомогательной плоскостью проекции и этими поверхностями являются конкурирующими линиями, метод вспомогательной плоскости проекции приводит к рисованию простых графических линий, которые конкурируют друг с другом на этих поверхностях.

Вот так Если пересекающиеся поверхности имеют семейство графически простых линий, которые конкурируют друг с другом, точка пересечения этих линий представляет интерес. Людмила Фирмаль

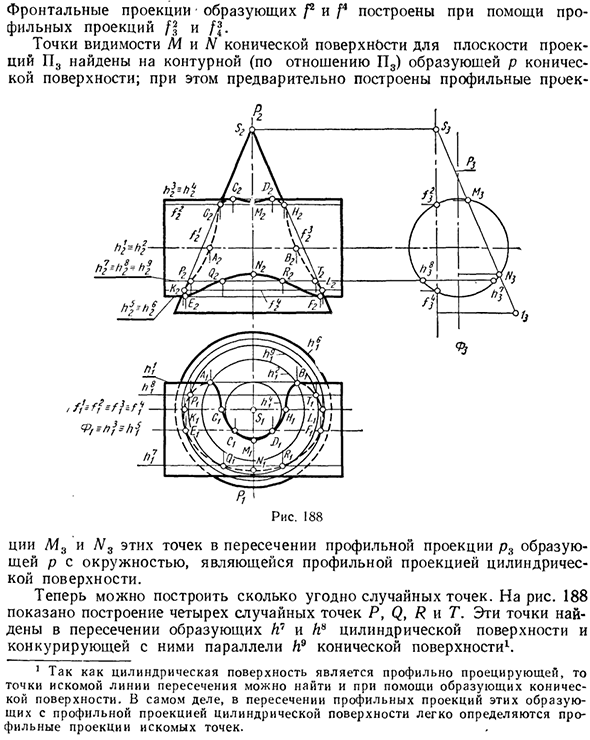
Рассмотрим пример построения пересечения двух поверхностей. Пример 1. Нарисуйте пересекающуюся линию между вращающимся конусом и вращающимся цилиндром, оси которого пересекаются под прямым углом (рис. 188). Эти линии пересечения поверхности могут быть нарисованы с использованием конкурирующих линий.

Фактически, когда вы рисуете генераторы (прямые линии) на цилиндрической поверхности, каждый из них конкурирует с конической параллелью (круг). Поскольку эти параллельные линии горизонтальны, они не будут искажаться в плоскости проекции nt. Сначала показано строительство контрольной точки.

В цилиндрической плоскости это видимые точки | точек A и B на плоскости проекции P, но они также являются самыми дальними точками. Эти точки находятся на пересечении контурной линии цилиндрической поверхности h1 и параллельной ей конической поверхности L2.

Коническая поверхность видимой точки плоскости проекции P | No, потому что видна вся поверхность этой плоскости проекции. Видимые точки C, D, E, F на цилиндрической поверхности плоскости проекции P2 были обнаружены на пересечении генераторов контуров цилиндрических поверхностей L3 и h5 и соответствующих им параллельных параллельных линий L4 и / или L4.

Кроме того, точки C и D являются самыми высокими, а точки E и F — самыми низкими. Видимые точки G, I, K, L конической поверхности плоскости P2 проекции находятся на пересечении генераторов контура f1 и P конической поверхности и, следовательно, на пересечении конкурирующих генераторов f2 и f * цилиндрической поверхности.

Фронтальная проекция генераторов f2 и f * является профильной проекцией /? Построен с использованием Видимые точки M и N конической поверхности плоскости P3 проекции лежат на контуре (относительно P3), который образует p конической поверхности. В то же время, дизайн профиля A13 и A / 3 этих точек на пересечении проекции контура p3, которая образует окружность, и p, который является проекцией контура цилиндрической поверхности.

Теперь вы можете создать столько случайных точек, сколько захотите. На рисунке 188 показана структура четырех случайных точек P, Q, R и T. Эти точки находятся на пересечении генераторов A7 и h * на цилиндрической поверхности и конической поверхности, параллельной им. 1 Поскольку цилиндрическая поверхность является профильной проекцией, Интересную точку пересечения можно также найти с помощью генератора конуса Поверхность.

• На самом деле, на пересечении этих профилей проекций Те с цилиндрической проекцией профиля поверхности легко определить Файл проекции нужной точки. После того как вы построили достаточное количество случайных точек на линии пересечения, вам необходимо соединить их в определенном порядке с учетом условий видимости.

В этом случае видимость линии пересечения обоих проекционных полей определяется цилиндрической гранью. Следовательно, отображается только участок пересекающейся линии в видимой части цилиндрической грани 1. 2. При создании пересечения двух поверхностей, если хотя бы одна проецируется, необходимо использовать уменьшение проекции этой поверхности на линию.

Кроме того, строительство наземных линий пересечения значительно упрощается. Людмила Фирмаль

Это связано с тем, что одна из проекций в этой точке принадлежит вырожденной проекции плоскости проекции, а другая проекция легко определяется с помощью простой графической линии на второй плоскости. Это показано в следующем примере. Пример 2.

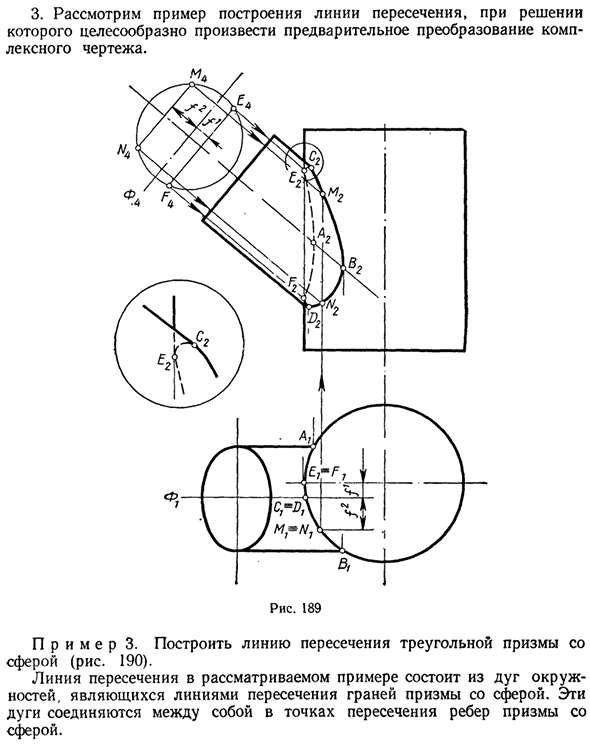
Нарисуйте пересекающуюся линию двух вращающихся цилиндров с пересекающимися осями, и один из них проецируется горизонтально (рис. 189). Поскольку поверхность одного из этих цилиндров проецируется горизонтально, горизонтальная проекция желаемой пересекающейся линии совпадает с дугой окружности AXB окружности, которая является горизонтальной проекцией этого цилиндра.

Чтобы определить фронтальную проекцию линии пересечения, постройте ее, используя графически простую линию. В этом случае передняя проекция точки должна быть определена, образуя второй цилиндр Х-линия на пересечении поверхностей. На рисунке 189 показаны контрольные точки A и B (самая дальняя, ближайшая).

C и D (самая высокая, самая низкая, вторая цилиндрическая точка видимости в плоскости проекции P2), £ и F (крайняя слева, они Показана конфигурация передней проекции плоскости) А2) видимости первого цилиндра и случайных точек А1 и N Отметим, что прямую проекцию точек E, F и случайных точек M, N удобнее всего найти, заменив плоскость проекции nt плоскостью P4, перпендикулярной образующей второго цилиндра.

Этот цилиндр затем проецируется в форме круга на плоскость P4 и может быть легко построен с использованием проекций El, F4, M4, yV4 желаемой точки с использованием глубин f1 и f. Фронтальная проекция этих точек легко определяется. В другом круге элементы, которые пересекают видимые точки C и £, отображаются в увеличенном виде.

На рисунке 188 и последующих чертежах, показывающих пересечение одной фигурной поверхности, каждый из этих поверхностных элементов не находится внутри другой поверхности. Другими словами, на этих чертежах предполагается, что каждая приемлемая поверхность отсекает часть другой поверхности, заключенную в первой поверхности. 3.

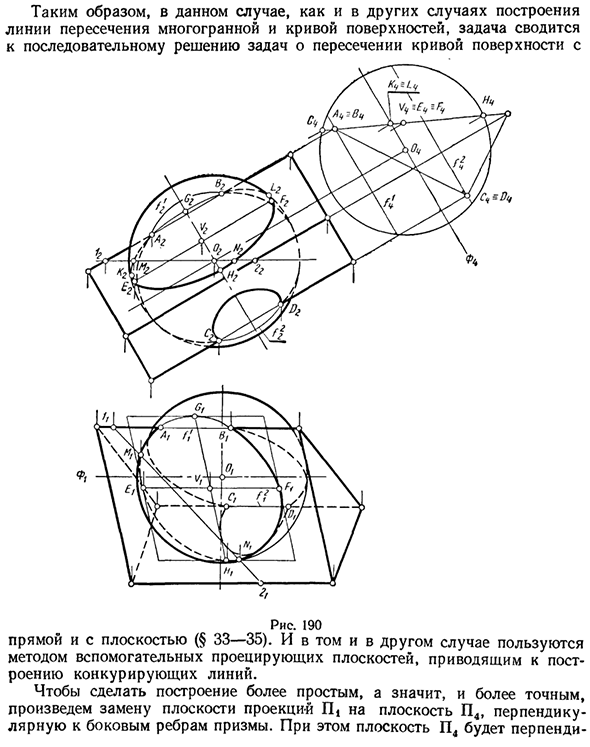
Рассмотрим пример создания линии пересечения. Рекомендуется заранее конвертировать сложные чертежи. Пример 3. Нарисуйте линию пересечения между треугольной призмой и сферой (рисунок 190). Линия пересечения в этом примере состоит из дуг. Это пересечение лица призмы и сферы. Эти дуги взаимосвязаны на пересечении края призмы и сферы.

Следовательно, в этом случае задача сводится к последовательному решению проблемы пересечения криволинейной поверхности с криволинейной поверхностью, как и в других случаях построения линии пересечения между многогранником и криволинейной поверхностью. Рисунок 190 Прямые линии и плоскости (§33–35). В обоих случаях используется метод вспомогательной проекционной плоскости, что приводит к построению конкурирующих линий.

Чтобы упростить конструкцию и, следовательно, сделать ее более точной, мы заменяем плоскость проекции P плоскостью P4, перпендикулярной боковому краю призмы. В этом случае плоскость P4 перпендикулярна В системе (II |, II) эти ребра являются передними, поэтому они являются круглыми относительно плоскости A2.

Далее в системе (P2, P4) стороны призмы выступают относительно плоскости P4. Это значительно облегчает построение желаемой линии пересечения. Используйте передние f1 и f2 этой сферы, которые конкурируют с соответствующим боковым краем призмы, чтобы найти точки A, B и C, D на пересечении края призмы и сферы (§35, Пример 2).

Затем нарисуйте линии пересечения со сферой и каждой из трех сторон призмы (§34, пример 3). На чертеже (рисунок 190) подробно показан состав линии пересечения между сферой и только одной стороной призмы, то есть плоскость, которая появляется на обеих основных гранях проекции. Сначала найдите центр V круга. Это желаемая линия пересечения. Для этого опустите перпендикуляр от точки 04 к прямой (? 4 // 4.

Начало этого перпендикуляра определяет проекция V4 центра V. Затем основные проекции V2 и V, центр V Передняя проекция отрезка G4tf4 линии пересечения определяется его осями E2F2 и G2H2, но ось E2FZ равна диаметру ok-ie и равна отрезку G4 # 4, а проекция P2 Найти точку на визуальной плоскости.

Рисунок 19! Пушка, мост К и Л Чтобы создать эллипс, представляющий собой горизонтальную проекцию нужного круга, необходимо создать горизонтальную проекцию диаметров EF и GH, перпендикулярную друг другу желаемого круга. Эти проекции диаметра EtFt и GiHi являются сопряженным диаметром эллипса. Это позволяет вам создать сам эллипс.

В дополнение к этому должна быть определена видимая точка M n N плоскости проекции nt. Они принадлежат рассматриваемому лицу и построены с помощью прямой линии 1-2, которая конкурирует с экватором сферы. 4. Рассмотрим технический пример создания переходных линий для вращающихся цилиндров с пересекающимися осями (Рисунок 191). Используйте дополнительные плоскости проекции P3 и P4, чтобы создать несколько точек на линии перехода. Для этих проекционных плоскостей проецируются боковые цилиндры.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник