Все верные способы вычисления функции

Вычисление функций

Материал из MachineLearning.

Содержание

Введение

Приближенное вычисление функций является важной практической задачей. Для большинства случаев практических вычислений бывает достаточно уже реализованных в программных системах функций, которые, кстати, также вычисляются приближенно. Однако, если необходимо вычислять эти функции с точностью, отличной от предлагаемой, или реализовать нестандартную функцию, то непременно возникает задача приближенного вычисления. Ниже описаны несколько подходов к решению данной задачи.

Изложение метода. Анализ метода. Анализ ошибок

Интерполяция степенным рядом

Известно, что любую аналитическую функцию f(x) можно разложить в степенной ряд в окрестности некоторой точки x₀.

По известному разложению легко вычислить значение полинома, составленного из первых k членов степенного ряда в заданной точке. В общем случае вопрос о выборе числа k для достижения необходимой точности вычислений совсем не прост. Стандартная практика завершать вычисление суммы, когда модуль последнего добавленного слагаемого в определенное число раз меньше модуля накопленной суммы. К счастью, часто используемые в вычислениях элементарные функции разложимы в ряд Тейлора, хотя, как будет показано ниже, и для таких функций метод интерполяции ограниченным степенным рядом не дает желаемых результатов.

Для разложения функции f(x) в ряд Тейлора в окрестности точки x₀

cправедлива следующая оценка остаточного члена:

откуда можно найти число членов ряда, доставляющее необходимую точность приближения значения функции в точке х.

К недостаткам данного метода можно отнести наличие радиуса сходимости степенного ряда для разложения в окрестности точки x₀. Обычно радиус сходимости степенного ряда известен заранее, и с этой проблемой справляются путем замены переменной, внося ошибки округления. Но, гораздо более коварная ситуация возникает со всюду сходящимися рядами, так как зачастую они сходятся настолько медленно, что становятся непригодными для вычислений. Кроме того, абсолютная ошибка вычислений по указанной формуле распределена неравномерно и нарастает по мере удаления от точки x₀.

Полиномы Чебышева

Полиномы Чебышева первого рода представляют собой ортогональную систему функций и определяются следующим образом:

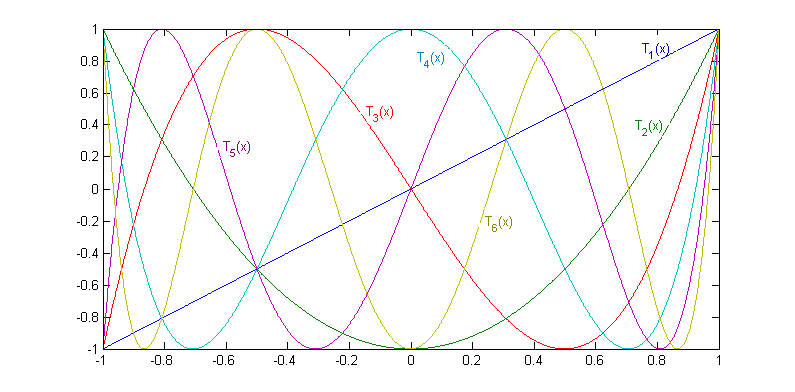
Используя тригономитрические соотношения для косинусов суммы и разности, можно вывести рекуррентное соотношение для нахождения полиномов Чебышева:

Полином T_n(x) имеет на отрезке [-1,1] ровно n корней, расположенных в точках

Любую функцию f(x), определённую на отрезке [-1,1] можно приблизить следующей формулой:

которая в точности верна для всех x,являющихся корнями многочлена T_N(x).

Преимущество разложения функции по полиномам Чебышева состоит в том, что при этом абсолютная ошибка вычислений знакопеременна и распределена более или менее равномерно по всему интервалу [-1,1]. Наилучшее приближение функции степенным рядом в том смысле, что максимальная ошибка при этом приближении минимальна, называется чебышевским приближением. Это приближение не совпадает с разложением по Чебышевским многочленам, но обычно его поиски, которые требуют больших вычислительных затрат, не оправдывают уменьшение ошибки. Т.е. приближение Чебышевскими многочленами практически совпадает с чебышевским приближением и гораздо более привлекательно в вычислительном плане.

Экономизация рядов

Метод экономизации рядов заключается в корректировке коэффициентов частичной суммы степенного ряда функции f(x). Он состоит из следующей последовательности действий:

1. Вычислить необходимое число коэффициентов степенного ряда для приближения функции f(x) с требуемой точностью на отрезке [a,b];
2. Сделать замену переменных для отображения интервала [a,b] в интервал [-1,1];
3. Найти коэффициенты разложения полученного полинома по полиномам Чебышева;
4. В полученном разложении взять первые k членов так, чтобы коэффициент при T_k+1 по абсолютной величине был меньше необходимой точности вычислений;
5. Представить полученную сумму многочленом стандартного вида;
6. Сделать обратную замену переменных.

Метод экономизации рядов позволяет распространить ошибку ограничения по всему интервалу, при этом уменьшив количество необходимых для вычисления слагаемых.

Вычисление рядов

Независимо от того, каким способом было получено разложение функции в степенной ряд — по формуле Тейлора, Чебышева или методом экономизации, — всегда бывает необходимо вычислить значение полинома вида

Метод вычисления полинома оказывает большое влияние на распространение ошибок вычисления (ошибки исходной информации и ошибки округления).

Число умножений при вычислении по данной формуле составляет . Этот полином можно переписать в несколько ином виде, после чего его можно вычислить не только быстрее, но и во многих случаях с большей точностью.

Правило Горнера

Правило Горнера, широко известный метод вычисления значений полинома, записывается в виде:

Вычисления по данной формуле производятся в соответствии с заданным порядком действий. Для вычисления полинома по правилу Горнера требуется n сложений и n умножений. Во многих практических расчетах применение правила Горнера не только экономит машинное время, но и повышает машинное время за счет уменьшения верхнего предела ошибки округления.

Параллельное вычисление многочлена

Полином степени n может быть вычислен за параллельных шагов. Процесс вычисления состоит в следующем:

1. На вход алгоритму подается вектор коэффициентов исходного многочлена, при необходимости дополненный нулем, для того, чтобы вектор имел четную длину; k=0.
2. Соседние элементы вектора попарно суммируются, причем второй член суммы умножается на x 2 k , где k — это номер итерации. Таким образом, на выходе мы получим вектор в два раза меньшей длины. Полученный вектор также дополняется нулем, в случае необходимости; k=k+1.
3. Шаг 2 повторяется до тех пор, пока длина вектора на выходе не станет единичной.

Данный метод, в общем случае, имеет меньшую ошибку округления, чем метод последовательного вычисления.

Суммирование выражений с членами, связанными рекуррентными соотношениями

Данный метод предложен Clenshaw для вычисления сумм вида

где функции F_k(x) связаны рекуррентным соотношением

для некоторых функций α(n,x) и β(n,x).

Определим вспомогательные переменные y_k следующими соотношениями:

Если разрешить эту систему относительно c_k, и подставить полученные выражения в исходную формулу для f(x), то после сокращения получим:

Числовой пример

Вычисление синуса на интервале [-1,1]

Вычисление синуса произвольного угла можно свести к вычислению синуса угла в интервале по формуле

делая замену переменных мы сведем диапазон значний аргумента к интервалу [-1,1].

При совершении данных операций возникает ошибка округления, но она оказывается существенно меньше ошибки ограничения. Проиллюстрируем это на примере.

Возьмем в качестве приближения функции первые пять членов ряда Тэйлора:

Ошибка ограничения меньше первого отброшенного члена:

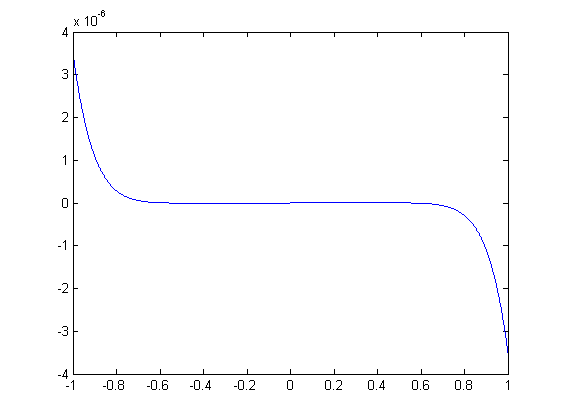
На рисунке изображен график абсолютной ошибки при вычислении по указанной формуле. Ошибка составляется из ошибки ограничения и ошибки округления, но в данном случае ошибка округления мала, по сравнению с ошибкой ограничения. Стоит отметить, что хотя ошибка практичски отсутствует вблизи нуля, она становится довольно большой при подходе к границам интервала.

При приближении той же функции полиномами Чебышева до 9 порядка получаем следующую формулу:

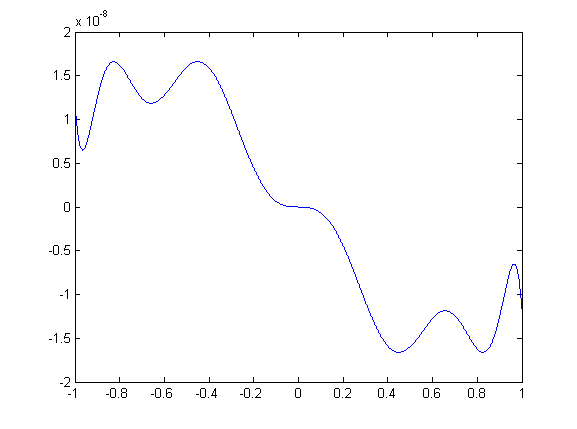
Метод экономизации можно применять не только для распространения максимальной ошибки ограничения по всему интервалу за счет уменьшения слагаемых в сумме, но и для уменьшения абсолютной величины ошибки, при неизменном количестве слагаемых.

После корректировки коэффициентов ряда Тэйлора с помощью метода экономизации получим:

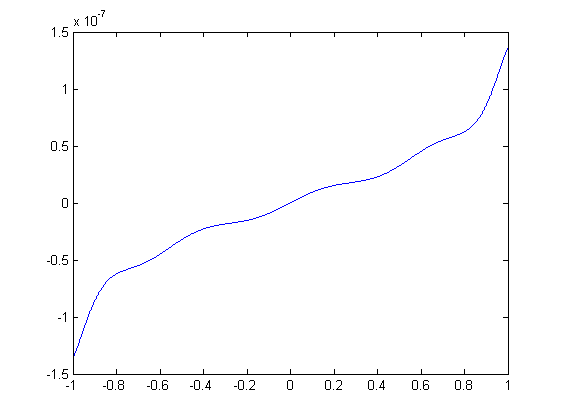
На следующем изображении представлены графики всех трех приближений и график функции , значения приближенний увеличены в каждой точке пропорционально абсолютной ошибке. Имеет смысл сравнивать график для конкретного приближения с графиком синуса, но не между собой, так как порядок ошибок в каждом случае разный.

Источник

Как решать задачи на функцию

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

1. Вычислить « y » при « x = 15 »
2. Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный .

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.

Теперь разделим и левую, и правую часть на « 2 », чтобы найти « x » .

Как проверить верно ли равенство для функции

Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».

Верно ли равенство « f(−2) = −18 »?

Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.

Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.

Не забывайте использовать правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили « f(−2) = 12 ».

Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию « y = x 2 −5x + 6 »

Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2) .

Для этой задачи нет необходимости, строить график заданной функции.

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).

Если получится верное равенство , значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию « y = x 2 − 5x + 6 » координаты точки (1; 2) .

Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».

У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1) . Принадлежит ли она
функции « y = x 2 − 5x + 6 »?

Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».

В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.

Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.

Найдем на графике функции « y(x) = −2x + 1 », чему равен « y » при x = 2 .

Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».

Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».

Для этого мы подставим x = 2 в формулу функции « y(x) = −2x + 1 ». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3 .

При расчетах мы также получили y = −3 .

Значит, мы правильно получили координаты с графика функции.

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.

При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Источник

Функция. Способы задания функций.

Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.

Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.

2. Графический способ заключается в проведении линии (графика), у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.

Например: для нахождения по графику у, которому соответствует х = 2,5 необходимо провести перпендикуляр к оси х на отметке 2,5. Отметку можно довольно точно сделать с помощью линейки. Тогда найдем, что при х = 2,5 у равно 7,5, однако если нам необходимо найти значение у при х равном 2,76, то графический способ задания функции не будет достаточно точным, т.к. линейка не дает возможности для столь точного замера.

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

Функцию можно задать с помощью математической формулы y=x 2 , тогда если х равно 2, то у равно 4, возводим х в квадрат.

4. Словесный способ состоит в задании функции обычным языком, т.е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.

Словесно можно задать функцию (задачу), принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.

5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.

При разложении числа Эйлера задается функцией:

Ее сокращение приведено ниже:

При прямом расчёте возникает бесконечная рекурсия, но можно доказать, что значение f(n) при возрастании n стремится к единице (поэтому, несмотря на бесконечность ряда, значение числа Эйлера конечно). Для приближённого вычисления значения e достаточно искусственно ограничить глубину рекурсии некоторым наперёд заданным числом и по достижении его использовать вместо f(n) единицу.

Источник