- Как найти площадь прямоугольника – 9 способов с формулами и примерами
- По диагонали и стороне
- По стороне и диаметру описанной окружности
- По радиусу описанной окружности и стороне
- По стороне и периметру – 1 способ
- По стороне и периметру – 2 способ
- По диагонали и углу между диагоналями
- По радиусу описанной окружности и углу между диагоналями – первый способ
- По радиусу описанной окружности и углу между диагоналями – второй способ
- Площадь прямоугольника — основные способы, правила и формулы вычислений
- Общие сведения
- Площадь фигуры
- Единицы измерения
- Информация о прямоугольнике
- Свойства и признаки
- Периметр и размерность
- Примеры решения
- Геометрия на плоскости
Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
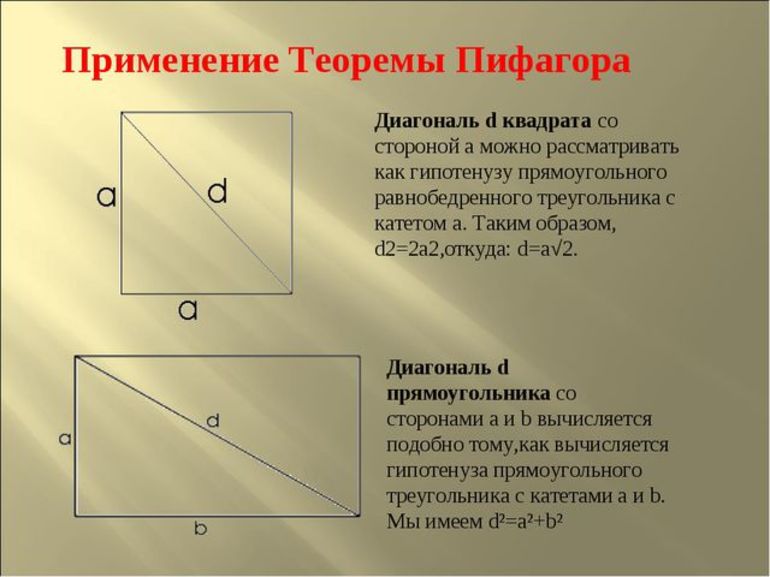
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
По стороне и периметру – 2 способ
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Источник
Площадь прямоугольника — основные способы, правила и формулы вычислений
Общие сведения
В различных задачах с физико-математическим уклоном приходится вычислять площадь прямоугольника. Однако формула расчета применяется не только в математике и физике, но и во время ремонтных работ. Например, следует посчитать количество расходных материалов, которое зависит от квадратуры комнаты или здания.
Очень важно не только знать основные соотношения, но и корректно переводить единицы измерения из одной в другую. От знаний полностью зависит экономия денежных средств. Например, при клейке обоев в комнате требуется определенное количество рулонов. Это количество можно купить в строительном магазине «на глаз» или рассчитать квадратуру комнаты. Во втором случае можно существенно сэкономить. Для того чтобы посчитать квадратные метры помещения, нужно вычислить его площадь.
Площадь фигуры
Площадью двумерной фигуры является численная характеристика, которая показывает ее размерность. Она обозначается литерой S и измеряется в квадратных единицах (мм 2 , см 2 , дм 2 и т. д.). Не каждый элемент геометрии имеет площадь. Прямая, луч, отрезок, точка не имеют двумерной размерности. Фигуры, у которых она присутствует, являются квадратируемыми. Если значения их S равны, то они являются равновеликими.
Для вычисления значения двухплоскостной размерности фигуры применяется интегральный метод. Однако бывают частные случаи, когда вычислять интеграл необязательно. Существуют определенные формулы, полученные с помощью интегрального метода. Чтобы ими воспользоваться, нужно просто подставить числовые значения сторон.
Нахождение площади получило широкое распространение в физике. Например, для вычисления электрического сопротивления нужно найти площадь поперечного сечения проводника. Она зависит от его формы. Площадь можно вычислить и у объемной поверхности, но для этого применяется интегрирование.
Единицы измерения
При решении задач на нахождение значения площади нужно знать единицы ее измерения. Кроме того, следует правильно выполнять перевод одной единицы в другую. В системе исчисления используются квадратичные единицы измерения. За основу следует брать размер стороны прямоугольника. Например, при указании площади в кв. м нужно измерять в метраже стороны объекта. Это стандартная единица измерения площади.
Существуют также производные единицы. Самой маленькой из них является квадратный миллиметр (кв. мм или мм 2 ). В некоторой литературе или программировании можно встретить такую запись: sqr (m), которая означает квадратный метр. Основные производные единицы площади:
1 см 2 = 100 мм 2 .
1 дм 2 = 100 см 2 .
1 м 2 = 100 дм 2 = 10000 см 2 .
1 км 2 = 1000000 м 2 .
1 ар (а) = 1 сотка = 100 м 2 .
1 гектар (га) = 10000 м 2 .
Последние применяются для измерения земельного участка. Однако необязательно их все помнить. Они легко выводятся при помощи простейших математических вычислений. Например, для выполнения расчетов нужно перевести кв. м в кв. см. Однако человек мог забыть, сколько см 2 в квадратном метре. Следует взять метрическую форму (1 м = 100 см). Затем нужно возвести обе части выражения в квадрат: 1 м 2 = 100 * 100 = 10000 (см 2 ).
Информация о прямоугольнике
Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.
Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.
Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.
Свойства и признаки
Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:
- Условие параллельности и равенства противоположных сторон.
- Наличие четырех прямых углов.
- Равенство диагоналей.
- Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
- Все стороны не равны между собой.
Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:
- Углы равны между собой 90 градусов.
- Противолежащие параллельные стороны равны.
- Сумма всех внутренних углов составляет 360.
- Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
- Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
- Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
- Точка пересечения диагоналей — центр симметрии.
- Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.
Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.
Периметр и размерность
Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d 2 — 2a 2 )]^(1/2) и P = 2b + [2 * (2d 2 — 2b 2 )]^(1/2).
Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.
Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * [p * (p — a) * (p — b) * (p — d)]^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.
Примеры решения
Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:
- Две стороны.
- Одна из сторон и диагональ.
- Диагональ и разность сторон.
Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.
При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.
Геометрия на плоскости
Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2 ). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.
Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:
Находится неизвестная сторона: b =(d 2 — a 2 )^(1/2) = (100 — 36)^(1/2) = 8 (м).
Площадь (произведение сторон): S = 6 * 8 = 48 (м 2 ).
Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:
Значение площади будет вычисляться таким образом: S = 2 * [12 * (12−6) * (12−8) * (12−10)]^(1/2) = 2 * 24 = 48 (м 2 ).
Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:
- Обозначить стороны: a = x и b = x — 3.
- Составить уравнение: x * (x — 3) = 10.
Раскрыть скобки: x 2 — 3x — 10 = 0.
Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) 2 ). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.
Таким образом, для расчета площади прямоугольника можно воспользоваться формулой, а не выполнять интегрирование. Однако перед этим нужно внимательно изучить основные понятия и математические отношения.
Источник