Все способы умножения примеры

Виды умножения

проблема : разобраться видах умножения

Цель:ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи:
1. Найти и разобрать различные способы умножения.
2. Научиться демонстрировать некоторые способы умножения.
3. Рассказать о новых способах умножения и научить ими пользоваться учащихся.
4. Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.
5. Эксперимент «какой способ быстрей»
Гипотеза:Надо ли знать таблицу умножения?
Актуальность:В последнее время ученики доверяют гаджетам больше чем себе. И по этому считают только на калькуляторах. Мы хотели показать что есть разные способы умножение, что бы ученикам было легче считать,и интересно учить.
ВВЕДЕНИЕ
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.
В разное время разные народы владели разными способами умножения натуральных чисел.
Почему же сейчас все народы применяют один способ умножения «столбиком»?
Почему люди отказались от старых способов умножения в пользу современного?
Имеют ли забытые способы умножения право на существование в наше время?
Что бы ответить на эти вопросы я проделал следующую работу:
1. С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;
2. Изучил литературу, предложенную учителем;
3. Решил пару примеров всеми изученными способами, что бы узнать их недостатки;
4) Выявил среди них наиболее эффективные;
5. Провел эксперимент;
6. Сделал выводы.
1. Найти и разобрать различные способы умножения.
Умножение на пальцах.

Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.

Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.

Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.

Способы умножения чисел в разных странах

Умножение на 9.

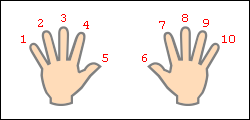
Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

Кто придумал умножение на пальцах

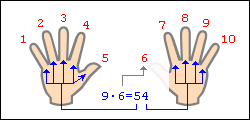
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».

Умножение необычным способом

Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.

7 клеток 2 клетки.

Индийский способ умножения.

Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.

Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:

(300 + 3 ∙ 6 = 318) 318

(3180 +7 ∙ 6 = 3222) 3222

6
Умножение способом «МАЛЕНЬКИЙ ЗАМОК».

Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.

За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».

Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.

Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.

Способы умножения чисел в разных странах

Умножение чисел методом «ревность».

«Методы умножения Второй способ носит романтическое название ревность», или «решётчатое умножение».

Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».

Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.

В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.

Крестьянский способ умножения.

Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.

В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением

Произведение всех пар соответственных чисел одинаковое, поэтому

37 ∙ 32 = 1184 ∙ 1 = 1184

В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:

24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408
Новый способ умножения.

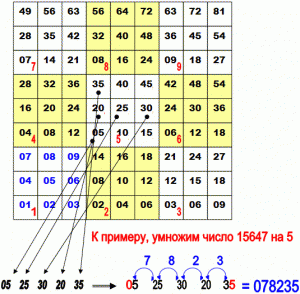
Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.

Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35

Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.

В итоге получаем: 078235. Число 78235 и есть результат умножения.

Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

Умножение графическим методом (линейным, китайским)

Перемножим два двузначных числа: 15*23

Шаг 1. первое число 15:

Рисуем первую цифру – одной линией.

Рисуем вторую цифру – пятью линиями.

Шаг 2. второе число 23:

Рисуем первую цифру – двумя линиями.

Рисуем вторую цифру – тремя линиями.

Шаг 3.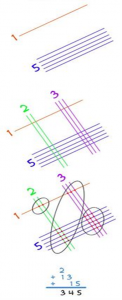 Подсчитываем количество точек в группах.

Шаг 4. Результат – 345

Проведем эксперимент

С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом.

Заключение.

Работая над этой темой, я узнал, что существует порядка 30 различных, забавных и интересных способов умножения. Некоторыми в различных странах пользуются до сих пор. Я выбрал для себя некоторые интересные способы. Но не все способы удобны в использовании, особенно при умножении многозначных чисел.

Источник

Учим таблицу умножения: 9 эффективных способов

Таблица умножения дается некоторым детям нелегко, особенно если у ребёнка плохая память . Порой бывает недостаточно применять простое заучивание надоевших, и никак не укладывающихся в голове, столбцов. Можно облегчить ребёнку процесс запоминания таблицы умножения, если знать несколько несложных, но очень действенных приёмов.

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32.

Совет № 2

Умножать можно с помощью рук

Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

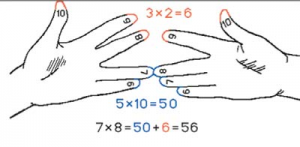
Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

• При умножении любого числа на 1 получается то число, которое умножали.
• Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
• Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
• Чтобы умножать на 4 , можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
• При умножении на 9 , запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.

Совет №4

Научиться пользоваться таблицей Пифагора

Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.

Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).

Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.

Нестандартные методы запоминания таблицы умножения

Совет №5

Использовать шифровки, раскраски, лабиринты…

Подобные задания увлекают ребёнка и облегчают запоминание таблицы умножения.

Шифровки

Раскраски

Лабиринты

Но так же очень полезно детям проходить и обычные лабиринты, соответствующие возрасту.

Тренажер по таблице умножения и деления

Бесценный богатый тренажер!
В книге вы найдете:

• 110 страниц интересных результативных упражнений;
• разнообразные задания;
• творческий подход;
• нестандартные приемы;
• задания разного уровня сложности;
• различные шифровки;
• игры и раскраски.

Ваш ребенок получит:

• легкое и без нервов запоминание таблицы умножения;
• развитие внимания и мышления;
• улучшение в целом математических способностей;
• огромное количество интересных и полезных заданий.

Книга может быть использована как для индивидуальной работы, так и работы в классе.
Скучно точно не будет!

Тренажер удобен для распечатывания!

Совет №6

Можно ли выучить таблицу умножения быстро и легко наизусть в игровой форме? Оказывается да!

Нужно просто играть с ребёнком в игры, где необходимо знание таблицы умножения. И сейчас мы такие игры разберем.

Игра 1

Можно приготовить карточки со случаями умножения без ответов. Ребёнок должен вытягивать по одной. Если он даёт правильный ответ, то откладывает карточку в сторону, неправильный — возвращает в стопку. Можно устроить соревнования: кто больше даст правильных ответов.

Игру можно разнообразить. Например, давать ответы на время. И каждый день подсчитывать количество правильных ответов, чтобы у ребёнка появилось желание улучшить свой вчерашний рекорд. Можно вместо карточек с выражениями подготовить карточки с ответами. Например, на карточке написано число 24. Ребёнок должен назвать несколько случаев, в которых результатом умножения будет это число.

Игра 2

1. На игровом поле 100 квадратов с результатами умножения двух чисел, которые есть на игральных кубиках (от 1 до 6). Числа на поле повторяются!
2. Первый игрок бросает кубики и умножает выпавшие числа. Получившийся результат ищет на поле и рисует линию, соединяя любые две точки квадрата, внутри которого находится это число.
3. Второй игрок делает то же самое, и далее по очереди.
4. Когда игрок рисует линию, полностью закрывающую квадрат, он его закрашивает. Грани у квадрата могут быть нарисованы и соперником, главное — быть последним. После этого игрок, закрасивший квадрат, бросает кубики снова.
5. Побеждает игрок с наибольшим количеством закрашенных квадратов.

Совет №7

Для быстрого и легкого запоминания таблицы умножения можно сделать с ребёнком специальные браслеты.

Если поочередно носить такие браслеты на руке, то запоминание автоматически происходит быстрее, т.к. подключается зрительная память.

Совет №8

Математические фокусы

Чтобы выполнять математические фокусы , знание таблицы умножения просто необходимо. Поэтому, если вашего ребёнка увлечёт этот процесс и он захочет покорить сверстников своими тайными математическими знаниями, то таблицу умножения ребёнок точно выучит.

Совет №9

Стихи

Не нужно запоминать все стихотворные строчки. Достаточно выбрать только те моменты, которые ребёнку даются с трудом.

2 × 2 = 4
Два атлета взяли гири.
Это: дважды два — четыре.

2 × 3 = 6
Сел петух до зари
На высокий шест:
— Кукареку. Дважды три,
Дважды три — шесть!

2 × 4 = 8
В пирог вонзилась пара вилок:
Два на четыре — восемь дырок.

2 × 5 = 10
Двух слонов решили взвесить:
Дважды пять — получим десять.
То есть весит каждый слон
Приблизительно пять тонн.

2 × 6 = 12
Повстречался с раком краб:
Дважды шесть — двенадцать лап.

2 × 7 = 14
Дважды семь мышей —
Четырнадцать ушей!

2 × 8 = 16
Осьминоги шли купаться:
Дважды восемь ног — шестнадцать.

2 × 9 = 18
Вы видали подобное чудо?
Два горба на спине у верблюда!
Стали девять верблюдов считаться:
Дважды девять горбов — восемнадцать.

3 × 3 = 9
Кофе пили три букашки
И разбили по три чашки.
Что разбито, то не склеить…
Трижды три — выходит девять.

3 × 4 = 12
Целый день твердит в квартире
Говорящий какаду:
— Тррри умножить на четыррре,
Тррри умножить на четыррре —
Двенадцать месяцев в году.

3 × 5 = 15
Школьник стал писать в тетрадь:
Сколько будет «трижды пять»?
Был он страшно аккуратен:
Трижды пять — пятнадцать пятен!

3 × 6 = 18
Стал Фома оладьи есть:
Восемнадцать — трижды шесть.

3 × 7 = 21
Трижды семь — двадцать один:
На носу горячий блин.

3 × 8 = 24
Прогрызли мыши дыры в сыре:
Трижды восемь — двадцать четыре.

3 × 9 = 27
Трижды девять — двадцать семь.
Это нужно помнить всем.

4 × 4 = 16
Четыре милых свинки
Плясали без сапог:
Четырежды четыре — шестнадцать голых ног.

4 × 5 = 20
Четыре учёных мартышки
Ногами листали книжки.
На каждой ноге — пять пальцев:
Четырежды пять — двадцать.

4 × 6 = 24
Шла на парад
Картошка-в-мундире:
Четырежды шесть — двадцать четыре!

4 × 7 = 28
Цыплят считают под осень:
Четырежды семь — двадцать восемь!

4 × 9 = 36
У Бабы-яги сломалась ступа.
Четырежды восемь — тридцать два зуба!
Беж жубов ей нечем есть:
Четырежды девять — «тридцать шешть»!

5 × 5 = 25
Вышли зайцы погулять:
Пятью пять — двадцать пять.

5 × 6 = 30
Забежала в лес лисица:
Пятью шесть — выходит тридцать.

5 × 7 = 35
Пять медведей из берлоги
Шли по лесу без дороги —
За семь вёрст кисель хлебать:
Пятью семь — тридцать пять!

5 × 8 = 40
Влезть сороконожке
Трудно на пригорок:
Утомились ножки —
Пятью восемь — сорок.

Встали пушки на пригорок:
Пятью восемь — вышло сорок.

5 × 9 = 45
Пушки начали стрелять:
Пятью девять — сорок пять.

Если лаптем щи хлебать:
Пятью девять — сорок пять.
Будет этот лапоть
Всем на брюки капать!

6 × 6 = 36
Шесть старушек пряли шерсть:
Шестью шесть — тридцать шесть.

6 × 7 = 42
Шесть сетей по шесть ершей —
Это тоже тридцать шесть.
А попалась в сеть плотва:
Шестью семь — сорок два.

6 × 8 = 48
Бегемоты булок просят:
Шестью восемь — сорок восемь.

6 × 9 = 54
Нам не жалко булок —
Рот откройте шире:
Шестью девять будет
Пятьдесят четыре.

7 × 7 = 49
Дураков не жнут, не сеют,
Сами нарождаются:
Семью семь — сорок девять…
Пусть не обижаются!

7 × 8 = 56
Раз олень спросил у лося:
«Сколько будет семью восемь?»
Лось не стал в учебник лезть:
«Пятьдесят, конечно, шесть!»

7 × 9 = 63
У семи матрёшек
Вся семья внутри:
Семью девять крошек —
Шестьдесят три.

8 × 8 = 64
Пылесосит носом
Слон ковры в квартире:
Восемь на восемь —
Шестьдесят четыре.

8 × 9 = 72
Восемь медведей рубили дрова:
Восемью девять — семьдесят два.

8 × 10 = 80
Самый лучший в мире счёт:
Наступает Новый год!
В восемь рядов игрушки висят:
Восемью десять — восемьдесят!

9 × 9 = 81
Свинка свинёнка решила проверить:
— Сколько получится «девять на девять»?
— Восемьдесят — хрю — один! —
Так ответил юный свин.

Если ребёнок будет выполнять задания с интересом, понимать то, что он делает, то результат по запоминанию таблицы умножения будет достигнут гораздо быстрее. Желаю удачи и очень рекомендую дать ребенку возможность выучить таблицу умножения быстро и с интересом.

С уважением, Ольга Наумова

Заходите в Книжную лавку за полезными книгами!

Благодарю, что поделились статьей в социальных сетях!

Источник