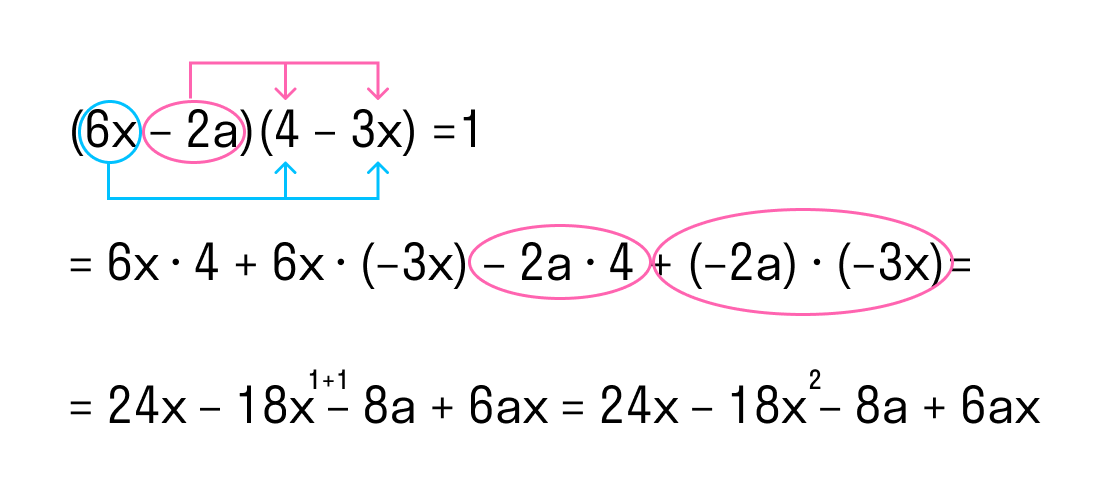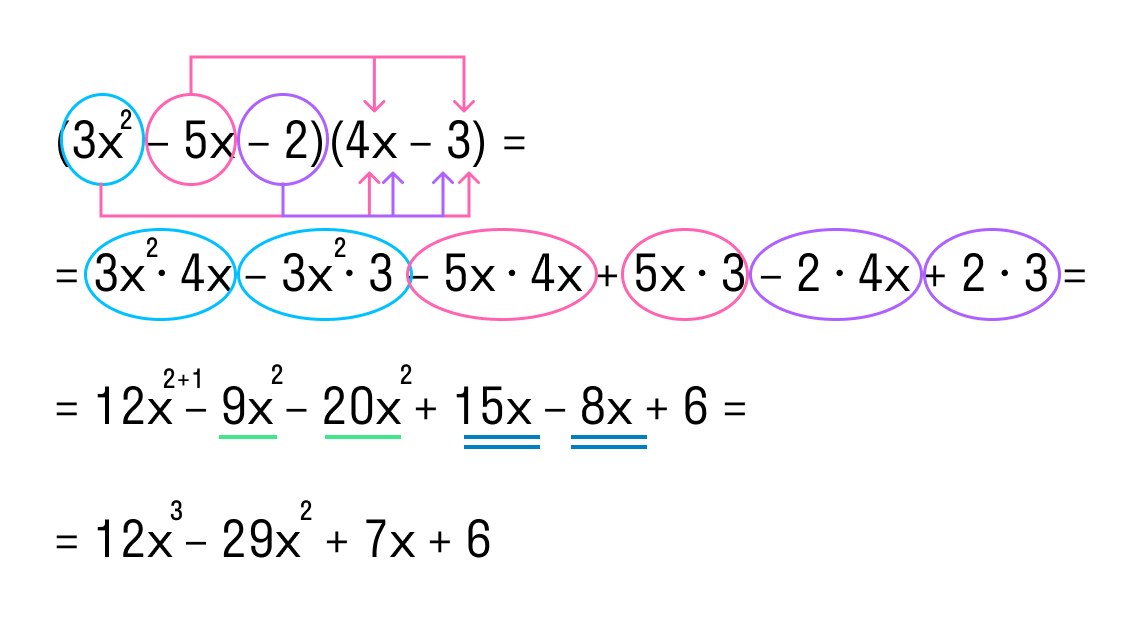Все способы умножения многочленов

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Упрощение многочлена.
Умножение многочленов.

С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень

Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.

Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Произведение одночлена и многочлена. Понятие многочлена

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\( 5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\( xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Например, многочлен
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.

Представим все слагаемые в виде одночленов стандартного вида:
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\( = 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)

Приведем в полученном многочлене подобные члены:
\( 8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида.

За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен \( 12a^2b — 7b \) имеет третью степень, а трехчлен \( 2b^2 -7b + 6 \) — вторую.

Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
\( 5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\( 9a^2b(7a^2 — 5ab — 4b^2) = \)
\( = 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\( = 63a^4b — 45a^3b^2 — 36a^2b^3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \( (a + b)^2, \; (a — b)^2 \) и \( a^2 — b^2 \), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, \( (a + b)^2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.

Выражения \( (a + b)^2, \; (a — b)^2 \) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
\( (a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = \)
\( = a^2 + 2ab + b^2 \)

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

\( (a + b)^2 = a^2 + b^2 + 2ab \) — квадрат суммы равен сумме квадратов и удвоенного произведения.

\( (a — b)^2 = a^2 + b^2 — 2ab \) — квадрат разности равен сумме квадратов без удвоенного произведения.

\( a^2 — b^2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Источник

Действия с многочленами

Мы уже разобрали, что из себя представляют многочлены. В рамках данной статьи мы расскажем, как правильно вычитать, умножать, складывать и делить подобные выражения, а также как возводить их в натуральную степень, т.е. определим правила совершения данных действий с многочленами.

Правила сложения и вычитания многочленов

Складывать и вычитать многочлены достаточно просто. Оба эти действия рассматриваются вместе, поскольку осуществляются по одним и тем же принципам:

1. Начинаем с правильной записи суммы или разности исходных многочленов. Для этого их надо заключить в скобки и поместить между ними нужный знак.
2. Далее выполняем раскрытие скобок и получаем новый многочлен.
3. После этого нужно привести многочлен к стандартному виду (если это необходимо).

Поясним алгоритм примером.

Условие: выполните сложение и вычитание двух многочленов x · y − x 2 + 2 и 7 · x 2 − 1 .

Сначала выполним сложение. Записываем сумму:

( 7 · x 2 − 1 ) + ( x · y − x 2 + 2 )

Раскрываем скобки и получаем новый многочлен в следующей форме:

7 · x 2 − 1 + x · y − x 2 + 2

Нам осталось только привести результат к стандартному виду:

7 · x 2 − 1 + x · y − x 2 + 2 = 6 · x 2 + 1 + x · y

Далее проводим вычитание по аналогии со сложением:

( 7 · x 2 − 1 ) − ( x · y − x 2 + 2 ) = 7 · x 2 − 1 − x · y + x 2 − 2 = 8 · x 2 − 3 − x · y

Ответ: ( 7 · x 2 − 1 ) + ( x · y − x 2 + 2 ) = 6 · x 2 + 1 + x · y и ( 7 · x 2 − 1 ) − ( x · y − x 2 + 2 ) = 8 · x 2 − 3 − x · y .

Другие примеры вы можете найти в отдельной статье, посвященной сложению и вычитанию многочленов.

Правила умножения одного многочлена на другой

Перейдем к рассмотрению следующего действия – умножения. Основное правило его выполнения основано на распределительном свойстве умножения. С его помощью мы можем свести умножение многочленов к последовательному перемножению всех их членов друг на друга. Запишем правило:

Чтобы умножить один многочлен на другой, необходимо выполнить умножение каждого члена первого множителя на каждый член второго множителя, после чего провести сложение итоговых произведений.

Результатом умножения двух многочленов друг на друга будет новый многочлен.

Условие: выполните умножение двух многочленов a − b и − 3 · a + b .

Начнем с записи произведения.

( a − b ) · ( − 3 · a + b )

После этого нам нужно взять первый член первого многочлена (т.е. a ) и перемножить его с каждым членом второго многочлена. У нас получится a · ( − 3 · a ) и a · b . То же самое проделаем и со вторым членом. В итоге мы пришли к произведениям − b · ( − 3 · a ) и − b · b . Теперь складываем все, что у нас получилось:

a · ( − 3 · a ) + a · b − b · ( − 3 · a ) − b · b = − 3 · a 2 + 4 · a · b − b 2

Вот запись всего решения:

( a − b ) · ( − 3 · a + b ) = = a · ( − 3 · a ) + a · b − b · ( − 3 · a ) − b · b = = − 3 · a 2 + 4 · a · b − b 2

Ответ: ( a − b ) · ( − 3 · a + b ) = − 3 · a 2 + 4 · a · b − b 2 .

Мы также можем выполнить умножение многочлена на одночлен. Это можно рассматривать как частный случай умножения, приведенного выше. Советуем прочесть отдельную статью об умножении многочленов, где представлены более подробные теоретические положения и приведены более сложные примеры.

Правила возведения многочлена в степень

После того, как мы разобрались с правилами умножения многочленов, можем перейти к возведению в натуральную степень. Это действие может быть приравнено к умножению имеющегося многочлена на аналогичный столько раз, сколько написано в показателе. Так, возведению 3 · x + 1 в степень 4 мы можем поставить в соответствие произведение 4 -х многочленов: ( 3 · x + 1 ) · ( 3 · x + 1 ) · ( 3 · x + 1 ) · ( 3 · x + 1 ) .

Условие: выполните возведение многочлена 2 · a · b − b 3 в квадрат.

представим эту степень как произведение двух одинаковых множителей и вычислим нужный результат.

( 2 · a · b − b 3 ) 2 = = ( 2 · a · b − b 3 ) · ( 2 · a · b − b 3 ) = = 2 · a · b · ( 2 · a · b ) + 2 · a · b · ( − b 3 ) − b 3 · ( 2 · a · b ) − b 3 · ( − b 3 ) = = 4 · a 2 · b 2 − 4 · a · b 4 + b 6

Ответ: ( 2 · a · b − b 3 ) 2 = 4 · a 2 · b 2 − 4 · a · b 4 + b 6 .

Подводя итог этого пункта, отметим, что возведение в степень можно выполнять намного быстрее, если пользоваться формулами сокращенного умножения. Советуем вам изучить эту тему более подробно.

Правила деления многочлена на многочлен

Мы уже выяснили, что результатом всех рассмотренных действий является новый многочлен. Действие деления отличается от них тем, что чаще всего его результат не будет многочленом. Так, если мы разделим x · y − 1 на x 2 + y 2 , то в итоге у нас получится дробь x · y — 1 x 2 + y 2 .

Однако в принципе получить в результате многочлен можно, например, здесь: ( x 2 · y + x · y 2 − x + x · y + y 2 − 1 ) : ( x + 1 ) = x · y + y 2 − 1 . В таких случаях мы можем говорить о делимости одного многочлена на другой, так же, как мы отмечали это для целых чисел. Тогда при делении нам нужно представить делимый многочлен в виде произведения двух многочленов — делителя и частного от деления. Во взятом нами примере делимое x 2 · y + x · y 2 − x + x · y + y 2 − 1 рассматривается как произведение ( x + 1 ) · ( x · y + y 2 − 1 ) .

Если у обоих многочленов есть только одна переменная, то тогда речь идет о делении без остатка. Сформулируем правило для многочлена, включающего в себя одну действительную переменную x . Обозначим данный многочлен P ( x ) .

Деление многочлена P ( x ) на другой многочлен M ( x ) , без остатка происходит тогда, когда есть другой многочлен Q ( x ) , удовлетворяющий условию P ( x ) = M ( x ) · Q ( x ) .

Так, мы можем разделить x 3 + 2 · x 2 + 3 · x + 6 на x + 2 без остатка в силу существования многочлена x 2 + 3 . Тогда равенство x 3 + 2 · x 2 + 3 · x + 6 = ( x + 2 ) · ( x 2 + 3 ) будет справедливым.

А вот x 2 + 1 поделить на x 3 − 5 без остатка мы не сможем, поскольку нет такого Q ( x ) , которое подошло бы для равенства x 2 + 1 = ( x 3 − 5 ) · Q ( x ) .

Деление без остатка есть частный случай деления с остатком, ведь при нем мы также получаем остаток, равный 0 . В общем случае можно сказать, что когда мы делим многочлен P ( x ) степени n , которая будет больше единицы, на другой многочлен Q ( x ) степени k (причем 1 ≤ k ≤ n ), мы получаем в итоге новый многочлен M ( x ) степени n − k и остаток в виде многочлена R ( x ) , степень которого будет меньше, чем k . Представим данное утверждение как теорему.

Мы можем представить любой многочлен P ( x ) степени n ( n ≥ 1 ) как P ( x ) = M ( x ) · Q ( x ) + R ( x ) . Здесь Q ( x ) будет некоторым многочленом степени k ( 1 ≤ k ≤ n ) , M ( x ) – многочленом степени n − k и R ( x ) – многочленом степени, меньшей k . Это представление будет единственным.

Под Q ( x ) , M ( x ) и R ( x ) в данном случае понимается любой многочлен из множества тождественно равных многочленов.

Так, если мы делим 3 · x 4 + 2 · x 2 − 1 на x 2 + x , то у нас получится частное 3 · x 2 − 3 · x + 5 с остатком − 5 · x − 1 .

Это так, потому что равенство 3 · x 4 + 2 · x 2 − 1 = ( x 2 + x ) · ( 3 · x 2 − 3 · x + 5 ) − 5 · x − 1 является справедливым. Его справедливость легко проверить, выполнив все нужные действия с правой стороны.

Если мы делим P ( x ) на Q ( x ) , причем степень делимого будет больше степени делителя, то в итоге мы всегда получаем частное в виде нулевого многочлена и остаток, равный делимому. Так, разделив x 2 + 1 на x 3 + 2 · x 2 − 1 , мы получим нулевое частное и остаток x 2 + 1 .

Удобно производить деление, предварительно сделав запись уголком, так же, как мы делаем это для целых чисел. Подробнее это действие разобрано в статье, посвященной делению многочлена на многочлен.

Источник

Умножение многочлена на многочлен

О чем эта статья:

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

1. Привести к стандартному виду все одночлены, которые входят в многочлен.
2. Привести подобные члены.

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

Правило умножения двучленов:

(a + b) * (c + d) = ac + ad + bc + bd.

Правило умножения двучлена на трехчлен:

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

Правило перемножения трехчленов:

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

• Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
• Сначала составим их произведение: (a + b)(c + d).
• Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
• Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
• Проведем обратную замену x на (c + d):
  a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
• Как изменилось произведение исходных многочленов:
  (a + b)(c + d) = ac + ad + bc + bd.
  Как раз так и выглядит формула умножения многочлена на многочлен.

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

1. Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.
2. Сложить полученные произведения.
3. Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

• Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
• Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

• Умножим первый многочлен на второй. Результат запишем в скобках.
  
• Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.
  

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x 2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x 2 , 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx 2 , −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1 = 2x 2 − 14 x + 2 − 3x 3 + 21x 2 − 3x = (2x 2 + 21x 2 ) + (−14x − 3x) + 2 − 3x 3 = 23x 2 − 17x + 2 − 3x 3 .

Получается, что (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Ответ: (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Источник