Математика. 6 класс
Конспект урока
Сложение целых чисел (продолжение)
Перечень рассматриваемых вопросов:
- Рассмотреть правило сложения нескольких целых чисел.
- Рассмотреть задачи с практическим содержанием.
- Обобщить и систематизировать знания и умения по теме «Сложение целых чисел».
Чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых.
Чтобы сложить числа разных знаков, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.
Чтобы сложить несколько целых чисел, нужно сначала складывать числа с одинаковыми знаками по правилу сложения чисел с одинаковыми знаками, а затем, используя правило сложения чисел с разными знаками, получить окончательный результат
Для упрощения записи суммы у положительных слагаемых обычно знак «+» и скобки опускают.
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258с.
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Сегодня мы продолжаем рассматривать сложение положительных и отрицательных целых чисел.
Вспомним, как складывают два числа с одинаковыми знаками.
Чтобы сложить два числа с одинаковыми знаками, надо сложить их модули и поставить перед суммой знак слагаемых.
Вспомним, как складывают два числа с разными знаками.
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.
Бывают случаи, когда нужно сложить несколько чисел.
Утром температура была (– 10 o С), днём она повысилась на 13 о С, а вечером снова опустилась на 7 o С. Узнаем, чему равна температура воздуха вечером.
(– 10) + (+ 13) + (– 7) = – (10 + 7) + (+ 13) = (– 17) + 13 = – 4
Значит, вечером термометр покажет температуру (– 4 о С).
Итак, сформулируем правило сложения нескольких целых чисел.
Чтобы сложить несколько целых чисел, нужно сначала складывать числа с одинаковыми знаками, по правилу сложения чисел с одинаковыми знаками, а затем, используя правило сложения чисел с разными знаками, получить окончательный результат.
Таким образом, на этом уроке мы вспомнили правила сложения для чисел с одинаковыми и разными знаками.
Узнали, как складывать несколько целых чисел, и научились решать задачи, используя эти правила.
Рассмотрим несколько задач.
В какой из дней недели температура днём была больше?
В понедельник утром температура была равна (– 2 o С), а днём повысилась на 5 o С.
Во вторник утром температура была равна (– 4 o С), а днём повысилась на 6 o С.
Температура днём в понедельник:
Температура днём во вторник:
Значит, температура днём в понедельник была больше, чем во вторник.
Ответ: в понедельник.
Бензин замерзает при температуре (– 72 o С). Если уменьшить эту температуру на 28 o С и к разности прибавить (– 17 o С), то получим температуру замерзания спирта. Определите её.
(– 72) + (– 28) + (– 17) = – (72 + 28) – 17 = – 100 – 17 = – 117
Получили, что температура замерзания спирта (– 117 o С).
1. Разместите нужные подписи под изображениями
Какие значения показывают термометры?
Рис. 1 – Положительное число
Рис. 2 – Отрицательное число
2. Вставьте в текст нужные слова
Чтобы …несколько целых чисел, нужно сначала… числа с…знаками, по правилу сложения чисел с одинаковыми…, а затем, используя правило сложения чисел с …знаками, получить окончательный результат.
Варианты слов для вставки:
Чтобы сложить несколько целых чисел, нужно сначала складывать числа с одинаковыми знаками, по правилу сложения чисел с одинаковыми знаками, а затем, используя правило сложения чисел с разными знаками, получить окончательный результат.
Источник
Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
Значение данного выражения равно 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
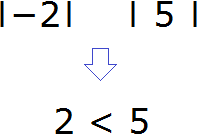
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2 .
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) в ычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
Заменим вычитание сложением:
Дальнейшее вычисление не составляет труда:
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Источник