Все способы рисования пирамиды

Перспектива Пирамида. Урок 3

Давайте построим еще одну геометрическую фигуру — пирамиду.
С этой фигурой у нас особые ассоциации: МММ, Мавроди, денежная пирамида, кидалово и т. д. Но об этом в других уроках.
А этот урок подойдет для любителей египетской тематики. Пирамиды Египта, Хеопс, сфинкс, жрецы, храм — все это завораживает. Кстати, будь то гробница фараона или сфинкс, все равно придется применять законы перспективы, чтобы рисунки получались.

Традиционно это простая фигура, и построение ее так же простое, как и куб, как и цилиндр.

Пирамида — рисунок в картинках

Опять же присутствует линия горизонта, без нее ни как, поэтому рисуем. Линия горизонта всегда находится на уровне глаз художника. На предметы выше этой линии художник смотрит снизу, на предметы ниже этой линии художник смотрит сверху. В данном уроке предмет у нас будет ниже линии горизонта, поэтому мы на него смотрим сверху. Все картинки кликабельны:

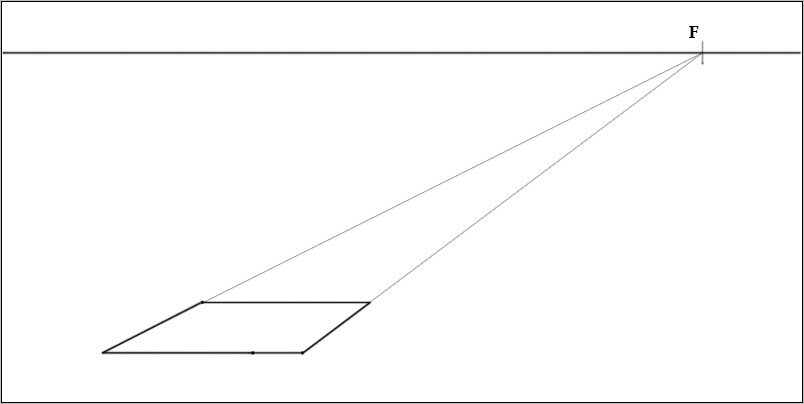
Далее произвольно, или нужного нам размера, рисуется прямая линия . Смотрим в низ на рисунок :

Теперь на линии горизонта выбираем точку схода F, и проводим прямые линии ( линии схода ) к нашему отрезку. Рисунок ниже:

Дальше проводим заднюю линию, нашей будущей пирамиды, и соединяем наш четырехугольник вместе, как показано на рисунке внизу и у нас получится основание пирамиды:

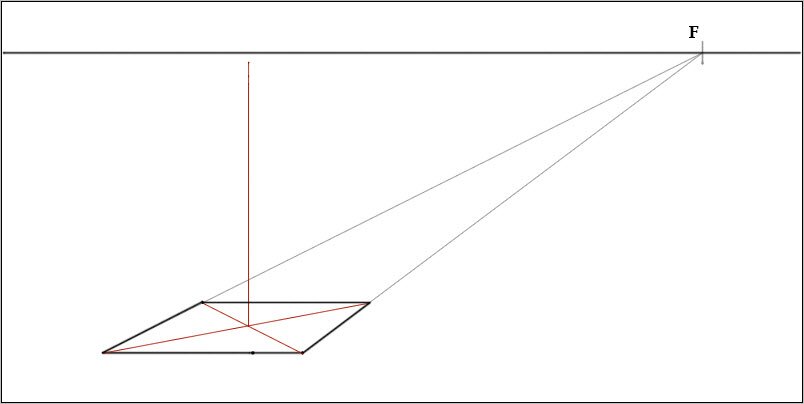
Ищем центр нашего четырехугольника. Для этого проводим прямые линии по диагонали в углы пирамиды. На рисунке внизу они выделенные красным цветом:

Из центра основания пирамиды проводим ось вверх до нужной нам высоты. Смотрим на рисунок внизу:

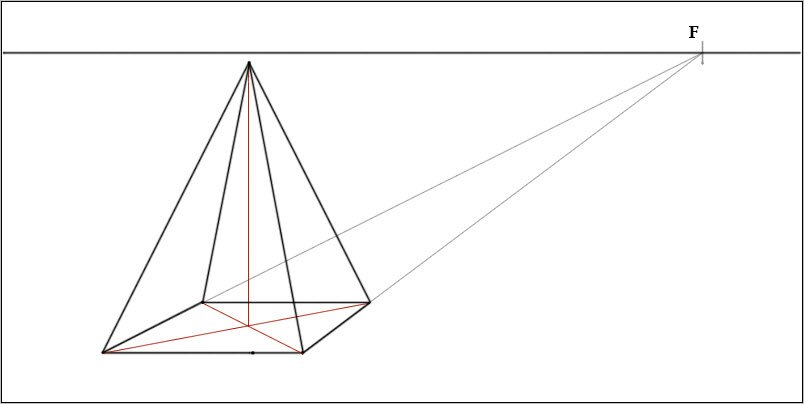
И теперь от верха оси рисуем прямые к углам нашей пирамиды:

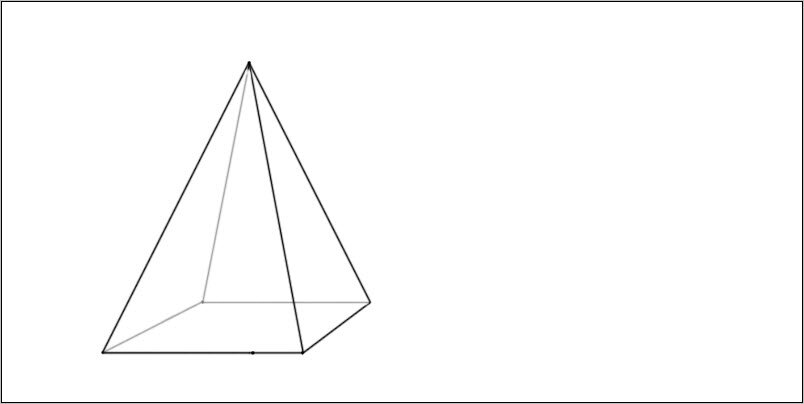
Чтобы закончить построение, убираем все вспомогательные линии. И для наглядности можем задние линии, и заднее ребро пирамиды сделать менее жирными, это даст эффект прозрачности у нас призма получится:

Это урок получился еще проще чем куб. Ну вообще то, если понять принцип построения перспективы, то все уроки окажутся легкими, и вы на 60% можете считать себя художником, и эти картины или рисунок букета цветов нам уже по зубам (я так думаю). Успехов.

Источник

Как нарисовать пирамиду?

Пирамиды остаются одними из самых популярных туристических объектов. Они поражают своим величием. Идеально ровные линии и углы заставляют усомниться в том, что такое сооружение могло быть создано руками человека.

Пирамиды часто появляются на картинах художников. Мы рассмотрим, как нарисовать пирамиду правильно, чтобы рисунок выглядел ровным и аккуратным.

Пирамида — элемент, который обязательно разбирают при изучении академического рисунка. Эта геометрическая фигура простая, но при этом требует определенных навыков и умений, развитого пространственного мышления. Разберем несколько способов рисунка правильной четырехугольной пирамиды.

Для работы сегодня нам понадобятся следующие материалы:

• простой карандаш или линер, работайте теми материалом, который лучше знаком.
• ластик;
• бумага.

В процессе работы стоит помнить о важных правилах:

• начинать работу следует легко, без нажима карандаша;
• линии должны быть четкими, стоит избегать “мохнатых” линий, так как это будет мешать нахождению точек пересечения;
• подкладывайте под руку чистый лист, чтобы избежать замазывания рисунка.

Как нарисовать классическую пирамиду карандашом?

Рассмотрим один из самых простых и стандартных вариантов рисунка пирамиды.

Рисуем равнобедренный треугольник. Учитесь рисовать без линейки, в рисунке все линии должны быть живыми. Это развивает руку, делает её более сильной и уверенной.

Рисуем диагональную линию через вершину треугольника. Степень наклона этой линии отвечает за разворот пирамиды.

Соединяем нижние вершины треугольника и диагональ. Таким образом рисуем основание пирамиды и её внешний угол.

Стираем все линии построения, оставляем чистый рисунок.

По-желанию используем цветные материалы и стилизуем пирамиду под камень.

Как нарисовать Египетскую пирамиду через квадрат?

Рассмотрим второй, более академический подход к рисунку пирамиды.

Рисуем искаженный квадрат — основу будущей пирамиды.

Обозначаем точку схода всех лучей. Она должна находится в центре квадрата, выявить эту точку можно с помощью перпендикуляра, который будет проведен с центра основы.

Используем ручку и доводим контуры пирамиды, выполняем стилизацию под камень.

Обозначаем теневые участки. Их положение зависит от того, с какой стороны будет изображено солнце. Не забываем изобразить падающую тень — она добавит реалистичности изображению.

Как нарисовать пейзаж с пирамидами?

Создадим маленький быстрый пейзаж с рядом пирамид.

Легкими штрихами намечаем композицию рисунка. Пирамиды находятся в верхней трети бумаги.

Опираясь на первый пример, рисуем объем пирамид.

Уточняем все контуры и вычищаем изображение от лишних линий.

Штрихуем изображение быстрыми свободными штрихами.

В дальнейшем можно доработать пейзаж цветными материалами и создать быстрый, но очень эффектный скетч.

Источник

Как лучше нарисовать пирамиду

by Колпаков А.Н. on 8 июля 2011

К азалось бы, что может быть сложного или неправильного в изображении пирамиды? Неужели и здесь репетитор по математике не обходится без специальных приемов и методик? Отмечается всего лишь 4 точки (любые 3 из которых не лежат на одной прямой) и соединяются шестью отрезками. И все. Что здесь обсуждать? Но даже в такой простой ситуации репетитору по математике приходится исправлять ученические ошиби. Даже не столько математические, сколько стратегические. Какие? Рисунок, на котором невозможно рассмотреть или показать элементы пространственного тела, подписать значения величин, на котором не развернуться с дополнительными построениями, лучше переделать. Это должен понимать любой репетитор и в начале курса подготовки к ЕГЭ потратить некоторое время на обучение правилам и культуре чертежа. Кроме требований к его аккуратности и удобному расположению информации из условия задачи существуют еще и математические законы его выполнения. Рассмотрим их подробнее.

Правило метода изображений.

Метод изображений — отдельный предмет, изучению которого на математическом факультете МПГУ отводится целый семестр. То, что мы рисуем на бумаге – следы от проекций частей тела на некоторую плоскость. От нее зависит то, какие отрезки и какие сечения будут отчетливо видны, а какие окажутся «наползающими» друг на друга или скрытыми. Когда репетитор по математике решает, с какой стороны нарисовать ученику пирамиду, он определяет расположение плоскости и направление проецирования.

Существуют геометрические законы проецирования простейших стереометрических объектов. Длины непараллельных отрезков, например, при изображении могут менять соотношение своих длин (преподавателю лучше произнести «искажаются»). Если в реальности один из них больше другого, то в проекции может быть все с точностью до наоборот. Тоже самое и с углами. Прямой угол может проецироваться как в острый, так и в тупой. Для того, чтобы репетитору математики убедить в этом ученика стоит покрутить перед его глазами обычный угольник. Однако отношение длин отрезков, лежащих на параллельных или совпадающих прямых, не меняется и, в частности, не искажаются середины сторон многоугольников (граней пирамиды). Это объясняет закон расположения основания высоты правильной треугольной пирамиды: оно должно являться точкой пересечения его медиан (центром тяжести). Не искажается также параллельность. Если в пространстве имеется параллельность между прямыми, то она сохраняется и между их следами. Поэтому изображением основания правильной четырехугольной пирамиды выбирается параллелограмм.

Читабельность рисунка.

Важно расположить пирамиду так, чтобы все ее части не просто были видны, а допускали бы дальнейшее усложнение чертежа: проведение апофем, следов от сечений и т.д.

Для этого строить, например, правильную пирамиду желательно снизу вверх через высоту (так она используется почти во всех задачах). Сначала репетитор по математике рисует основание пирамиды, затем ее центр и из этой точки восстанавливает перпендикуляр. Его верний конец выбирается так, чтобы все наклонные ребра были достаточно удалены друг от друга. Если строить в обратном порядке можно промахнуться с центром многоугольника. Конечно, это не критично для решения задач на правильную треугольную пирамиду, но все равно неприглядно для восприятия. Середины должна отображаться серединами.

Построение основания.
Независимо от вида основания тетраэдра его изображают остроугольным треугольником и вытягивают влево или вправо. Зачем? Если он будет равнобедренным, то одно из боковых ребер закроет высоту (если конечно ее основание правильно расположено). Это показано на рисунке.

Фронтальное изображение тетраэдра. Правило репетитора.

Каким краем лучше всего изобразить пирамиду? То есть как оптимально выбрать плоскость для проецирования? Некоторые преподаватели и репетиторы по математике, к сожалению, не обращают внимание на такую «мелочь» как фронтальное расположение пирамиды. А зря. Существует два вида рисунка: «уголком основания к нам» или «уголком от нас» Рассмотрим рисунок с «уголком ABC от нас»:
Восстанавливаем высоту снизу вверх и выбираем положение ее конца (вершины пирамиды) с расчетом на приемлемый размах грани ABP. Для этого самое главное не попасть точкой P на линию AB. Иначе мы грань не увидим. Значительное отклонение от точки пересечения (в изображении) линий AB и OP вызывает довольно небольшое отклонение луча AP от луча AB и поэтому, чтобы добиться размаха грани ABP, необходимо выбирать точку P или очень низко или очень высоко. Последнее может чрезмерно укрупнить рисунок, вытягивая пирамиду вверх (сокращая пространство для самого решения), а низкая точка делает рисунок мелким. Поэтому я не рекомендую репетиторам по математике работать с таким фронтом. Лучше всего перевернуть треугольник ABC уголком к нам.
Заметьте, что теперь положение точки P никак не сказывается на читабельности грани ABP и если не равнобедренный и «сильно остроугольный», а точка О – его центр тяжести (то есть O не на высоте основания), то высота пирамиды не будет закрыта ребром BP ни при каком расположении вершины P. В этом случае репетитор по математике получает определенную свободу выбора вершины пирамиды, что крайне важно для улучшения читабельности дальнейших построений в сложных задачах.

Прорисовка невидимых линий.
Репетитор по математике, конечно, может обойтись и без пунктиров. Однако что русскому то хорошо, то немцу смерь. Ученику — важно воспринять тело именно с той стороны, с которой его видит репетитор. Особенно при работе с гранями. Я советую преподавателю математики чаще называть грани не по вершинам, а по их естественному расположению: «ближняя», «дальняя», «левая», «правая». Если в голове у ребенка сформируется образ объекта «задом наперед», то возникнут проблемы с описанием хода дополнительных построений, чтением рисунка и даже с объяснением непонятных моментов решений.

о построении четырехугольной пирамиды.
Основание правильной четырехугольной пирамиды следует изображаться в виде параллелограмма. Почему? Конечно, можно так расположить квадрат к плоскости проецирования, чтобы прямые углы сохранились (и мы получим прямоугольник), но тогда апофемы двух ближних граней будут закрывать высоту пирамиды. Другого объяснения сложившимся стандартам изображений я не нахожу.

Александр Колпаков, репетитор по математике в Москве. Подготовка к ЕГЭ.

Сайт вызывает восхищение уровнем профессионализма, прежде всего, в методическом плане. Нашел много поучительного для себя, имея опыт репетиторства с 70-х годов прошлого века (по физике).
Сейчас развивается онлайн репетиторство и там непочатый край работы для мастеров класса Александра Николаевича.

Я,ученик 11 класса,рад что прочитал эту страничку,потому что до этого я рисовал чертежи как попало.Теперь,под конец года, я понял многие вещи о построении фигур.

Источник