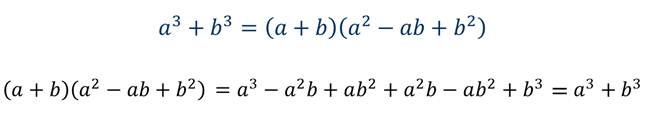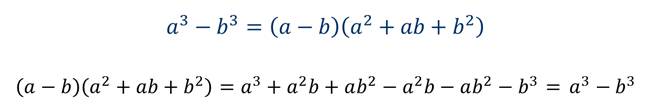Все способы разложения разности кубов

Как использовать куб разности

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула куба разности.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Формула куб разности не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

a 3 − 3a 2 b + 3ab 2 − b 3 = (a − b) 3

Как возвести в куб разность

Рассмотрим пример. Необходимо возвести в куб многочлен, который содержит разность.

Используем формулу куба разности. Только вместо « a » у нас будет « 2y », а вместо « b » будет « x ».

Часто возводят многочлен в куб следующим образом:

Это неверно! Для возведения многочлена в куб необходимо использовать формулу сокращенного умножения: (a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Применение куба разности для разложения многочлена на множители

Рассмотрим многочлен. Требуется разложить его на множители, используя формулу куба разности.

Обратите внимание, что многочлен « x 3 − 3x 2 y + 3xy 2 − y 3 » напоминает правую часть формулы « a 3 − 3a 2 b + 3ab 2 − b 3 », только вместо « a » стоит « x », а на месте « b » стоит « y ».

Используем для многочлена « x 3 − 3x 2 y + 3xy 2 − y 3 » формулу куба разности.

Рассмотрим пример сложнее. Требуется разложить многочлен на множители.

В этом многочлене не так очевидно, что будет являться в формуле « a », а что « b ».

Представим многочлен « 8y 3 − 36y 2 + 54y − 27 » в виде « a 3 − 3a 2 b + 3ab 2 − b 3 ».

Обратим внимание, что « 8y 3 » — это « (2y) 3 », значит « a » в исходном многочлене — это « 2y ».

Чтобы понять, что является « b » в исходном многочлене, рассмотрим последний одночлен — « 27 ». Вспомним, что « 27 » — это « 3 3 », значит « b » в исходном многочлене — это « 3 ».

Рассмотрим одночлены посередине « 36y 2 » и « 54y ». При сравнении многочлена с кубом разности « a 3 − 3a 2 b + 3ab 2 − b 3 » можно понять, что эти одночлены должны быть « 3a 2 b » и « 3ab 2 соответсвенно.

Преобразуем одночлены « 36y 2 » и « 54y » в виде « 3a 2 b » и « 3ab 2 ». С учетом того, что ранее мы нашли, что в нашем многочлене « a » — это « 2y », а « b » — это « 3 ».

Внимательно проверяйте, правильно ли вы разложили числовые коэффициенты.

Проверим, верно ли мы разложили одночлены « 36y 2 » и « 54y ».

• 36y 2 = 3 · (2y) 2 · 3 = 3 · 4y 2 · 3 = 12y 2 · 3 = 36y 2 (верно)
• 54y = 3 · 2y · (3) 2 = 3 · 2y · 9 = 6y · 9 = 54y (верно)

После необходимых преобразований становится видно, что многочлен
« 8y 3 − 36y 2 + 54y − 27 » является правой частью формулы куба разности
« (a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3 ».

Используем формулу куба разности и решим пример до конца.

Источник

Как использовать разность кубов

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2 )

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2 ) = a 3 − b 3

Как разложить на множители разность кубов

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что « 27а 3 » — это « (3а) 3 », значит, для формулы разности кубов вместо « a » мы используем « 3a ».

Используем формулу разности кубов. На месте « a 3 » у нас стоит « 27a 3 », а на месте « b 3 », как и в формуле, стоит « b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов « (x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов « a 3 − b 3 = (a − b)(a 2 + ab + b 2 ) », только вместо « a » стоит « x », а на месте « b » стоит « 1 ».

Используем для « (x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить « (y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
« a 3 − b 3 = (a − b)(a 2 + ab + b 2 ) », то можно понять, что на месте « a » из первой скобки стоит « y 2 , а на месте « b » стоит « 1 ».

Одночлены, которые стоят на месте « a » или « b » могут стоять в степени.

Например, в рассматриваемом примере на месте « a » стоит « y 2 ». Это означает, что именно « y 2 » мы рассматриваем как « a ».

Представим скобку « (y 4 + y 2 + 1) » таким образом, чтобы она соответствовала правой части формулы разности кубов.

Используем формулу разности кубов и решим пример до конца.

Источник

Разложение на множители суммы и разности кубов

Урок 36. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Разложение на множители суммы и разности кубов»

· показать, что формулы куба суммы и куба разности можно применять для разложения многочленов на множители.

Для разложения на множители суммы кубов используется одна из формул сокращённого умножения, которая называется формулой суммы кубов.

Обратите внимание, что один из множителей в правой части формулы:

Читают формулу суммы кубов так: сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Для разложения на множители разности кубов используется следующая формула сокращённого умножения, которая называется формулой разности кубов.

Читают формулу разности кубов следующим образом: разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Таким образом, к уже известным нам способам разложения многочленов на множители, а это: вынесение общего множителя за скобки, способ группировки, разложение на множители с помощью формул квадрата суммы и квадрата разности, с помощью формулы разности квадратов, а также с помощью формул куба суммы и куба разности; мы можем добавить способ разложения на множители с помощью формул суммы и разности кубов.

Рассмотрим несколько примеров применения новых формул.

Источник

Сокращенное умножение: правила, формулы

О чем эта статья:

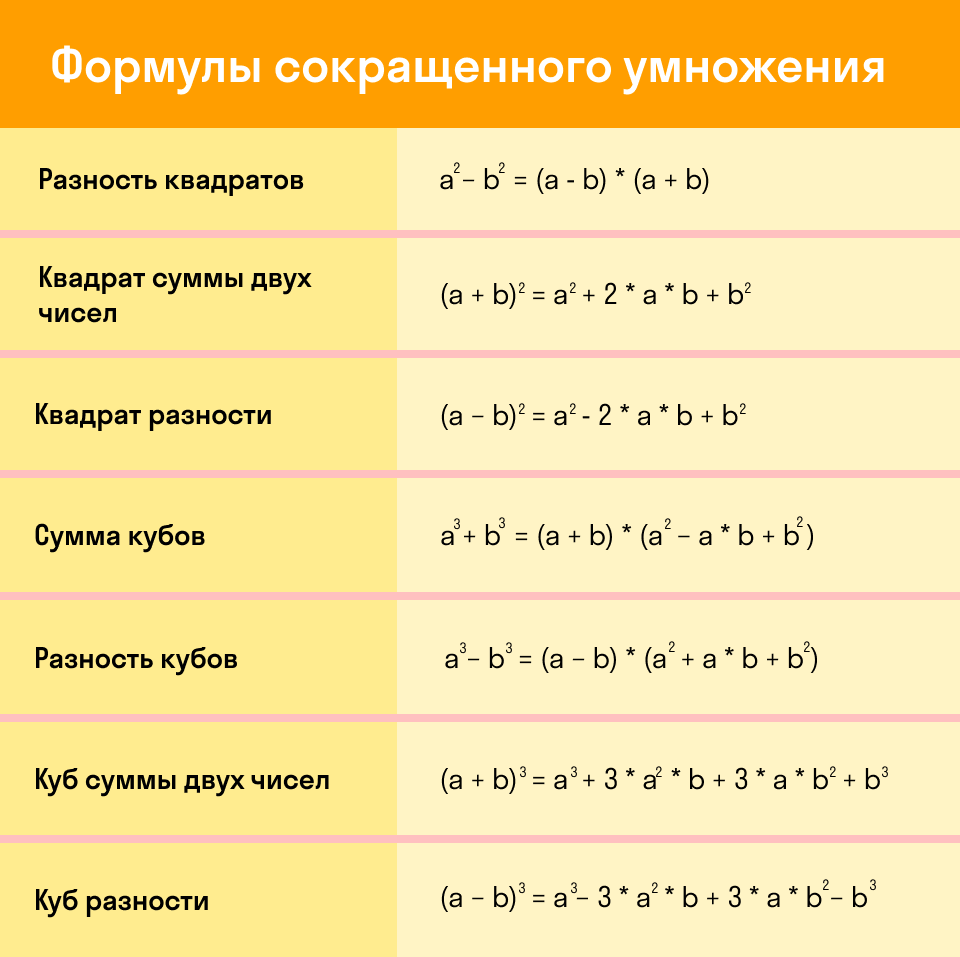
Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

1. Разность квадратов двух выражений равна произведению их разности и их суммы.
2. Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
3. Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
4. Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
5. Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
6. Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
7. Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .

Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .

Докажем, что a 2 — b 2 = (a — b) * (a + b).

Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

a 2 — b 2 = a 2 — b 2 + ab — ab

1. Сгруппируем иначе: a 2 — b 2 + a * b — a * b = a 2 — a * b + a * b — b 2
2. Продолжим группировать: a 2 — a * b — b 2 +a * b = (a 2 — a * b) + (a * b — b 2 )
3. Вынесем общие множители за скобки:

   (a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)

1. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
2. Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
3. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Что сделать: вычислить квадрат произведения (55 + 10) 2 .

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).

Как решаем:

1. Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
2. Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник