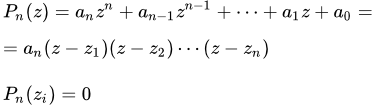Все способы разложения многочлена

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник

Методы разложения многочленов на множители

Основа метода

Пусть

– многочлен степени n ≥ 1 от действительной или комплексной переменной z с действительными или комплексными коэффициентами a_i . Примем без доказательства следующую теорему.

Теорема 1

Уравнение P_n ( z ) = 0 имеет хотя бы один корень.

Докажем следующую лемму.

Лемма 1

Пусть P_n ( z ) – многочлен степени n , z ₁ – корень уравнения:
P_n ( z ₁) = 0 .
Тогда P_n ( z ) можно представить единственным способом в виде:
P_n ( z ) = ( z – z ₁) P_{n– 1} ( z ) ,
где P_{n– 1} ( z ) – многочлен степени n – 1 .

Доказательство

Для доказательства, применим теорему (см. Деление и умножение многочлена на многочлен уголком и столбиком), согласно которой для любых двух многочленов P_n ( z ) и Q_k ( z ) , степеней n и k , причем n ≥ k , существует единственное представление в виде:
P_n ( z ) = P_n–k ( z ) Q_k ( z ) + U_{k– 1} ( z ) ,
где P_n–k ( z ) – многочлен степени n–k , U_{k– 1} ( z ) – многочлен степени не выше k– 1 .

Положим k = 1 , Q_k ( z ) = z – z ₁ , тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) + c ,
где c – постоянная. Подставим сюда z = z ₁ и учтем, что P_n ( z ₁) = 0 :
P_n ( z ₁ ) = ( z ₁ – z ₁ ) P_{n– 1} ( z ₁ ) + c ;
0 = 0 + c .
Отсюда c = 0 . Тогда
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) ,
что и требовалось доказать.

Разложение многочлена на множители

Итак, на основании теоремы 1, многочлен P_n ( z ) имеет хотя бы один корень. Обозначим его как z ₁ , P_n ( z ₁ ) = 0 . Тогда на основании леммы 1:
P_n ( z ) = ( z – z ₁ ) P_{n– 1} ( z ) .
Далее, если n > 1 , то многочлен P_{n– 1} ( z ) также имеет хотя бы один корень, который обозначим как z ₂ , P_{n– 1} ( z ₂ ) = 0 . Тогда
P_{n– 1} ( z ) = ( z – z ₂ ) P_{n– 2} ( z ) ;
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) P_{n– 2} ( z ) .

Продолжая этот процесс, мы приходим к выводу, что существует n чисел z ₁ , z ₂ , . , z _n таких, что
P_n ( z ) = ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) P ₀ ( z ) .
Но P ₀( z ) – это постоянная. Приравнивая коэффициенты при z n , находим что она равна a_n . В результате получаем формулу разложения многочлена на множители:
(1) P_n ( z ) = a_n ( z – z ₁ )( z – z ₂ ) . ( z – z _n ) .

Числа z_i являются корнями многочлена P_n ( z ) .

В общем случае не все z_i , входящие в (1), различны. Среди них могут оказаться одинаковые значения. Тогда разложение многочлена на множители (1) можно записать в виде:
(2) P_n ( z ) = a_n ( z – z ₁ ) n ₁ ( z – z ₂ ) n ₂ . ( z – z _k ) n_k ;
.
Здесь z_i ≠ z_j при i ≠ j . Если n_i = 1 , то корень z_i называется простым. Он входит в разложение на множители в виде ( z–z_i ) . Если n_i > 1 , то корень z_i называется кратным корнем кратности n_i . Он входит в разложение на множители в виде произведения n_i простых множителей: ( z–z_i )( z–z_i ) . ( z–z_i ) = ( z–z_i ) n_i .

Многочлены с действительными коэффициентами

Далее мы считаем, что многочлен

имеет действительные коэффициенты a_i .

Лемма 2

Если – комплексный корень многочлена с действительными коэффициентами, , то комплексно сопряженное число также является корнем многочлена, .

Доказательство

Действительно, если , и коэффициенты многочлена – действительные числа, то .

Таким образом, комплексные корни входят в разложение на множителями парами со своими комплексно сопряженными значениями:
,
где , – действительные числа.
Тогда разложение (2) многочлена с действительными коэффициентами на множители можно представить в виде, в котором присутствуют только действительные постоянные:
(3) ;
.

Методы разложения многочлена на множители

С учетом сказанного выше, для разложения многочлена на множители, нужно найти все корни уравнения P_n(z) = 0 и определить их кратность. Множители с комплексными корнями нужно сгруппировать с комплексно сопряженными. Тогда разложение определяется по формуле (3).

Таким образом, метод разложения многочлена на множители заключается в следующем:
1. Находим корень z ₁ уравнения P_n ( z ₁) = 0 .
2.1. Если корень z ₁ действительный, то в разложение добавляем множитель ( z – z ₁) и делим многочлен P_n(z) на ( z – z ₁) . В результате получаем многочлен степени n – 1 :
.
Далее повторяем процесс для многочлена P_{n– 1} (z) , начиная с пункта 1, пока не найдем все корни.
2.2. Если корень комплексный, то и комплексно сопряженное число является корнем многочлена. Тогда в разложение входит множитель

,
где b ₁ = – 2 x ₁ , c ₁ = x ₁ 2 + y ₁ 2 .
В этом случае, в разложение добавляем множитель ( z 2 + b ₁ z + c ₁) и делим многочлен P_n(z) на ( z 2 + b ₁ z + c ₁) . В результате получаем многочлен степени n – 2 :
.
Далее повторяем процесс для многочлена P_{n– 2} (z) , начиная с пункта 1, пока не найдем все корни.

Нахождение корней многочлена

Главной задачей, при разложении многочлена на множители, является нахождение его корней. К сожалению, не всегда это можно сделать аналитически. Здесь мы разберем несколько случаев, когда можно найти корни многочлена аналитически.

Корни многочлена первой степени

Многочлен первой степени – это линейная функция. Она имеет один корень. Разложение имеет только один множитель, содержащий переменную z :
.

Корни многочлена второй степени

Чтобы найти корни многочлена второй степени, нужно решить квадратное уравнение:
P ₂( z ) = a ₂ z 2 + a ₁ z + a ₀ = 0 .
Если дискриминант 0″ style=»width:167px;height:22px;vertical-align:-12px;background-position:-392px -473px»> , то уравнение имеет два действительных корня:
, .
Тогда разложение на множители имеет вид:
.
Если дискриминант D = 0 , то уравнение имеет один двукратный корень:
;
.
Если дискриминант D 0 , то корни уравнения комплексные,
.

Многочлены степени выше второй

Существуют формулы для нахождения корней многочленов 3-ей и 4-ой степеней. Однако ими редко пользуются, поскольку они громоздкие. Формул для нахождения корней многочленов степени выше 4-ой нет. Несмотря на это, в некоторых случаях, удается разложить многочлен на множители.

Нахождение целых корней

Если известно, что многочлен, у которого коэффициенты – целые числа, имеет целый корень, то его можно найти, перебрав все возможные значения.

Лемма 3

Пусть многочлен
,
коэффициенты a_i которого – целые числа, имеет целый корень z ₁ . Тогда этот корень является делителем числа a ₀ .

Доказательство

Перепишем уравнение P_n ( z ₁) = 0 в виде:
.
Тогда – целое,
M z ₁ = – a ₀ .
Разделим на z ₁ :
.
Поскольку M – целое, то и – целое. Что и требовалось доказать.

Поэтому, если коэффициенты многочлена – целые числа, то можно попытаться найти целые корни. Для этого нужно найти все делители свободного члена a ₀ и, подстановкой в уравнение P_n ( z ) = 0 , проверить, являются ли они корнями этого уравнения.
Примечание. Если коэффициенты многочлена – рациональные числа, , то умножая уравнение P_n ( z ) = 0 на общий знаменатель чисел a_i , получим уравнение для многочлена с целыми коэффициентами.

Нахождение рациональных корней

Если коэффициенты многочлена – целые числа и целых корней нет, то при a_n ≠ 1 , можно попытаться найти рациональные корни. Для этого нужно сделать подстановку
z = y/a_n
и умножить уравнение на a_n n- 1 . В результате мы получим уравнение для многочлена от переменной y с целыми коэффициентами.Далее ищем целые корни этого многочлена среди делителей свободного члена. Если мы нашли такой корень y_i , то перейдя к переменной x , получаем рациональный корень
z_i = y_i /a_n .

Полезные формулы

Приведем формулы, с помощью которых можно разложить многочлен на множители.

В более общем случае, чтобы разложить многочлен
P_n ( z ) = z n – a ₀ ,
где a ₀ – комплексное, нужно найти все его корни, то есть решить уравнение:
z n = a ₀ .
Это уравнение легко решается, если выразить a ₀ через модуль r и аргумент φ :
.
Поскольку a ₀ не изменится, если к аргументу прибавить 2 π , то представим a ₀ в виде:
,
где k – целое. Тогда
;
.
Присваивая k значения k = 0, 1, 2, . n– 1 , получаем n корней многочлена. Тогда его разложение на множители имеет вид:
.

Биквадратный многочлен

Рассмотрим биквадратный многочлен:
.
Биквадратный многочлен можно разложить на множители, без нахождения корней.

Далее раскладываем квадратные многочлены на множители, если соответствующие многочлены имеют действительные корни.

Бикубический и многочлены, приводящиеся к квадратному

Рассмотрим многочлен:
.
Его корни определяются из уравнения:
.
Оно приводится к квадратному уравнению подстановкой t = z n :
a _{2 n} t 2 + a_n t + a ₀ = 0 .
Решив это уравнение, найдем его корни, t ₁ , t ₂ . После чего находим разложение в виде:
.
Далее методом, указанным выше, раскладываем на множители z n – t ₁ и z n – t ₂ . В заключении группируем множители, содержащие комплексно сопряженные корни.

Возвратные многочлены

Многочлен называется возвратным, если его коэффициенты симметричны:

Пример возвратного многочлена:
.

Если степень возвратного многочлена n – нечетна, то такой многочлен имеет корень z = –1 . Разделив такой многочлен на z + 1 , получим возвратный многочлен степени n – 1 .
Если степень возвратного многочлена n – четна, то подстановкой , он приводится к многочлену степени n/ 2 . См. Пример с возвратным многочленом >>>.

Автор: Олег Одинцов . Опубликовано: 11-06-2015 Изменено: 30-04-2016

Источник