8 ферзей на шахматной доске
Восемь ферзей на шахматной доске — головоломка, которая адресована начинающим игрокам для развития пространственного мышления и аналитических способностей. Автором задачи стал теоретик шахмат Макс Беззель (1824-1871). Условия головоломки были сформулированы в 1848 году: игроку предстояло расположить на классической шахматной доске восемь ферзей так, чтобы ни одна из фигур не находилась под боем любой другой. Задача усложняется геометрией ферзевых ходов, которые осуществляются не только по вертикали или горизонтали, но и в диагональном направлении.
Классическая версия головоломки может формулироваться в нескольких вариантах:
- найти любое допустимое решение;
- выявить все возможные варианты решений;
- доказать возможность решения задачи.
Модифицированная версия головоломки Беззеля используется при обучении школьников основам программирования и математического анализа. Ученикам предлагается расставить N фигур на доске N×N клеток. В качестве N выступает любое целое число. Многочисленные исследования показали, что при значениях переменной, равным 2, 3 или 4, задача становится нерешаемой.
Допустимые варианты решения
За 170 лет шахматистам удалось найти 12 базовых решений для головоломки Беззеля. Они рассматриваются в качестве основных во всех учебниках по шахматной теории. Учет правил симметрии позволит расширить число доступных решений до 92: расположение фигур относительно друг друга будет неизменным, варьируются только координаты клеток с ферзями.
Карл Гаусс, известный математик и любитель шахмат, смог выявить 72 варианта расстановки. Ученый использовал своеобразный подход: при обнаружении подходящего решения он последовательно разворачивал доску вокруг оси с шагом в девяносто градусов. Так появлялись «дополнительные» варианты расстановки без длительных изысканий.
Как расставить 8 ферзей на доске
Головоломка Беззеля рассматривается тренерами как задача средней сложности: подходящее решение могут обнаружить новички за несколько минут. Наиболее известная расстановка фигур отражена в таблице.
| Номер ферзя | Координаты |
| Первый | h5 |
| Второй | f1 |
| Третий | d8 |
| Четвертый | b4 |
| Пятый | g7 |
| Шестой | e3 |
| Седьмой | c6 |
| Восьмой | a2 |
Три дополнительных варианта можно получить с помощью последовательного поворота доски по предложенному Гауссом принципу. Аналогичным образом действует зеркальное отражение расстановки фигур.
Решение задачи о восьми ферзях полезно для формирования навыков счета ходов, анализа текущей позиции на доске и поиска быстрого ответа на комбинацию соперника. Новичкам рекомендуется искать варианты расстановки фигур без использования ухищрений в виде поворотов игрового поля. В этом случае все обнаруженные решения станут результатом интеллектуальных усилий игрока.
Модифицированные условия задачи Беззеля часто используются в математических секциях или на уроках информатики. Так, осваивающие основы программирования ученики могут создать скрипт для поиска решений при фиксированном или произвольном значении переменной N, обозначающей количество расставляемых на доске фигур и размеры игрового поля.
Источник
Все способы расстановки ферзей





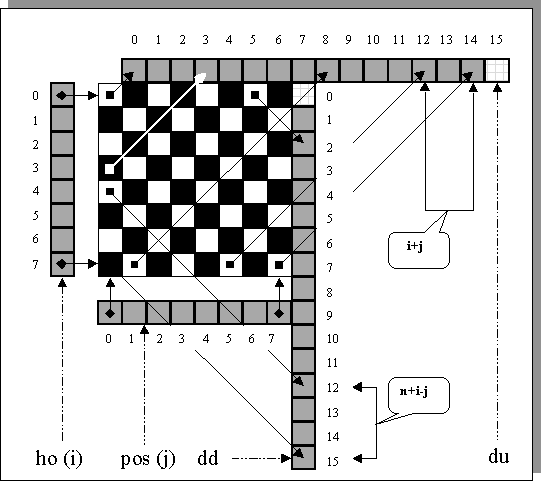
Простой и наглядный алгоритм перебора с возвратом реализуется в следующей хорошо известной задаче Гаусса о расстановке ферзей на шахматной доске. Нам удобно формулировать (и решать) эту задачу сразу для доски размером n ´ n (n =1, 2, …). Будем считать, что её строки и столбцы пронумерованы соответственно сверху вниз и слева направо цифрами от 0 до n— 1 (см. рис.1 при n=8).
Решение. В соответствии с описанной ранее общей схемой 2 алгоритма перебора с возвратом предложенную задачу можно было бы решать по приведенному ниже алгоритму “Все расстановки”. По нему ферзи расставляются последовательно на вертикалях с номерами от нуля и далее. В процессе выполнения предписания возможны снятия ферзей с доски (возвраты).
Рис. 1. Схема использования вспомогательных массивов в задаче 1
Алгоритм “Все расстановки”
Полагаем D = Æ , j = 0 (D — множество решений, j — текущий столбец для очередного ферзя).
Пытаемся в столбце j продвинуть вниз по вертикали или новый (если столбец j пустой), или уже имеющийся там ферзь на ближайшую допустимую строку. Если это сделать не удалось, то переходим к пункту 4.
j ¬ j +1. Если j 1, то переходим к пункту 2. В противном случае j = n— 1, то есть все вертикали уже заняты. Найденное частичное решение запоминаем в множестве D и переходим к пункту 2.
j ¬ j-1 , то есть снимаем ферзь со столбца j и переходим к предыдущему столбцу. Если j ³ 0, то выполняем пункт 2. Иначе вычисления прекращаем. Решения задачи находятся в множестве D , которое, вообще говоря, может быть и пустым.
Никто и ничто не мешает нам при небольших n пытаться выполнить этот алгоритм “вручную”. Но чтобы идти дальше и пытаться переложить эти заботы на компьютер, необходимо остановиться на каком-либо представлении для данных.
Введем в рассмотрение четыре вспомогательных вектора: pos, ho, dd и du c длинами n, n, 2 × n— 1 и 2 × n— 1 соответственно. Использовать их будем следующим образом (см. рис.1):
 |
 |
 |
 |
Использование этих соглашений позволяет получить такие утверждения:
 |
 |
 |
С учетом сказанного достаточно компактный рекурсивный вариант алгоритма решения задачи 1 можно было бы задать следующими двумя функциями:
Дадим краткое описание функций queen () и qu().
Головная функция queen(n ) организует обращение к рекурсивной функции qu (), передавая ей в качестве фактических параметров:
 |
 |
 |
 |
Возвращает функция queen () матрицу ot , столбцы которой, кроме нулевого, содержат решения задачи. Если (i0, i1, . in-1) T — один из таких столбцов, то решением являются позиции ферзей: (i0, 0), (i1, 1), . (in-1, n-1) .
Функция qu () в рекурсивном варианте реализует алгоритм “Все расстановки”. Нелишне отметить, что рекурсия здесь осуществляется по не совсем стандартной схеме. В каждом рекурсивном вызове глубины j делается попытка поместить ферзь в некоторую позицию i столбца j (i, j = 0, 1, …, n— 1), а сам вызов соответствует переходу от работы с текущим столбцом к работе со следующим столбцом. При этом в начале вычислений и при переходах к любому последующему рекурсивному вызову параметр i меняется от нуля и далее с шагом, равным единице, пытаясь принять значение наименьшего номера поля, допустимого для установки ферзя. При переходах к любому предыдущему рекурсивному вызову параметр i продолжает изменяться от своего текущего на данном уровне значения с шагом, равным единице, также пытаясь принять значение наименьшего номера поля, допустимого для установки ферзя. Если в текущем столбце ферзь установить уже не удается, то создавшуюся ситуацию (позицию) назовем тупиком. Попадание в тупик приводит к завершению текущего рекурсивного вызова, то есть к возврату к предыдущему столбцу и продолжению работы с ним. Иных случаев завершения рекурсивных вызовов не существует. Поэтому базой рекурсии мы должны считать совокупность всех тупиков. Заметим, что в данном случае элементы базы заранее до вычислений неизвестны.
После установки ферзя в одну из строк i последнего столбца j = n— 1 формируется одно из решений задачи. Вычисления прекращаются, когда мы попадаем в тупик при работе со столбцом 0. Полученные решения задачи, если они есть, возвращаются в виде столбцов матрицы ot , начиная от первого и далее.
Попробуем теперь понять, как реализуется декомпозиция. Для этого вместо исходной задачи удобно решать её следующее обобщение.
Задача E(n, m, w ). На доске размера n ´ m (m = n, n— 1,…0) требуется установить m ферзей так, чтобы они не били друг друга. При этом имеются некоторые клетки доски, на которые ферзь заведомо ставить нельзя. Множество этих “запретных” клеток обозначим через w .
Исходная задача есть E(n, n, Æ ). Проведем её декомпозицию. Представим доску в виде двух частей: нулевого столбца ( A ) и оставшейся части ( B ). Соответственно этому разбиению будем решать задачи E(n, 1, Æ ) и E(n, n-1, w ). Каждое из n возможных решений i (ферзь установлен в строке i = 0, 1, …, n— 1) первой задачи однозначно определяет множество w = w (i ) запретных клеток для второй задачи. При этом в w (i ) попадают те клетки B , которые в “объединенной” доске бьет ферзь, установленный в строке i доски A . Пусть i зафиксировано и найдено множество d(i ) решений второй задачи E(n, n-1, w (i )) для доски B . Тогда расположение ферзя в строке i доски A и любое из полученных решений x Î d(i ) на B в совокупности дают различные решения ot(i ) исходной задачи E(n, n, Æ ). Для получения всех решений этой задачи остается лишь взять объединение по i множеств ot(i): ot = È ot(i).
x T = [0 4 7 5 2 6 1 3], y T = [1 6 4 7 0 3 5 2];
2. c := queen(3), cols(c) = 1, то есть решений нет!
Замечание. В функции qu () можно вообще отказаться от использования цикла, организовав рекурсию как по i , так и по j . В этом случае qu () и queen () могли бы выглядеть так:
Обратите внимание на то, как реализована в qu () рекурсия. Во-первых, её глубина равна n 2 — при каждом рекурсивном вызове по j (j = 0, 1, …, n— 1) происходит n рекурсивных вызовов по i (i = 0, 1, …, n— 1). Поскольку при каждом рекурсивном вызове с фиксированными значениями i и j осуществляется попытка установить ферзь на поле ( i, j ), то и сами вызовы здесь удобно не нумеровать от 0 до n 2 -1, а обозначать упорядоченными парами индексов ( i, j).
Другой вариант для функции qu () получится, если поменять местами порядок рекурсивных обращений по i и по j . В этом случае отпадает надобность в снятии меток (предпоследняя строка qu ()). Функция queen () при этом останется прежней. Но решения будут возвращаться в порядке, обратном тому, который был раньше:
Впрочем, для возвращения решений по этому варианту qu () в прежнем порядке достаточно при проведении рекурсии по параметру i менять его не от 0 до n— 1, а от n— 1 до 0. При этом при обращениях к qu () на месте параметра i в программы необходимо внести такие изменения (в тексте они выделены):
Решение. Предложенную задачу можно решать по приведенным в задаче 1 функциям, упростив их следующим образом. Вместо запоминания найденных решений будем подсчитывать в переменной ot их количество. В этом случае становится ненужным и вспомогательный вектор pos для формирования очередного решения. Эта модификация функций qu () и queen () приводит нас соответственно к функциям qun () и queennum():
Рекурсия в qun () организована точно так же, как и в функции qu().
Просчеты по программе queennum(n ) при разных значениях n приводят к следующим результатам:
Источник