Определение действительной /натуральной/ величины углов
Определение угла между прямыми. Определение угла между прямой и плоскостью. Определение угла между плоскостями.
При определении действительной величины углов должны быть рассмотрены следующие три задачи.
1. Определение угла между двумя пересекающимися прямыми.
2. Определение угла между прямой и плоскостью
3. Определение угла между двумя плоскостями
9.1 Определение натуральной величины угла между двумя пересекающимися прямыми
Для того, чтобы угол между прямыми проецировался в натуральную величину необходимо, чтобы обе стороны этого угла были параллельны данной плоскости проекций, т.е.чтобы плоскость угла была плоскостью уровня.
При решении этой задачи наиболее рациональным, а поэтому, наиболее распространенным путем решения, является преобразование чертежа способом вращения плоскости вокруг одной из ее прямых уровня /см. лекции №6/. При этом способе плоскость общего положения сразу преобразуется в плоскость уровня.
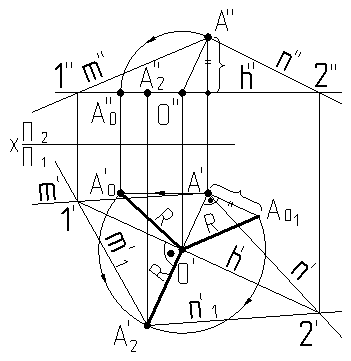
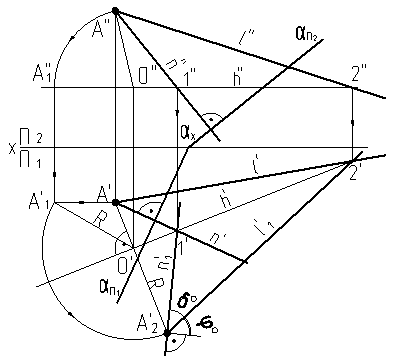
Определить истинное значение угла между пересекающимися прямыми m и n/рис.9.1/.
В плоскости угла строим произвольную горизонталь h(h¢, h¢¢), которая принадлежит плоскостиh Î a (nÇ m) по I признаку принадлежности/1,2/. Вращая плоскость a (nÇ m)вокруг горизонтали hдо положения параллельного плоскости p1, находим натуральную величину плоскости a (nÇ m), и, следовательно, натуральную величину искомого угла при вершине K – угол j°. При решении находим центр вращения Oточки Kи натуральную величину радиуса вращения Rточки Kдвумя способами. Один способ – способ вращения, другой – метод прямоугольного треугольника.
9.2 Определение натуральной величины угла между прямой и плоскостью
Угол между прямой и плоскостью можно определить двумя разными путями.
1.Путем определения непосредственно самого угла.
2.Путем определения дополнительного угла.
Путь определения непосредственно самого угла. При решении первой задачи отыщем непосредственно угол j°— угол между прямой и плоскостью.
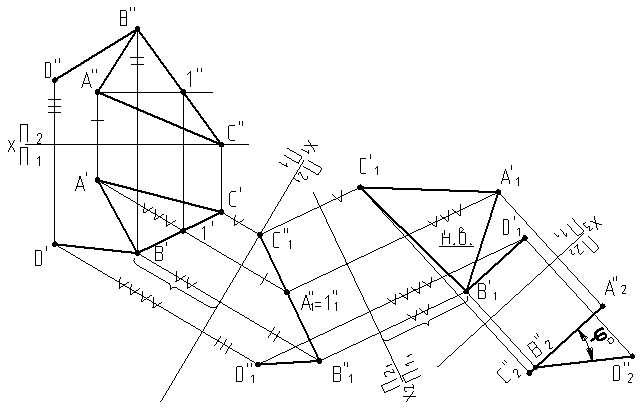
Задача 1. Определить угол между прямой BDи плоскостью треугольника ôABC/рис. 9.2/.
Угол j°между прямой BD и плоскостью ôABCпроецируется в натуральную величину на одну из плоскостей проекций в том случае, если заданная плоскость будет по отношению к этой плоскости проекций проецирующей, а прямая – прямой уровня, т.е. будет параллельной этой плоскости проекций.
Преобразуя чертеж с целью достижения такого расположения плоскости и прямой, следует следить за тем, чтобы в результате такого преобразования не произошло относительного перемещения прямой и плоскости, при котором искомый угол j°изменит свою величину.
На рис.9.2а, рис.9.2б, рис.9.3в даны разные приемы преобразования чертежа для определения непосредственно самого угла j°.
Вводим новую плоскость проекций p21, по отношению к которой плоскость треугольника ôABCбудет проецирующей. Однако, угол между прямой BDи плоскостью треугольника не будет проецироваться на p21 в натуральную величину, т.к. прямая BDне будет параллельна плоскости p21. Введем еще новую плоскость проекций p11, параллельную плоскости треугольника ôABC.В системе плоскостей проекций p21/p11 плоскость треугольника стала горизонтальной плоскостью. Введем еще одну плоскость проекций p22 параллельную прямой B¢1D¢1, учитывая, что предыдущее положение плоскости ôABCбыло проецирующим, то и последующее положение этой плоскости после замены плоскостей проекций также будет проецирующим. Следовательно, после третьей замены плоскостей проекций, мы получим плоскость ôABCв проецирующем положении, а прямую BDв положении линии уровня. Мы получили сам угол j°между прямой BDи плоскостью треугольника ôABC, используя только способ перемены плоскостей проекций./рис.9.2а/.
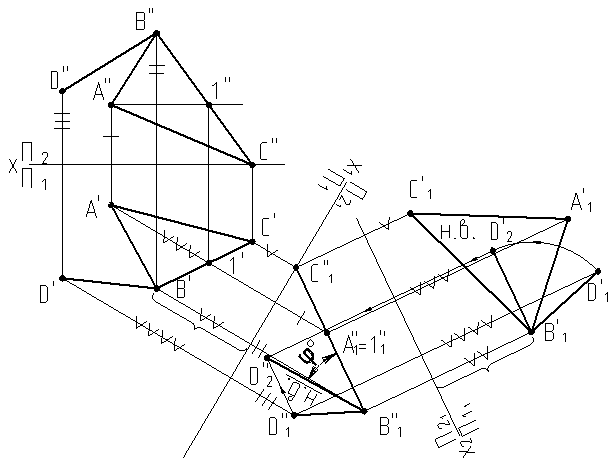
На рис.9.2б используем комбинированный прием. Мы можем повернуть прямую BDвокруг оси, перпендикулярной к p11 до положения, при котором она станет параллельной плоскости p21 . Поскольку ось вращения, перпендикулярная к p11 , будет, одновременно, перпендикулярна к плоскости треугольника, то при таком вращении прямой BD, ее угол наклона к плоскости треугольника не будет менять свою величину. Повернув прямую BDдо положения, параллельное p21 , мы добились того, что угол j° между прямой BDи плоскостью треугольника ôABCпроецируется на эту плоскость проекций в натуральную величину.
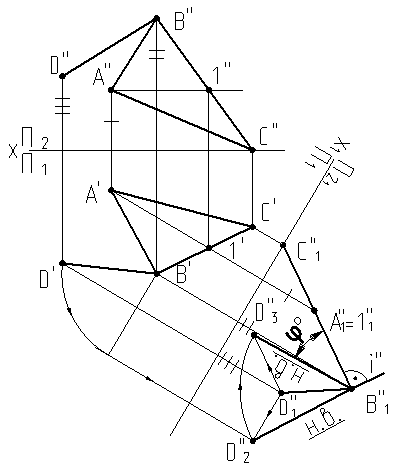
На рис.9.2в используем комбинированный прием, так называемого двойного вращения. В плоскости p21 выбираем ось вращения i¢¢перпендикулярную к плоскости ôABC, которая находится в проецирующем положении. Находим траекторию вращения конца отрезкаBD точки D – это плоскость параллельна плоскости треугольника ôABC, а отрезок будет описывать коническую поверхность, очерковая образующая которой будет натуральной величиной отрезка BD.Находим эту величину отрезка путем вращения вокруг другой оси, перпендикулярной к плоскости проекций p1 в точке B.Находим натуральную величину отрезка BD в плоскости проекций p21. Находим очерковую образующую конической поверхности, а, следовательно, и угол j°.
К решению задачи на определение угла между прямой и плоскостью можно подойти с иных позиций.
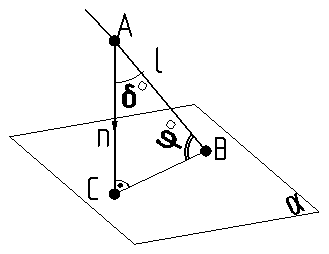 Рис.9.3 | На рис.9.3 мы видим, что если прямая lобразует с плоскостью aугол j°,то та же прямая lс перпендикуляром к этой плоскости – прямой nобразует угол d°. Поскольку треугольник ôABCпрямоугольный, то сумма углов j°+d°=90°равна прямому углу, т.е. 90°. Видим, что угол d°дополняет угол j°до 90°. |
Эта простая зависимость позволяет нам, в некоторых задачах на отыскание угла между прямой и плоскостью, отыскивать не сам угол j°, а дополнительный угол d°. Рассмотрим такую задачу/рис.9.4/.
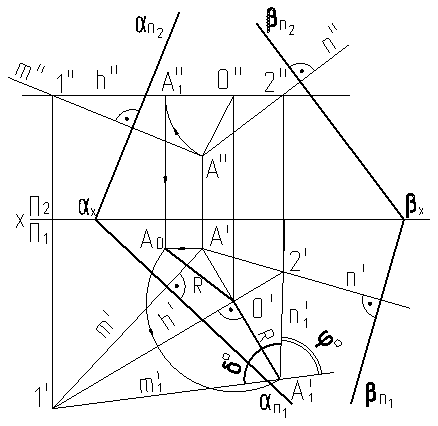
Задача 2. Определить натуральную величину угла между прямой lи плоскостью a (ap1, ap2), заданной следами./рис.9.4/.
Взяв на прямой lпроизвольную точкуA, опускаем из этой точки перпендикуляр на плоскость a— прямую n. Угол между прямыми l и n, и будет искомым углом d°. Проводим в плоскости этого угла произвольную горизонталь h. Находим горизонталь h на p1, используя I признак принадлежности точки 1-2. Затем, вращая вершину A вокруг горизонтали h¢, находим центр O вращения точкиAи натуральную величину радиуса вращенияRвершиныA. Если в плоскости найдется хотя бы одна прямая линией уровня, то и плоскость будет в натуральную величину. Соединяем вершину A¢2 с точками 1¢ и 2¢ получаем плоскость уровня, в которой в натуральную величину будет угол d°. Угол, дополняющий угол d° до 90, и будет j°, который нам требуется определить по условию задачи.
Последний путь решения можно применить не только в тех случаях, когда плоскость задана следами. В общем случае, в плоскости, как бы она не была задана, всегда можно провести горизонталь и фронталь . Наличие этих прямых позволит нам легко провести перпендикуляр к этой плоскости, а затем, как в настоящем примере, определить угол d°, а затем, и угол j°.
9.3 Определение натуральной величины угла между двумя плоскостями
Эта задача, как и предыдущая, может быть решена двумя путями.
1.Путем определения непосредственно самого угла.
2.Путем определения дополнительного угла.
Вначале рассмотрим первый путь решения.
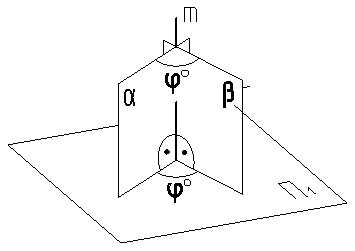 Рис.9.5 | На рис.9.5 изображен двугранный угол между плоскостями aиb. Он будет проецироваться на одну из плоскостей проекций, в нашем примере на p1, в натуральную величину в том случае, если линия пересечения этих плоскостей – прямая m будет перпендикулярна к этой плоскости проекций p1. |
В том случае, если, по условиям задачи, прямая mокажется прямой общего положения, то чертеж следует преобразовать так, чтобы прямая mстала проецирующей /вторая основная задача на преобразование чертежа/.
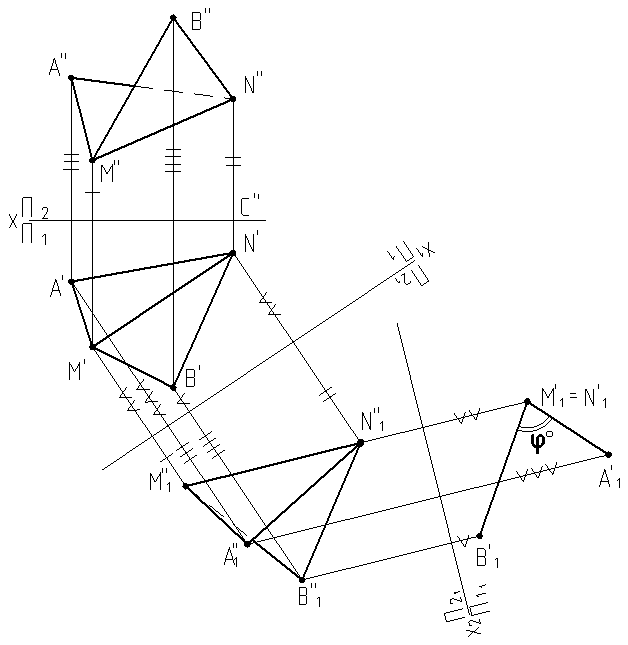
Определить натуральную величину угла j°между треугольниками ôAMNи ôBMN /рис.9.6/.
В данной задаче нет необходимости отыскивать линию пересечения плоскостей, т.к. такая линия на чертеже уже есть – ею является общая сторона треугольников – прямая M N(M¢N¢, M¢¢N¢¢). Преобразуем чертеж способом замены плоскостей проекций. В новой системе плоскостей проекций p21/p11 прямая M Nстановится горизонтально – проецирующей прямой, а плоскости треугольников ôAMN, ôBMN– горизонтально – проецирующими плоскостями. Угол j°, который мы видим на плоскости p11 , является мерой натуральной величины двугранного угла между заданными треугольниками.
Теперь рассмотрим второй путь решения задачи, при котором отыскивается не угол j° — угол между плоскостями, а угол d°— угол между перпендикулярами к этим плоскостям. Такой путь решения в некоторых случаях является более рациональным.
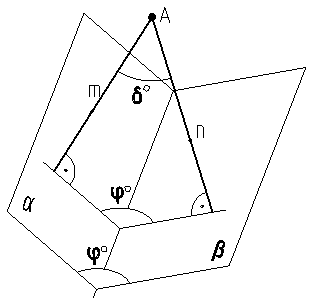 Рис.9.7 | Из рис.9.7 мы видим, что угол изображен двугранный угол d° между перпендикулярами m и n, проведенными к плоскостям aиb через произвольную точку A, в сумме с искомым углом j°составляет180°. Т.е. можно сказать, что угол d°дополняет угол j°до180°. Отсюда становится очевидным, что, зная угол d°, мы всегда сумеем легко определить и угол j°. |
Рассмотрим этот путь решения на примере следующей задачи.
Определить натуральную величину угла между плоскостями aиb/рис. 9.8/.
Из произвольно выбранной точки Aпроводим перпендикуляры к заданным плоскостям: m – к плоскости a, n– к плоскости b. В плоскости, заданной перпендикулярами, проводим произвольную горизонталь h, используя 1признак принадлежности /точки 1,2/, находим горизонталь на p1. Путем вращения вокруг этой горизонтали определяем натуральную величину плоскости, заданной пересекающимися прямыми nÇ m . Определяем натуральную величину d°. Дополняя этот угол до 180°, находим натуральную величину искомого угла j°.
Содержание лекции №9 изложено в учебнике С.А.Фролова /изд. 1978/ на стр. 162-163, 168-172.
| | | следующая лекция ==> |
| Физико-химические изменения крахмала: ретроградация, деструкция, модификация | | |
Дата добавления: 2015-11-18 ; просмотров: 4195 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ УГЛА
Используя свойства ортогональной проекции прямого угла, можно решать задачи на определение натуральной величины угла между:
· 
двумя скрещивающимися прямыми;
· двумя пересекающимися прямыми;
· угла наклона прямой к плоскости;
· угла между двумя пересекающимися плоскостями.
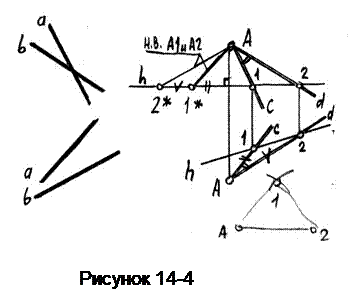
Пример 12. Определить натуру угла между скрещивающимися прямыми aиb(рисунок 14-4).
Через произвольную точку А проведем прямые си d, параллельные прямым а и b. В полученной плоскости проведем горизонталь и построим натуральную величину Δ А-1-2 (способом засечек, предварительно определив натуру каждой его стороны).
Угол при вершине А будет искомым.
Пример 13. Определить угол наклона прямой n к плоскости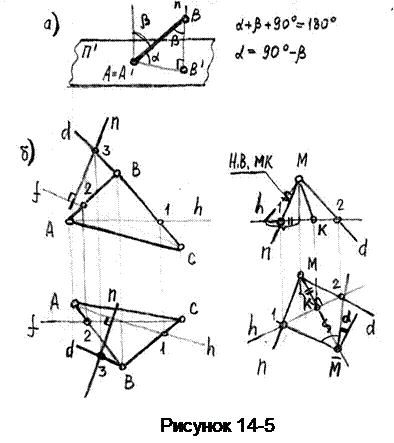
Б (ΔАВС), (рисунок 14-5).
Угол наклона прямой к плоскости можно рассматривать как дополнительный угол до .90°между данной прямой и нормалью к плоскости (рисунок 18-а, угол β).
Для решения задачи из произвольной точки 3 прямой dстроим нормаль n к плоскости Б. Затем определяем угол между двумя пересекающимися прямыми d и n, для чего через произвольную точку М проводим прямые, параллельные d и n.
Определяем натуру угла между ними; угол дополняющий его до 90° будет искомым.
Пример 14. Определить угол между двумя пересекающимися плоскостями Б(α//b) и Д (с´d) (рисунок 14-6).
Натуральная величина угла между двумя плоскостями измеряется линейным углом, дополняющим до 180° угол между перпендикулярами, опущенными из произвольной точки А на данные плоскости (рисунок 14-6а).
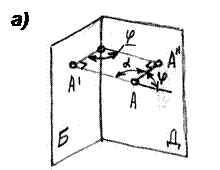
α+φ+90˚=360˚; α+φ=180˚; φ=180˚-α.
Плоские углы φ и αравны линейным углам двух смежных двугранных углов, образованных плоскостями Б и Д.
Алгоритм решения задачи:
1) Вначале находим точку А лежащую на линии пересечения плоскостей (14-6б).
2) Затем восстанавливаем из этой точки перпендикуляры к обеим плоскостям – Б и Д (рисунок 14-6б).
3) Определяем угол между нормалями к плоскостям из Δ1-2-М, построенного по натуральным величинам его сторон засечками (рисунок 14-6в).
Искомый угол φ=180˚-α(рисунок 14-6г).
Источник
