- Все формулы ускорения. Виды ускорения
- Общее понятие
- Криволинейное движение
- Свободное падение
- Угловое ускорение
- Как найти ускорение — определение и формулы расчета в физике
- Что такое ускорение
- Единица измерения
- Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
- Формулы ускорения в физике
- Ускорение: сущность и виды
- Ускорение при движении по окружности
- Готовые работы на аналогичную тему
- Ускоренное движение тела
- Какое бывает ускорение
- Путь, скорость и ускорение
- Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи
- Что такое ускорение?
- Движение по прямой и ускорение
- Полное ускорение и его компоненты при движении тела по кривой
- Угловое ускорение
- Пример решения задачи
Все формулы ускорения. Виды ускорения
Когда в физике изучают механическое движение, то внимание обращают на две главные величины — это скорость и ускорение. Знание их зависимости от времени позволяет определить координату тела в пространстве в любой момент. В данной статье приведем все формулы ускорения для разных его видов.
Общее понятие
Ускорение — это физическая величина. Она определяет, насколько быстро изменяется скорость. Как найти ускорение? Формула приведена ниже:
То есть величина a — это производная скорости по времени. Данное выражение позволяет рассчитать так называемое полное мгновенное ускорение, то есть характеризует величину в данный конкретный момент времени.

На практике чаще всего бывает важно знать не мгновенное, а некоторое среднее ускорение, с которым тело двигалось в течение определенного времени. Рассчитать его можно по такой формуле:
Здесь v2 и v1 — мгновенные скорости в моменты времени t2 и t1 соответственно.
Криволинейное движение
Ускорение определяет величину изменения скорости. У последней варьируется не один параметр. Она может меняться как по направлению, так и по величине. Если тело движется по прямой линии, то вектор скорости сохраняет свое направление. Для такого перемещения полное ускорение определяется исключительно изменением модуля скорости. Его называют касательным или тангенциальным.
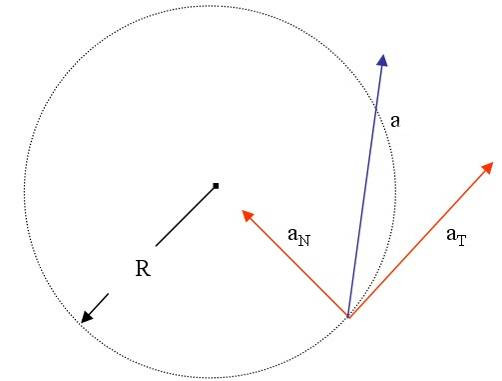
Если же тело перемещается по произвольной криволинейной траектории, то вектор скорости обязательно изменяется. Этот факт приводит к появлению нормальной компоненты ускорения. Рассмотрим подробнее. Раскрывая тему всех формул ускорения, приведем выражение для вычисления нормального ускорения:
Это равенство позволяет сделать два важных вывода:
Чтобы определить модуль полного ускорения, следует воспользоваться такой формулой:
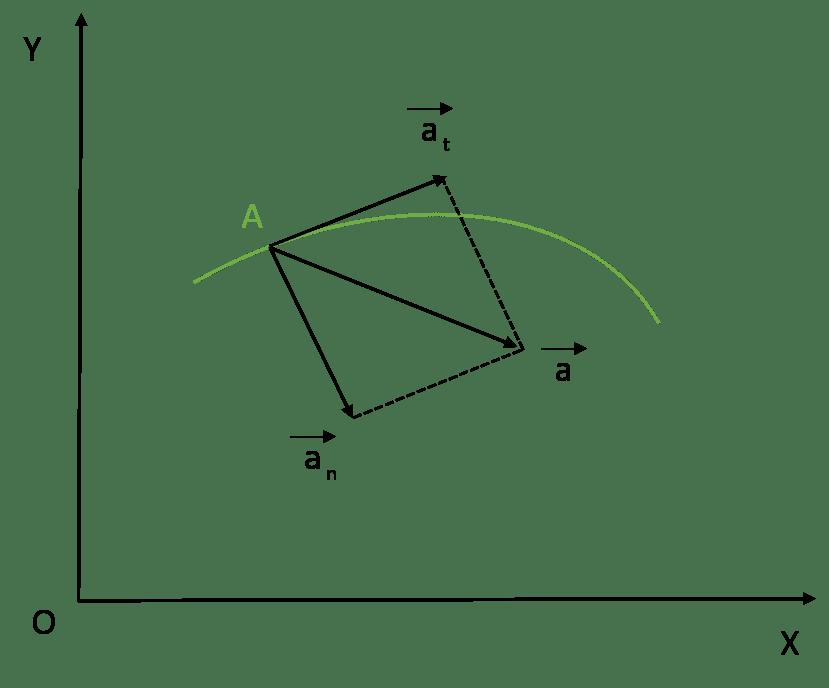
Вектор a определяется как сумма векторов an и at, первый из них направлен перпендикулярно траектории к центру ее кривизны, а второй — по касательной к траектории в сторону изменения модуля скорости.
Свободное падение
Так называют вертикальное движение тела в гравитационном поле планеты, осуществляемое под действием силы тяжести. Как правило, соответствующее ускорение обозначают буквой g. Например, для Земли оно составляет 9,81 м/с2. Приведем все формулы для ускорения g:
Первое из приведенных выражений позволяет определить ускорение g, если известны масса планеты M и ее радиус R. G — это гравитационная постоянная. Эта формула следует из закона Всемирного тяготения Ньютона.
Второе выражение — это всем известное уравнение для силы тяжести F, которая действует на тело массой m.
Наконец, третья формула определяет ускорение через высоту падения h и время падения t тела без начальной скорости. Это выражение является одним из основных в кинематике прямолинейного движения.
Угловое ускорение
Этот вид также нельзя оставить без внимания. Приводя все формулы ускорения, стоит отметить, что угловую величину удобно использовать, когда система вращается вокруг некоторой оси. Она определяет быстроту изменения угловой скорости и выражается в радианах в квадратную секунду. Для определения этого вида ускорения применяют следующие формулы:
α = dω/dt = d2θ/dt2;
Первое равенство показывает, что для определения углового ускорения α следует найти производную от угловой скорости ω по времени либо вторую производную по времени от угла поворота θ.
Вторая строчка — это выражение, которое следует из уравнения моментов. Здесь M — момент силы, которая раскручивает систему, I — момент инерции, который играет роль массы тела во время линейного движения.
Источник
Как найти ускорение — определение и формулы расчета в физике
Что такое ускорение
Ускорение \(\overrightarrow а\) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: \( \begin
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
Где \(a\) — достигнутое ускорение тела, \(S\) — пройденный путь (расстояние), \(t\) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: \(a\;=\;\frac
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: \(a\;=-\;\frac
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
Максимальное ускорение
\(a_
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
\(\overrightarrow
Проекция ускорения
Определение проекции ускорения на ось \(х\) :
\(a_x=\frac
Источник
Формулы ускорения в физике
Вы будете перенаправлены на Автор24
Ускорение: сущность и виды
Под действием различных физических сил тела ускоряют или замедляют свое движение.
Ускорением называют интенсивность изменения скорости движения. Оно характеризует изменение скорости за единицу времени.
В системе СИ ускорение измеряется в метрах в секунду за секунду, иными словами, в метрах в секунду в квадрате ($м/с^2$).
Движение с ускорением, вектор которого не меняется по модулю и направлению, называется равноускоренным.
Определить ускорение при равноускоренном прямолинейном движении можно по формуле:
где $v_1, v_0$ — скорости в начале и в конце рассматриваемого периода времени длительностью $t$.
Отношение изменения скорости к промежутку времени, за который произошло это изменение, называют средним ускорением:
В отличие от равноускоренного, здесь имеют значение направления векторов.
Если начальная скорость больше конечной, происходит замедление, которое в физике также принято называть ускорением, но выраженным с отрицательным знаком.
Мгновенное ускорение — ускорение, развиваемое за очень малый промежуток времени (его длительность стремится к нулю):
Ускорение при движении по окружности
Поскольку ускорение — векторная величина, при движении отличном от прямолинейного оно не остается неизменным даже если модуль скорости не изменяется. В связи с этим ускорение вычисляется из начальной и конечной скоростей по правилам векторной математики, т.е. с учетом изменения направления.
Тело, движущееся по окружности, удобно рассматривать как обладающее двумя ускорениями: тангенциальным ($a_<\tau>$), направленным по касательной к траектории, и центростремительным, направленным к центру ($a_n$). При равномерном движении по окружности тангенциальное ускорение, отражающее мгновенную скорость тела, может быть равно нулю, но центростремительное имеет место даже в этом случае. Поэтому любое движение по криволинейной траектории является движением с ускорением.
Готовые работы на аналогичную тему
Центростремительное ускорение называется также нормальным, тангенциальное — касательным.
Касательное ускорение определяется как мгновенное при движении на очень малое угловое расстояние, когда длина дуги и длина хорды между начальной и конечной точками малоразличимы (сравниваются мгновенные скорости в этих точках).
Формула для определения центростремительного ускорения:
где $v$ — мгновенная скорость, $R$ — радиус траектории.
При движении по искривленной траектории величину результирующего ускорения получают из тангенциального и нормального исходя из теоремы Пифагора:
Такое ускорение называется полным.
Найти ускорение тела, разгоняющегося за 10 с от 5 до 100 км/ч.
В начальный момент времени тело двигалось со скоростью
Скорость в конце интервала:
Подставив числовые значения в формулу, получаем:
Ответ: ускорение составило $ 2,64 м/с^<2>$
Источник
Ускоренное движение тела
Темп изменения скорости называется ускорением. Другими словами, если скорость возрастала на одну и ту же величину в единицу времени, то такое движение называется движение с равномерным ускорением.
Найти ускорение движения тела
Расстояние, ускорение, скорость
Какое бывает ускорение
Ускорение бывает равномерное, положительное и отрицательное.
- Если скорость изменяется (возрастает или убывает) равномерно, то ускорение называется равномерным;
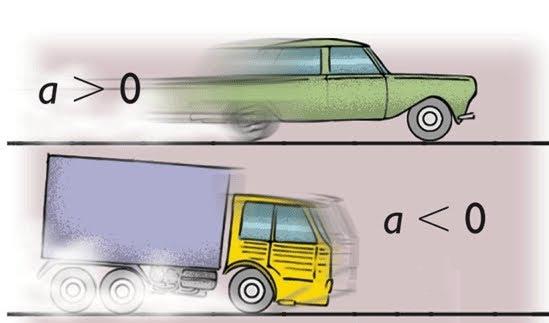
- Если скорость возрастает, то ускорение положительно;
- Если скорость убывает, то ускорение отрицательно.
Формула для нахождения ускорения: a=v/t
Путь, скорость и ускорение
Формула v=at дает соотношение между скоростью, ускорением и временем, а формула S = at 2 /2 дает соотношение между путем, ускорением и временем. До сих пор, однако, мы не имели соотношения между путем S, скоростью и и ускорением а. Один из способов вывести это соотношение заключается в подстановке t 2 , выраженного через v и а, в формулу S = at 2 /2. Решая относительно t формулу v=at, мы получим t=v/a. Возведя обе части в квадрат: t 2 =v 2 /a 2 , подставляя v 2 /a 2 вместо t 2 , имеем
v 2 = 2aS
Скорость автомобиля 90 см/сек. Через 3 сек его скорость равна нулю. Найдите его отрицательное ускорение (темп равномерного уменьшения скорости).
a=-v/t
a=-90/3=-30 см/сек. за 1 сек.
Ответ можно записать и так: 30 см/сек 2 , это будет означать, что автомобиль уменьшает свою скорость на 30 см/сек за каждую секунду.
Источник
Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи
В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.
Что такое ускорение?
Максимально полное определение этой кинематической характеристики можно привести следующее: ускорение — это величина, показывающая быстроту изменения скорости во времени. Речь идет об изменении как модуля, так и направления. Математически ускорение вычисляют так:
Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:
a = (v2 — v1)/(t2 — t1).
Где v2 и v1 — скорости в моменты времени t2 и t1 соответственно.
Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.
Движение по прямой и ускорение
Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.
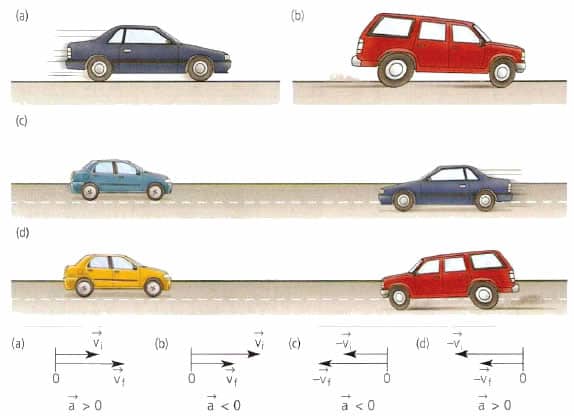
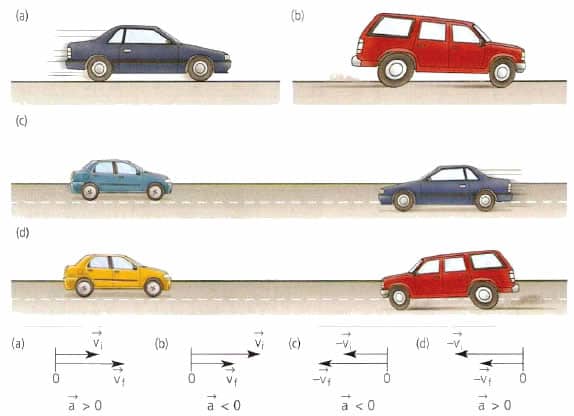
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:
Здесь v0 — некоторая начальная скорость тела, которая может быть также равна нулю, l — пройденный телом путь к моменту времени t. Знак + говорит об ускорении тела, знак — — о его торможении. Важно запомнить, что время t при использовании записанных формул начинает отсчитываться от момента появления у тела постоянного ускорения a. С учетом записанных равенств, формулы модуля ускорения тела принимают вид:
Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).
Полное ускорение и его компоненты при движении тела по кривой
В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:
Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:
Здесь r — радиус кривизны траектории, который в случае вращения по окружности совпадает с радиусом последней.
Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.
Угловое ускорение
Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:
Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.
Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:
Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.
Пример решения задачи
Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:
Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.
Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:
at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.
Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).
Нормальная компонента вычисляется так:
an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.
Теперь можно рассчитать полное ускорение. Оно будет равно:
a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.
То есть, полное ускорение практически полностью образовано нормальной компонентой.
Наконец, ускорение угловое определяется по формуле:
α = at/r = 76/0,2 = 380 рад/с2.
Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.
Источник