Все способы нахождения площади трапеции

Площадь трапеции

Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.

Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.

Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм 2 , см 2 , м 2 и км 2 и так далее.

Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.

Формулы площади трапеции

Площадь любых трапеций

Ⅰ. Площадь трапеции через основания и высоту:

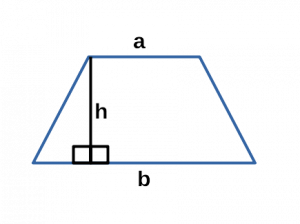
\[ S = \frac <2>\cdot h \]
a,b — основания трапеции;
h — высота трапеции;

Ⅱ. Площадь трапеции через высоту и среднюю линию:

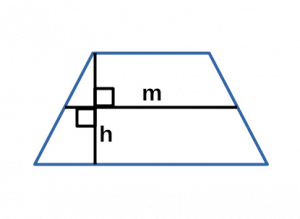
\[ S = mh \]
m — средняя линия трапеции;
h — высота трапеции;

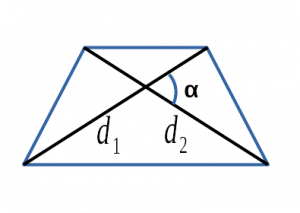
Ⅲ. Площадь трапеции через диагонали и угол между ними:

\[ S =\frac<1><2>d_1d_2 \cdot \sin \alpha \]
\( d_1, d_2 \) ​​- диагонали трапеции;
sin α — синус угла альфа в трапеции;

Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:

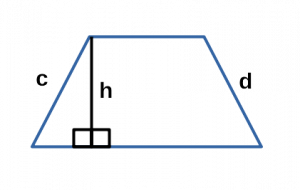
\[ S = \frac<2>h \]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;

Ⅴ. Площадь трапеции через основания и боковые стороны:
\[ S = \frac <2>\cdot \sqrt<2a-2b>)^2> \]
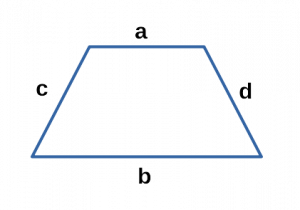
a,b — основания трапеции;
с,d — боковые стороны трапеции;

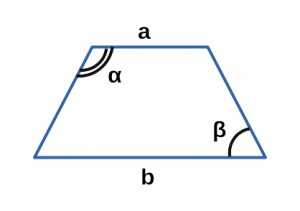
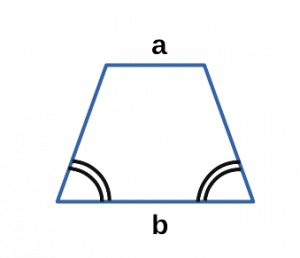
Ⅵ. Площадь трапеции через основания и углы:

a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;

Площадь равнобедренной трапеции

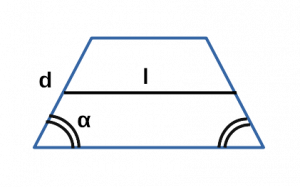
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:

\[ S = ld \cdot \sin α \]

l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

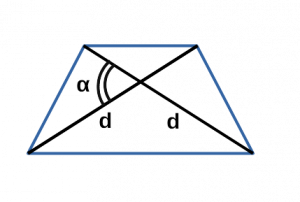
Ⅱ. Площадь трапеции через диагонали и синус угла:

\[ S = \frac <2>\cdot \sin α \]

d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

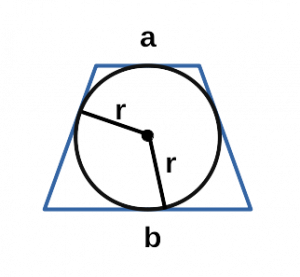
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:

r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

Ⅳ. Площадь трапеции через основания:

a, b — основания равнобедренной трапеции;

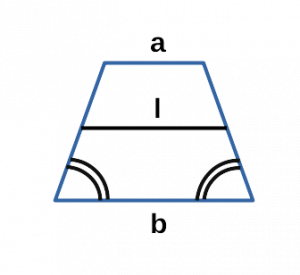
Ⅴ. Площадь трапеции через основания и среднюю линию:

l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

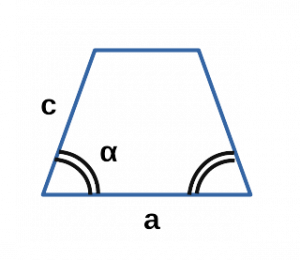
Ⅵ. Площадь трапеции через синус угла и стороны:

\[ S = c \cdot \sin α \cdot (a-c \cdot \cos α) \]

a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;

Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:

r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Определения трапеции

Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.

Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:

• Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
• Равнобедренная / равнобочная / равнобоковая трапеция:
  два угла при основании равны, две боковые стороны равны.
• Прямоугольная / прямаятрапеция: один из углов прямой.

Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.

Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.

Элементы трапеции

Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.

Основание трапеции — это сторона, противолежащая
сторона которой параллельна.

Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.

Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.

Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.

Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.

Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.

Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.

Источник

Как найти площадь трапеции

Что такое площадь трапеции

Трапеция — четырехугольник, две стороны которого, называемые основаниями, параллельны друг другу, а две другие стороны — нет.

Вычисление площади трапеции входит в раздел геометрии, который называется планиметрия и занимается фигурами на плоскости.

Площадь трапеции, как и любой другой геометрической фигуры — это часть плоскости, ограниченная периметром и измеряемая в квадратных единицах.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В формулах основания обозначаются буквами a и b, боковые стороны — с и d.

Способы нахождения площади

Существует более двадцати способов вычисления площади трапеции. Выбор способа расчета зависит от известных данных, которые можно подставить в формулу, и от типа самой трапеции: она может быть равнобедренной (равнобокой) или прямоугольной, тогда задача упростится.

Например, если трапеция равнобедренная, вычислить длину ее сторон можно, разбив ее на прямоугольник и два прямоугольных треугольника.

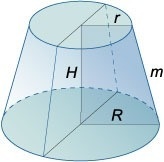
Если трапеция прямоугольная, легко запомнить соотношение ее сторон, пользуясь формулами для усеченного конуса, который образуется при ее вращении вокруг ее боковой стороны, находящейся под прямым углом к основаниям:

Стороны такой трапеции, наглядно видные на схеме, связаны следующим соотношением:

Но большинство формул подходит и для разносторонних трапеций. Если задача практическая и трапеция имеет материальную форму, основания, боковые стороны, высоту и диагонали легко измерить с помощью линейки.

Формулы для вычисления площади равнобедренной и неправильной трапеций

По длине оснований и высоте

Площадь трапеции равна произведению половины суммы оснований на высоту:

Через длины всех сторон (Формула Герона)

Чтобы посчитать площадь через длины сторон, можно воспользоваться следующей формулой:

Существует более простая формула, известная, как формула Герона. Для облегчения ее запоминания вводится р, полусумма всех четырех сторон:

Через диагонали и угол между ними

\(S = \frac<1><2>\times d_ <1>\times d_ <2>\times \sin\alpha.\)

Здесь \(d_<1>\) и \(d_<2>\) — диагонали, а \(\alpha\) — угол, образованный ими.

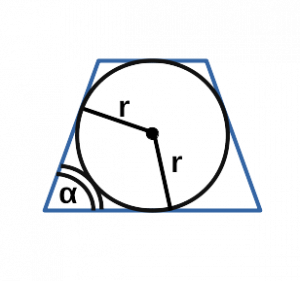
Через радиус вписанной окружности

Вписать окружность в трапецию можно только тогда, когда сумма ее оснований равна сумме боковых сторон.

Площадь любой трапеции можно найти через радиус вписанной окружности, зная длину оснований:

\(S = (a + b) \times r.\)

Площадь равнобокой трапеции также можно найти через круг, вписанный в нее. Для этого нужно знать радиус этого круга, а также угол \(\alpha\) при основании.

Через среднюю линию, боковую сторону и угол при основании

Такой способ нахождения площади подходит только для равнобоких трапеций. В этой формуле средняя линия обозначается буквой m, боковая сторона — буквой с, а угол при основании — \(\alpha\) . Зная длину средней линии и боковой стороны, достаточно найти синус угла и умножить эти значения друг на друга:

\(S = m \times c \times \sin\alpha.\)

Примеры решения задач

Найти площадь трапеции, размер одной диагонали которой равен 6 см, второй — 9 см, а угол между ними — \(30^\circ.\)

Подставим известные данные в формулу:

\(S = \frac<1><2>\times d_ <1>\times d_ <2>\times \sin\alpha\)

Получим: \(S = \frac<1><2>\times 6 \times 9 \times \sin30^\circ = 13,5. \)

Параллельные стороны плоской геометрической фигуры равны 9 и 5 см. Расстояние между ними — 7 см. Найти площадь фигуры.

Подставим известные данные в формулу:

\(S = \frac<1> <2>(a+b) \times h\)

\(S = \frac<1> <2>(9+5) \times 7 = 49.\)

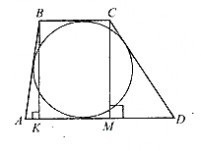
Найти площадь трапеции, если известны длины непараллельных сторон — 13 и 15 см, а также разность длин оснований — 14 см. В трапецию вписана окружность.

Одно из основных свойств трапеции — в нее можно вписать окружность, если сумма оснований равна сумме боковых сторон. Следовательно, если представить две проведенные высоты, как на рисунке, АК + МD = АD — BC = 14.

Поскольку углы К и М являются прямыми, воспользуемся теоремой Пифагора:
\(AB^ <2>= AK^ <2>+ BK^<2>.\)
\(BK^ <2>= AB^ <2>— AK^<2>.\)
\(CD^ <2>= CM^ <2>+ MD^<2>.\)
\(CM^ <2>= CD^ <2>— MD^<2>.\)
\(BK = CM.\)
\(AB^ <2>— AK^ <2>= CD^ <2>— MD^<2>.\)

Подставим числовые значения:
\(13^ <2>— (14 — MD)^ <2>= 15^ <2>— MD^<2>.\)
MD = 9 см.
\(CM^ <2>= CD^ <2>— MD^<2>.\)

Теперь, вычислив высоту, мы можем воспользоваться формулой:

\(S = \frac<1> <2>(a+b) \times h\)

Подставим в нее известные значения, получив:

Источник

Трапеция

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a – h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a – c· cos α – d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

• S – искомая площадь трапеции.
• a, b – основания трапеции.
• c, d – боковые стороны.

Средняя линия трапеции

Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

m =	a + b
	2

2. Формула определения длины средней линии через площадь и высоту:

m =	S
	h

Через длины оснований и высоту

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Формула

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Площадь трапеции через перпендикулярные диагонали

Формула для нахождения площади трапеции через перпендикулярные диагонали: <2>d_1 cdot d_2> , где d₁, d₂ — диагонали трапеции (перпендикулярные).

Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

• S — искомая площадь трапеции.
• a, b — основания трапеции.
• c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

Таблица с формулами площади трапеции

В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.

эскиз	формула
Площадь для всех видов трапеции
1	высота и два основания
2	высота и средняя линия
3	четыре стороны
4	диагонали и угол между ними
5	основания и углы при одном из оснований
Площадь равнобедренной трапеции
6	стороны
7	основание, боковые стороны и угол при основании
8	основание, боковые стороны и угол при основании
9	основания и углы при одном из оснований
10	диагонали и угол между ними
11	средняя линия, боковые стороны и углы между основанием и боковыми сторонами
12	радиус вписанной окружности и угол при основании
13	основания и радиус вписанной окружности
14	основания и углы при одном из оснований
15	основания и боковые стороны
16	основания и средняя линия

Найти площадь равнобедренной трапеции, зная радиус вписанной окружности и угол

Через среднюю линию, боковую сторону и угол при основании

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Пусть a и b основания трапеции. доказать что отрезок, соединяющий середины её диагоналей равен 1/2 * | а – б|?

Возьмем трапецию ABCD

Определим точку М как середину диагонали АС, точку N как середину диагонали BD. Тогда средняя линия трапеции KF будет проходить через точки M и N.

Вспомним свойство средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется полусумме их длин.

Рассмотрим треугольник ACD:

Рассмотрим треугольник BCD

Выразим MN через отрезки MF и NF:

Подставим в формулу значения отрезков MF и NF:

MN = AD/2-BC/2 = (AD-BC)/2

Площадь трапеции через основания и два угла

• Параллельные стороны называются основаниями трапеции.
• Две другие стороны называются боковыми сторонами.
• Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
• Расстояние между основаниями называется высотой трапеции.
• Трапеция, у которой боковые стороны равны, называется равнобокой (или равнобедренной)
• Трапеция, один из углов которой прямой, называется прямоугольной.
• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
• У равнобокой трапеции углы при основании равны.
• У равнобокой трапеции диагонали равны.
• Если трапеция равнобокая, то около нее можно описать окружность.
• Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
• В трапеции середины оснований, точка пересечения диагоналей и продолжения боковых сторон находятся на одной прямой.

Источник