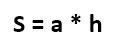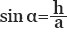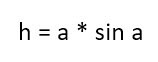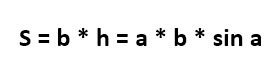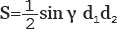Все способы нахождения площади параллелограмма

Площадь параллелограмма

Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.

Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Площадь параллелограмма по основанию и высоте параллелограмма

Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

Площадь параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма по двум диагоналям и углу между этими диагоналями

Площадь параллелограмма по вписанной окружности и стороне

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Площадь параллелограмма по вписанной окружности и углу между сторонами

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади параллелограмма

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	основание и высота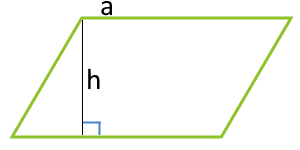
2	сторона и высота, опущенная на эту сторону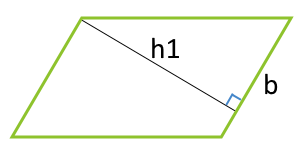
3	две стороны и угол между ними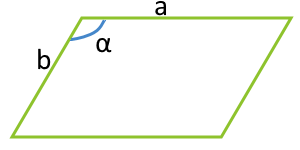
4	диагонали и угол между ними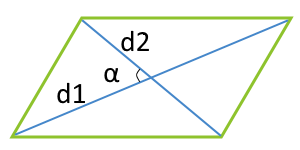
5	вписанная окружность и сторона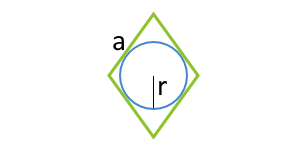
6	вписанная окружность и угол между сторонами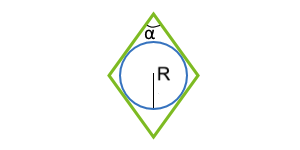

Определения

Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.

Некоторые свойства параллелограмма:

• Сумма углов параллелограмма равна 360 градусов
• Сумма углов, прилегающих к любой из сторон равна 180 градусов
• Противоположные стороны параллельны и имеют одинаковую длину
• Противолежащие углы равны

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Источник

Все формулы площади параллелограмма

1. Формула площади параллелограмма через стороны и углы

a, b — стороны параллелограмма

α , β — углы параллелограмма

Формула площади через стороны и углы параллелограмма, ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

2. Формула площади параллелограмма через сторону и высоту

a, b — стороны параллелограмма

H _b — высота на сторону b

H _a — высота на сторону a

Формула площади через стороны и высоты параллелограмма, ( S ):

3. Формула площади параллелограмма через диагонали и угол между ними

D — большая диагональ

d —меньшая диагональ

α , β — углы между диагоналями

Формула площади через диагонали параллелограмма и угол между ними , ( S ):

Калькулятор — вычислить, найти площадь параллелограмма:

Формулы для параллелограмма:

Источник

Как найти площадь параллелограмма — три основных формулы

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.

Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.

Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.

Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».

Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.

Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.

Формулы для расчета площади параллелограмма

Есть три основных формулы для вычисления площади параллелограмма:

1. если известна длина стороны и высота, проведенная к ней;
2. если известны длины сторон и углы между ними;
3. если известны длины диагоналей и угол между ними.

Теперь о каждом из этих способов подробнее.

Как найти площадь параллелограмма, если известны сторона и высота

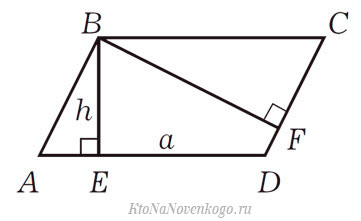
Возьмем для примера такой параллелограмм:

В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.

В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.

И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.

Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:

В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.

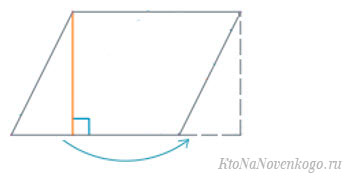
Формула площади параллелограмма, если известны стороны и угол

Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.

Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.

Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:

Соответственно, чтобы посчитать значение высоты надо:

И наша конечная формула для расчета площади будет выглядеть следующим образом:

Как найти площадь параллелограмма через диагонали

Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.

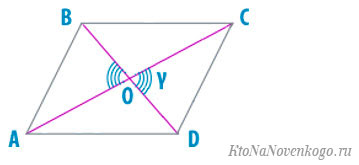
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:

Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.

Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Ну самую простую (основание на высоту) знают все, а вот остальные вспомнить было трудно.

Я еще со школы помню, что можно через окружность вписанную и сторону вычислить. Это будет 2 * на сторону * на радиус окружности. Также есть еще возможность найти по радиусу и углу между сторонами, но эти формулы используются редко, но для каких-то задач возможно пригодятся.

Источник

Площади фигур. Площадь параллелограмма.

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей

одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь

будет равна числу этих квадратов.

Параллелограмм это четырехугольник, у которого противоположные стороны попарно параллельны и

лежат на параллельных прямых.

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус

Воспользуйтесь нашим калькулятором для расчета площади параллелограмма.

Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.

Формулы для определения площади параллелограмма:

1. Площадь параллелограмма по длине стороны и высоте.

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону

2. Площадь параллелограмма по двум сторонам и углу между ними.

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

3. Площадь параллелограмма по двум диагоналям и углу между ними.

где S — Площадь параллелограмма,

a, b — длины сторон параллелограмма,

h — длина высоты параллелограмма,

d₁, d₂ — длины диагоналей параллелограмма,

α — угол между сторонами параллелограмма,

Источник

Нахождение площади параллелограмма: формула и примеры

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

Формула вычисления площади

По длине стороны и высоте

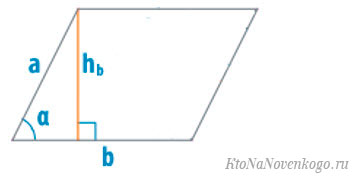
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см 2 .

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см 2 .

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см 2 .

Источник