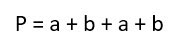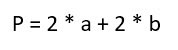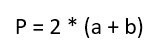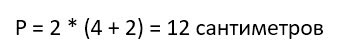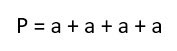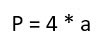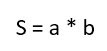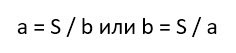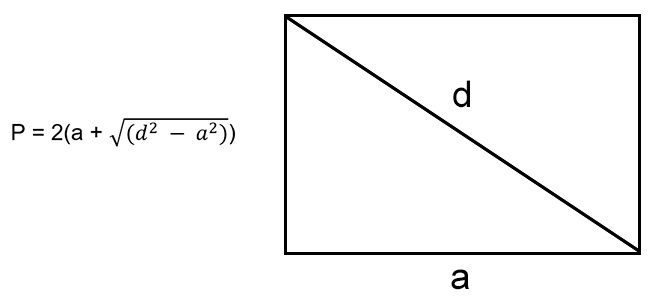Все способы нахождения периметра прямоугольника

Периметр прямоугольника — формулы или способы расчетов

Началом пропедевтики изучения геометрии являются знания, которые учащиеся получают, переходя во 2 класс. Применяя правила умножения, здесь впервые вычисляют периметр прямоугольника.

Переходя в следующий, 3 класс, школьники на основе этой формулы начинают знакомиться с правилами раскрытия скобок.

Как вычислить периметр прямоугольника

Учитывая, что периметр любой фигуры есть сумма длин её сторон, выводят две формы записи для нахождения этой величины.

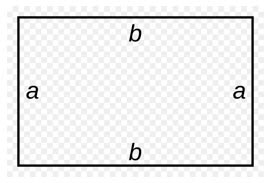
В прямоугольнике противоположные стороны равны, поэтому, обозначив смежные стороны a и b, получают по определению:

откуда после приведения подобных слагаемых, вытекает формула

или, вынося двойку за скобки,

Рассматривая квадрат, как прямоугольник с равными сторонами, получают формулу его периметра:

Стандартный метод

В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.

Задача

Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.

Решение

Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна

P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)

Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.

Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!

Часто длина заданного отрезка измеряется непосредственно.

Нахождение периметра через площадь и одну сторону

При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.

Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.

то есть, соотношение площади и периметра при известной стороне есть

Как найти периметр прямоугольной фигуры

В начальной школе для запоминания принципа детям часто предлагается понятие «неправильного четырёхугольника» (не прямоугольника).

Для нахождения его периметра предлагается рассчитать сумму длин сторон непосредственно, предварительно измерив каждую из них.

Для любой более сложной фигуры производят разбиение, если возможно, на небольшие прямоугольники, с которыми и работают.

Заключение

Современный онлайн калькулятор позволяет ввести значения сторон и задать необходимую точность вычислений, мгновенно производя расчёт и выдавая необходимый результат.

Источник

Периметр прямоугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.

Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.

Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.

Что такое прямоугольник и что такое периметр

Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.

Выглядит прямоугольник соответственно:

А частным случаем прямоугольника является квадрат:

У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.

Как и многие термины в математике, слово «периметр» пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,

Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.

С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.

Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».

Как найти периметр прямоугольника

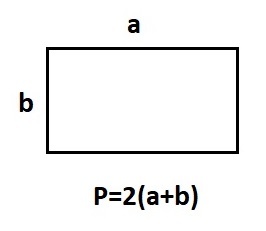
Возьмем для примера такой прямоугольник:

Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.

Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:

С учетом равенства сторон, формулы можно существенно упростить:

Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:

И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.

В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:

Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.

Другие формулы для расчета периметра прямоугольника

Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.

Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:

Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:

Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.

Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:

Вместо заключения

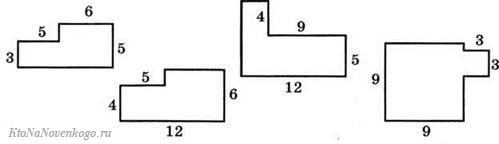
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:

Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их периметры по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.

Вот и все, что мы хотели сегодня рассказать.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Периметр прямоугольника найти просто, а вот со всякими сложными фигурами, у которых стороны криволинейные, вот тут с нахождением правильного решения замучаешься.

Вот это я сейчас в школьную программу геометрии вернулся! На самом деле тема-то легкая, но когда читаешь объяснения, то вообще не сразу понимаешь что к чему.

Источник

Как найти периметр прямоугольника

О чем эта статья:

Основные определения

Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра прямоугольника

Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.

Когда известны все или две соседние стороны

P = a + b + c + d, где a, b, c, d — стороны.

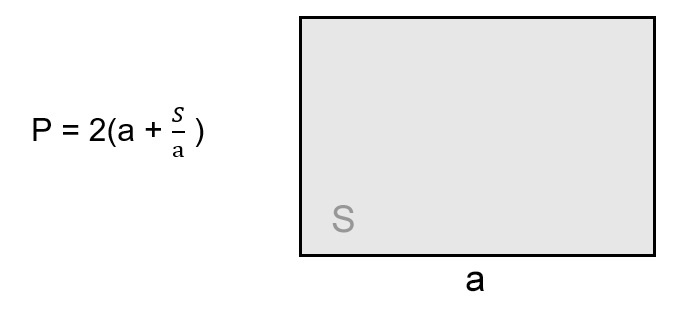
Когда известна любая сторона и площадь

P = 2 * (a + S : a), где a — сторона, S — площадь.

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Когда известна любая сторона и диагональ

P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

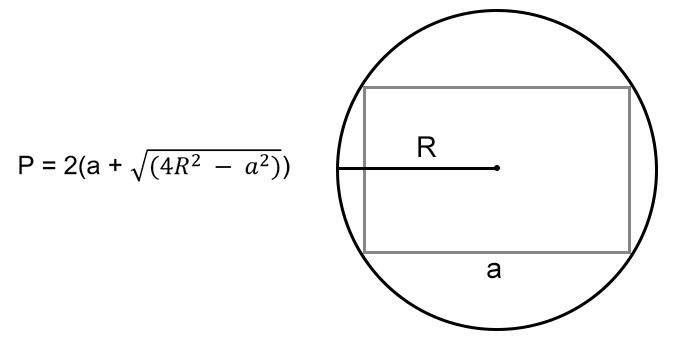
Когда известна одна любая сторона и радиус описанной окружности

P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.

Радиус — отрезок, соединяющий центр и любую точку окружности.

Решение задач

А теперь практиковаться!

1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?

• Если a = 9, то b = 9 + 11;
• Тогда b = 20 см;
• Воспользуемся формулой P = 2 * (a + b);
• P = 2 * (9 + 20);

2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти длину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 60 : 15 = 4;
• Далее подставляем известные переменные в формулу: (15 + 4) * 2 = 38;

А еще можно вот так:

• Воспользуемся формулой P = 2 * (a + S : a);
• P = 2 * (15 + 60 : 15);

Ответ — такой же, 38 м.

3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?

• Если a = 8, то d = 8 *2;
• Тогда d = 16;
• Воспользуемся формулой P = 2 * (a + √(d 2 — а 2 ));
• P = 2 * (8 + √(16 2 — 8 2 ));

Источник

Как найти периметр прямоугольника

Периметр прямоугольника

Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.

Периметр прямоугольника — это сумма длин всех его ребер.

Основные свойства прямоугольника:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• противоположные стороны фигуры равны и параллельны друг другу;
• сумма всех углов равна 360 градусов;
• диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
• диагонали делят фигуру на два одинаковых прямоугольных треугольника;
• по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
• стороны рассматриваемого четырехугольника также являются его высотами;
• точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
• диагональ этого четырехугольника — это диаметр описанной окружности;
• вокруг него всегда можно описать окружность.

Варианты нахождения периметра прямоугольника

По сторонам

Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:

где \(a\) и \(b\) — это две соседние стороны фигуры.

По любой стороне и площади

Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.

Так как площадь прямоугольника — это произведение двух его смежных сторон \((S=a\times b)\) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: \(b=\frac Sa\) .

Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:

По любой стороне и диагонали

В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.

где \(d\) — диагональ прямоугольника, а \(b\) — неизвестная сторона.

Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:

По любой стороне и радиусу описанной окружности

Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:

где \(R\) — радиус описанной окружности.

Тогда формула для расчета P будет выглядеть так:

Примеры решения задач

Задача 1

Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.

Решение:

Применяем самую первую формулу для расчета:

Задача 2

Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 \(см^2\) , одна из его сторон равна 6 см. Вычислить Р фигуры.

Решение:

Берем формулу \(P=2(\frac Sa+a)\) и подставляем известные значения:

Задача 3

Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.

Решение:

Вспоминаем формулу для расчета \(P=2(a+\sqrt)\) и вставляем известные величины:

Задача 4

Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.

Решение:

В этом случае для расчета суммы длин всех сторон применяем формулу \(P=2(a+\sqrt<4R^2-a^2>)\) . Используем известные значения и получаем:

Источник