Восточный способ умножения чисел

Однако как поступить, если при этом приходится делить пополам нечётное число? В этом случае от нечётного числа откидываем единицу и делим остаток пополам, при этом к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет искомым произведением (рисунки: 2, 3).
Иными словами все строки с чётными левыми числами зачёркиваем; оставляем, а затем суммируем не зачёркнутые числа правого столбца.

Для рисунка 2: 192 + 48 + 12 = 252
Правильность приёма станет ясна, если принять во внимание, что:
5 × 48 = (4 + 1) × 48 = 4 × 48 + 48
21 × 12 = (20 + 1) × 12 = 20 × 12 + 12
Ясно, что числа 48, 12, утрачиваемые при делении нечётного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение.
Русский способ умножения и элегантен и экстравагантен одновременно 😉

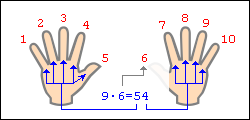
А вот таблица умножение для числа 9 легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для этого числа придумали способ умножения «на пальцах».

Умножение на пальцах — это нечто особенное. Прономеруем пальцы от1 до 10 слева на право. Загибаем палец с номером соответствующим второму множителю и сразу же видим ответ: первая цифра — количество пальцев слева от загнутого, вторая – справа. Все гениальное — просто.

В России мы привыкли умножать числа традиционным способом, которому нас учили в школе, записывая числа-множители столбиком (подробнее про наше умножение ). Однако в азиатских странах, таких как Япония и Китай принято считать иначе. Для созерцательного восточного менталитета важна непременная визуализация. Даже общепризнанные в мире арабские цифры китайцы и японцы записывают иероглифами. Именно с особенностью азиатской графической системы связан японский и китайский способ умножения чисел.

Восточный способ умножения.

Для любознательных: Умножение обозначается знаком [ × ] или [ · ]
Знак [ × ] ввёл английский математик Уильям Оутред в 1631 году.
Знак [ · ] ввёл немецкий учёный Готфрид Вильгельм Лейбниц в 1698 году.
В буквенном обозначении эти знаки упускаются и вместо a × b или a · b пишут ab.

Источник

Способы умножения

Все знают, как умножать в столбик, немного меньше людей знают об умножении линиями, но есть и другие интересные способы.

Умножение чисел — это очень простая операция, фактически, то же самое, что и суммирование. Конечно, пока сами числа не большие.

2х3=2+2+2 (три раза по два) или 24х6=24+24+24+24+24+24 (шесть раз по 24)

То есть, знать таблицу умножения вовсе не обязательно? Да, но с ней удобнее. Например, в случае умножения чисел 235х4596, число 4596 придется сложить 235 раз! Или наоборот, 235 сложить 4596 раз…

Слово «сложить» употреблено не зря. Вот простой способ в этом убедится. Нужно взять листок бумаги сложить его 5 раз в одном направлении, а потом 3 раза в другом. Получится действие 5х3. Считаем получившиеся от сгибания прямоугольники — их 15. Это то же самое, если бы мы взяли 3 полоски ткани (или чего угодно) длинной 5 и сложили вместе.

Как ни крути, а получается — 15!

Необычные способы умножения

В школе нас учат использовать два инструмента: таблицу Пифагора (считается что таблицу умножения придумал именно этот греческий математик) и умножению «в столбик». Это действительно самые эффективные инструменты? Кроме них есть еще несколько интересных способов умножать числа. Может, какой-то из них будет проще и учить таблицу не придется?

По-крестьянски

Использовался для определения площади земельного участка. Например, имеем поле длинной 6 и шириной 5.

Чтобы узнать, сколько будет 6х5 делаем следующее: левое число делим на 2, а правое умножаем на 2, пока от левого числа не останется единица.

2/2= 1 | 10*2=20

4х5=20, все правильно, так же как и 1х20=20

Что происходит при таком способе? Мы разделяем прямоугольник пополам, пока его ширина не станет равняться единице. Делить на два не сложно.

Вот только что будет, если одна из сторон не будет делиться на 2? Будет долгий и не такой уж простой процесс.

6/2=3 | 2*2=4 → 12

3/2=1,5 | 4*2=8 → 12

1,5/2=0,75 | 8*2=16 → 12

Если в левой части четное число — эту строку не считаем, если значение меньше единицы — тоже отбрасываем, остается вторая и третья строка, а это 8+4=12. А если представить, что умножит нужно 173 на 735? Нет, такой способ умножения не самый легкий и простой.

Можно делить/умножать и на 3, но тогда нужно знать таблицу умножения «на три», тогда уж и 5 и 7 и… Да, удобнее выучить ее всю. Также, если будет необходимо перемножить большие числа, процесс будет очень длинным.

Восточный способ

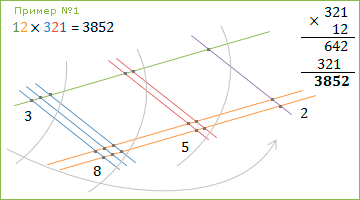
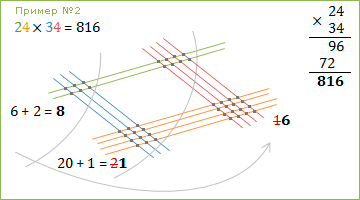
То ли китайский, то ли японский способ умножения, при помощи линий, он же «графический». Его суть состоит в том, что цифры первого числа изображаются в виде параллельных линий, а второго — перпендикулярных им. Количество пересечений и является результатом умножения. То есть, здесь знать таблицу умножения не нужно, достаточно уметь суммировать. Например, так:

2 х 3 и даже 15 х 12

Японский или китайский метод, суть не меняется

Как работает умножение линиями?

Первое число (фиолетовым цветом на картинке) рисуется так: Снизу вверх, слева на право, сначала тысячи, потом сотни, десятки, единицы. Второе число (голубым цветом на картинке) рисуется наоборот: сверху-вниз.

В первом примере все просто 2 и 3. Две линии пересекают 3 другие, получается 6 точек. Во втором, сначала рисуем 15 — единицу (один десяток), потом пять линий изображающих 5 (пять единиц). Потом (12) перпендикулярно ей вторую единицу и 2 линии.

Далее нужно посчитать пересечения, но уже в обратном направлении. Начинать справа. В примере это 10, 7 и 1. Результат складывается в столбик:

Если сравнить с традиционным «столбиком», сперва может показаться, что японско-китайский метод проще…

А что делать, если нужно умножить 10 на 12? Как изобразить «ноль» линией? Никак, он участия не принимает, можно нарисовать его пунктиром и пересечение не считать, все просто…

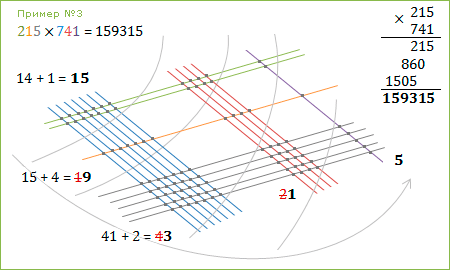
Но вот уже случае 853х951 рисовать и считать точки придется очень много. Старый-добрый столбик опять окажется удобнее. Каждый сам может попробовать перемножить 9878 и 8794 «японским методом» и засечь необходимое время.

Японский метод с нулем

Эта методика не универсальна, совсем не подходит, когда числа достаточно большие, зато ее очень просто объяснить маленьким детям, которые еще не знают таблицу умножения.

Жалюзи

Встречается еще и название «решетки» и индийский метод умножения. Поверить в индийское происхождение проще всего, если вспомнить, кто вообще придумывал эту вашу математику в древности. Итак, чтобы умножить два числа, нужно построить матрицу (если угодно — таблицу, мы же пытаемся быть проще).

Умножаем 45 на 82

Так как в каждом числе по 2 цифры, таблица будет 2х2. Каждую ячейку нежно перечеркнуть по диагонали. Далее записываем слева-на-право, и сверху-вниз цифры 4, 5, 8, 2 напротив каждой ячейки. Начинаем умножать цифры находящиеся напротив друг-друга. 4 на 8, 5 на 8, 4 на 2 и 5 на 2.

Ну вот опять нужна таблица умножения, иначе придется долго складывать числа.

Результаты записываются в ячейки хитрым способом, десятки над диагональю, а единицы — под ней. Но, если значение меньше 10 (то есть это одна, а не две цифры), то вместо десятки верху пишется «ноль», как при умножении 4х5. Но можно оставить поле пустым.

Теперь, чтобы узнать результат, нужно посчитать сумму в каждой диагонали, как показано на картинке. Сверху-вниз:

3

0+2+4=6

8+1=9

0

В результате получаем 3690.

Тоже достаточно просто, только с небольшими значениями, для умножения трехзначных чисел придется рисовать таблицу размером 3х3=9 ячеек.

Какой метод умножения лучше?

Если перепробовать все способы умножения чисел, становится очевидно, что все представленные альтернативные методы умножения — это все варианты знакомого «столбика». Также операции разбиваются на более мелкие: сначала умножение, потом — суммирование.

Только в так называемом китайском/японском способе умножение как таковое не используется (вместо него пересечение линий) и в этом варианте действительно можно обойтись без таблицы умножения, но придется много рисовать, что повышает вероятность совершить ошибку при пересчете точек пересечения.

Есть мнение, что популярность умножения в столбик вызвана именно компактностью записи. Так на умножение требуется меньше бумаги, меньше чернил (да, чернила раньше использовались и тоже стоили денег) и соответственно времени.

Знать нетрадиционные методики интересно и даже полезно, но школьная таблица умножения, все же быстрее, а если вы знаете как умножать в столбик — это удобнее, чем любой другой способ. Если, конечно, не считать калькулятор.

Источник

Способы умножения в разных странах: от древности к современности

Способы умножения в разных странах: от древности к современности

Помните школьные уроки по математике, когда мы учились умножению без калькулятора? В столбик! Достаточно простой способ, не так ли? А вы знали, что в разных странах свои схемы умножения «вручную»? Предлагаю узнать самые популярные способы умножения в разных странах, начиная с древних и заканчивая современными.

Русский способ умножения

Русский способ заключается во всем известном умножении в столбик. Например, возьмем число 1234 и умножим на 56789:

Берем второе число и крайнюю справа цифру (9), умножаем на каждое число из верхнего ряда в порядке справа налево (4, 3, 2 и 1). Результат записываем под каждой цифрой из второго ряда.

Тоже самое делаем со следующей цифрой второго ряда. Но комбинацию чисел записываем уже отступив на одну единицу влево. Смотрите на изображение ниже.

Складываем по столбикам цифры и «сносим» числа вниз. Наш готовый ответ — 70077626.

Японский способ умножения

Японский метод очень похож на китайский. Однако, есть некоторые отличия. Используются не только линии, но и круги. Умножим 12*34:

Смотрим на второй множитель — это двузначное число, поэтом рисуем 2 разделенных круга.

Смотрим на вторую цифру первого множителя (в нашем случае 2) и рисуем два двоичных круга.

Второй множитель состоит из цифр 3 и 4, поэтому делим кружки первого столбика на 3 части, а второго — на 4.

Ответ кроется в количестве частей, которые получились после разделения. Наш результат — 408.

Китайский способ умножения

Основа китайского метода заключается в рисовании линий «сеткой». Преимуществом является графическая визуализация процесса умножения. Основная суть способа — параллельные и перпендикулярные линии представляют те числа, которые перемножаются между собой. Рассмотрим на «живом» примере «25*15»:

Необходимо нарисовать 2 параллельные линии и через некоторое расстояние еще 5 параллельных.

Перпендикулярно им рисуем 1 линию и на небольшом расстоянии еще 5.

Считаем количество точек-пересечений, как указано на схеме.

Если получились двузначные числа, первый знак числа мы прибавляем к «соседнему» с левой стороны. Вторые знаки в числах и являются результатом умножения.

Собираем числа в одно целое и получаем наш ответ: 25*15=375.

Индийский способ умножения

Индийский метод получил название способ Ферроли. Суть способа заключается в перемножении единиц множителей в определенном порядке. На наглядном примере будет понятно, как это сделать. Умножаем 29 на 11:

Перемножаем вторые цифры из каждого числа: 9*1 = 9.

Умножаем первую цифру первого числа на вторую цифру второго числа. Перемножаем вторую цифру первого числа на первую цифру второго числа. Складываем полученные результаты:
2*1 + 9*1 = 11. В данном случае первую цифру оставляем здесь, а вторая уходит на следующую строчку. Здесь остается 1.

Перемножаем первые цифры числе между собой: 2*1 = 2 + 1 (из верхней строчки) = 3.

Собираем число в обратном порядке — 319.

Итальянский способ умножения

Итальянский вариант умножения называется «джелозия» или способ решетки. На самом деле этот метод был изобретен в Индии, но со временем мигрировал в Китай, Аравию и Италию, где и получил свою форму «решетки», напоминающую окно.

Сейчас расскажу, как можно умножить 23*41:

Рисуем прямоугольник и делим его на 4 клетки (в нашем случае, а вообще по клетке на цифру).

Над каждой клеткой подписываем цифры по порядку: 2, 3, 4, 1.

Делим каждую клетку на две части, по диагонали.

Умножаем первые цифры каждого числа (2 на 4), в первом и втором треугольниках пишем 0 и 8.

Умножаем вторую цифру первого числа на первую второго числа (3 на 4), в первом и втором треугольниках пишем 1 и 2.

Умножаем вторые цифры каждого числа (3 на 1), в первом и втором треугольниках пишем 0 и 3.

Умножаем первую цифру первого числа на вторую цифру второго (2 на 1), в первом и втором треугольниках пишем 0 и 2.

Все клетки заполнились и теперь нужно сложить числа в определенной последовательности, как на рисунке ниже. Получаем результат — 943.

Старинные способы умножения

Старинный способ умножения легко осуществить с помощью пальцев. Мы можем умножить любое однозначное число на 9. Необходимо просто загнуть палец, который соответствует умножаемой цифре.

Например, умножаем 9 на 3 и загибаем третий палец левой руки. Считаем количество пальцев ДО загнутого (слева и справа). Слева — это первый знак числа, справа — второй. В нашем случае цифры 2 и 7 дают число 27.

Этим способом можно умножать и двузначные, и трехзначные числа, но по одной цифре из каждого числа, а затем складывать их.

Крестьянский способ умножения

Крестьянский способ заключается в умении делить и умножать любое число на 2. Рассмотрим на примере и умножим 47 на 35:

Пишем оба числа на одной прямой и рисуем между ними вертикальную прямую.

Число с левой стороны делим на 2, а с правой — умножаем на 2. Подобную манипуляцию проводим до момента, пока слева не останется 1.

Необходимо вычеркнуть строки, где слева стоят четные числа.

Числа, которые остались справа складываем и получаем результат. В нашем случае — 1645.

Египетский способ умножения

Египетский способ умножения нравится многим школьникам, так как достаточно прост и занимает меньше всего времени на выполнение вычислений. Необходимо разложить первое число на 3 единицы, а затем умножить каждое из них на второй множитель. Полученные результаты нужно сложить, это и будет искомое число.

Кому непонятно, смотрим на пример. Умножаем 13 на 238:

Чтобы получить 13 посредством сложения трех единичных цифр, нужно взять 1, 4 и 8.

Умножаем каждую из цифр на второй множитель (238).

1*238 = 238
4*238 = 952
8*238 = 1904.

Складываем полученные числа и получаем 3094 (238+952+1904).

Умножить на пальцах многозначные числа сложно, поэтому проще всего воспользоваться одним из вышеописанных методов. Мне, например, больше всех нравится русский и китайский способы. Они легкие и интересные.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-473694

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

ЕСПЧ запретил учителям оскорблять учеников

Время чтения: 3 минуты

Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ

Время чтения: 1 минута

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник