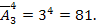Размещения с повторениями
«Опять восьмёрка!» — горестно воскликнул председатель клуба велосипедистов, взглянув на погнутое колесо своего велосипеда. «А всё почему? Да потому, что при вступлении в клуб мне выдали билет за номером 008. И теперь месяца не проходит, чтобы то на одном, то на другом колесе не появилась восьмёрка. Надо менять номер билета. А чтобы меня не обвиняли в суеверии, проведука я перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые ни восьмёрка, ни нуль не входят».
Сказано – сделано, и на другой день он заменил все билеты. Сколь членов было в клубе, если известно, что использованы все трёхзначные номера, не содержащие ни одной восьмёрки и ни одного нуля?
Для решения этой задачи определим сначала, сколько будет однозначных номеров. Ясно, что таких номеров будет восемь: 1 2 3 4 5 6 7 9.
А теперь найдём все двузначные номера, для чего возьмём любой из найденных однозначных номеров и припишем к нему любую из восьми цифр:
11 12 13 14 15 16 17 19
21 22 23 24 25 26 27 29
31 32 33 34 35 36 37 39
41 42 43 44 45 46 47 49
51 52 53 54 55 56 57 59
61 62 63 64 65 66 67 69
71 72 73 74 75 76 77 79
91 92 93 94 95 96 97 99
Очевидно, двузначных номеров будет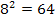 
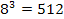
. Но за каждым из них снова можно поставить любую из восьми допустимых цифр. В результате получим 
трёхзначных номеров. Значит, в клубе было 512 велосипедистов.
Задача о велосипедистах относится к следующему типу задач. Даны предметы, относящиеся к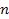 
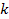
различным видам. Из них составляют всевозможные расстановки по 
предметов в каждой, при этом в расстановки могут входить и предметы одного вида, а две расстановки считаются различными, если они отличаются друг от друга или видом входящих в них предметов, или порядком этих предметов. Надо найти общее число таких расстановок.
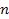
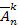
Расстановки описанного типа называются k— размещениями с повторениями из элементов видов и обозначается 
.
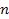
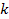
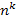
Естественно предположить, что если число видов равно , а в каждое размещение входит элементов, то можно составить 
размещений с повторениями. Итак,
Пример 8. Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены оценки, если известно, что никто из них не получил неудовлетворительную оценку?
Р е ш е н и е. В данном случае у преподавателя три вида оценок: отл., хор., удовл.; при этом все четыре студента могут получить оценку хорошо или отлично; два из них – отл. и два – удовл. и т.д. Имеем размещения с повторениями 
Источник
Восемь студентов сдают экзамен сколькими способами
пЮЕОШ ЮБУФП Ч ТЕБМШОПК ЦЙЪОЙ чБН РТЙИПДЙФУС ТЕЫБФШ РТПВМЕНЩ УМЕДХАЭЕЗП ФЙРБ: ЛБЛ ЙЪ НОПЦЕУФЧБ, УПУФПСЭЕЗП ЙЪ n ЬМЕНЕОФПЧ, ЧЩВТБФШ ХРПТСДПЮЕООПЕ РПДНОПЦЕУФЧП ЙЪ m ЬМЕНЕОФПЧ. оБРТЙНЕТ, ЛБЛ ТБУУБДЙФШ ЪБ РТБЪДОЙЮОЩН УФПМПН 12 ЗПУФЕК, ЕУМЙ ЧУЕЗП 15 НЕУФ ?
пртедемеойе 1.3.1
хРПТСДПЮЕООПЕ m — ЬМЕНЕОФОПЕ РПДНОПЦЕУФЧП НОПЦЕУФЧБ ЙЪ n ЬМЕНЕОФПЧ ОБЪЩЧБЕФУС тбънеэеойен ЙЪ n ЬМЕНЕОФПЧ РП m.
фептенб 1.3.1
юЙУМП ТБЪНЕЭЕОЙК НОПЦЕУФЧБ ЙЪ n ЬМЕНЕОФПЧ РП m ТБЧОП 
1-К ЬМЕНЕОФ НПЦОП ЧЩВТБФШ n УРПУПВБНЙ,
2-К — (n — 1) УРПУПВПН,
m-К — (n — (m — 1)) УРПУПВБНЙ.
уМЕДПЧБФЕМШОП, ПВЭЕЕ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ ХРПТСДПЮЕООПЕ РПДНОПЦЕУФЧП ВХДЕФ ТБЧОП n (n — 1) . (n — (m — 1)).
хНОПЦЙН Й ТБЪДЕМЙН ДБООПЕ ЧЩТБЦЕОЙЕ ОБ (n — m)!:
пвпъобюеойе: 
уЙНЧПМ 
ФБЛ Й ЮЙФБЕФУС: «юЙУМП ТБЪНЕЭЕОЙК ЙЪ n РП m».
умедуфчйе 1.3.1
m ТБЪМЙЮОЩИ РТЕДНЕФПЧ РП n НЕУФБН НПЦОП ТБУУФБЧЙФШ 
УРПУПВБНЙ.
ч ЮБУФОПУФЙ, РТЙЗМБЫЕООЩИ чБНЙ ЗПУФЕК НПЦОП ТБУУБДЙФШ 
УРПУПВБНЙ.
ъбдбюб 1.3.1 уФХДЕОФХ ОЕПВИПДЙНП УДБФШ 4 ЬЛЪБНЕОБ Ч ФЕЮЕОЙЕ 10 ДОЕК. уЛПМШЛЙНЙ УРПУПВБНЙ НПЦОП УПУФБЧЙФШ ЕНХ ТБУРЙУБОЙЕ ЬЛЪБНЕОПЧ? (рТЕДРПМБЗБЕФУС, ЮФП Ч ДЕОШ УДБЕФУС ФПМШЛП ПДЙО ЬЛЪБНЕО.)
тЕЫЕОЙЕ ДБООПК ЪБДБЮЙ УЧПДЙФУС Л ПРТЕДЕМЕОЙА ЮЙУМБ УРПУПВПЧ ТБУУФБОПЧЛЙ 4-И ТБЪМЙЮОЩИ РТЕДНЕФПЧ РП 10 НЕУФБН. уМЕДПЧБФЕМШОП, ЮЙУМП УРПУПВПЧ УПУФБЧЙФШ ДБООПЕ ТБУРЙУБОЙЕ ТБЧОП:
ъбдбюб 1.3.2 уЛПМШЛП УМПЧ НПЦОП ПВТБЪПЧБФШ ЙЪ ВХЛЧ УМПЧБ жтбзнеоф, ЕУМЙ УМПЧБ ДПМЦОЩ УПУФПСФШ: Б) ЙЪ 8 ВХЛЧ; В) ЙЪ 7 ВХЛЧ; Ч) ЙЪ 3 ВХЛЧ? (нБФЕНБФЙЛБ РПД УМПЧПН РПОЙНБЕФ РТПЙЪЧПМШОЩК ОБВПТ ВХЛЧ).
Б) n = 8, m = 8. юЙУМП УРПУПВПЧ ТБЧОП 
= 8!.
В) n = 8, m = 7. юЙУМП УРПУПВПЧ ТБЧОП 
= 8!.
Ч) n = 8, m = 3. юЙУМП УРПУПВПЧ ТБЧОП 
= 336.
ъбдбюб 1.3.3 дЕУСФШ ЛТЕУЕМ РПУФБЧМЕОЩ Ч ТСД. уЛПМШЛЙНЙ УРПУПВБНЙ 2 ЮЕМПЧЕЛБ НПЗХФ: Б) УЕУФШ ОБ ОЙИ; В) УЕУФШ ТСДПН; Ч) УЕУФШ ФБЛ, ЮФПВЩ НЕЦДХ ОЙНЙ ВЩМП, РП ЛТБКОЕК НЕТЕ, ПДОП РХУФПЕ ЛТЕУМП?
Б) n = 10, m = 2. юЙУМП УРПУПВПЧ 
= 90.
В) пВПЪОБЮЙН ЬФЙИ ДЧХИ ЮЕМПЧЕЛ ХУМПЧОП и Й х.
ъБНЕФЙН, ЮФП ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ ПОЙ УЙДЕМЙ ТСДПН Й и ВЩМ УРТБЧБ ПФ х, ТБЧОП 9. бОБМПЗЙЮОП, ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ, и ВЩМ УМЕЧБ ПФ х, Й ПОЙ УЙДЕМЙ ТСДПН, ФПЦЕ — 9. (ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ НЩ ЧЩВЙТБЕН НЕУФП ФПМШЛП ДМС и.) уМЕДПЧБФЕМШОП, ПВЭЕЕ ЮЙУМП УРПУПВПЧ: 9 + 9 = 18.
Ч) дМС РПМХЮЕОЙС ПФЧЕФБ ОБ РПУФБЧМЕООЩК ЧПРТПУ, ДПУФБФПЮОП ЧПУРПМШЪПЧБФШУС ТЕЪХМШФБФБНЙ, РПМХЮЕООЩНЙ Ч РХОЛФБИ Б) Й В). фП ЕУФШ, ЙЪ ПВЭЕЗП ЮЙУМБ УРПУПВПЧ ТБУУБДЙФШ 2-И ЮЕМПЧЕЛ РП 10 ЛТЕУМБН ЧЩЮЕУФШ ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ ПОЙ УЙДЕМЙ ТСДПН: 90 — 18 = 72.
ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.
ъбдбюб 1.3.1(у) чПУЕНШ НБМШЮЙЛПЧ ЧПДСФ ИПТПЧПД. ъБФЕН Л ОЙН РТЙУПЕДЙОСАФУС ЕЭЕ РСФШ ДЕЧПЮЕЛ. уЛПМШЛЙНЙ УРПУПВБНЙ ДЕЧПЮЛЙ НПЗХФ ЧУФБФШ Ч ЛПМШГП, ЕУМЙ ОЙЛБЛЙЕ ДЧЕ ДЕЧПЮЛЙ ОЕ ДПМЦОЩ УФПСФШ ТСДПН?
ъбдбюб 1.3.2(у) уЛПМШЛП ЮЕФЩТЕИЪОБЮОЩИ ЮЙУЕМ НПЦОП УПУФБЧЙФШ, ЙУРПМШЪХС ГЙЖТЩ 1, 2, 3, 4, 5; ЕУМЙ ЮЙУМБ ДПМЦОЩ ВЩФШ ОЕЮЕФОЩЕ Й РПЧФПТЕОЙК ГЙЖТ ВЩФШ ОЕ ДПМЦОП?
ъбдбюб 1.3.3(у) дПЛБЪБФШ, ЮФП ЮЙУМП ФТЕИВХЛЧЕООЩИ УМПЧ, ЛПФПТЩЕ НПЦОП ПВТБЪПЧБФШ ЙЪ ВХЛЧ, УПУФБЧМСАЭЙИ УМПЧП зйрпфеохъб, ТБЧОП ЮЙУМХ ЧУЕИ ЧПЪНПЦОЩИ РЕТЕУФБОПЧПЛ ВХЛЧ, УПУФБЧМСАЭЙИ УМПЧП ртйънб.
© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002
Источник
Помогите с задачей по комбинаторике
Задача 1. Восемь студентов сдают экзамен по теории вероятностей. Сколькими способами им могут быть поставлены оценки, если известно, что они могут получить только «хорошо» или «отлично»?
Задача 2. Солькими способами можно выбрать старосту и профорга в группе из 20 студентов?
Задача 1: если Иванов получил 4, остальные 5 и Петров получил 4 — остальные 5 считается за один способ, а не за 2, то:
Число возможных сочетаний с повторениями равно:
С из (n+k-1) по k, в нашем случае n = 2, k = 8, n+k-1 = 9
Число сочетаний с повторениями равно 9!/(8!) = 9.
Если это считается за 2 разных способа, то ответ 256 способов
Задача 2.
Формула для второй задачи совсем не такая. Привожу вывод формулы для второй задачи (но не вывод приведенной тобой формулы) .
Допустим, первый студент — староста. Профорг может быть вторым, третьим, четвертым. двадцатым студентом (всего 19 вариантов при условии, что первый студент — староста) .
Теперь допустим, что староста — второй студент. Профорг может быть 1,3,4,5..20 (еще 19 вариантов) .
Аналогично, если староста третий студент, 4,5,6. 20 — каждый раз по 19 вариантов.
Т. е. всего возможных вариантов 19*20 = 380.
Можешь убедиться, что по приведенной тобой формуле ответ получится вдвое меньше (т. к. по этой формуле считают число сочетаний — т. е. по этой формуле варианты первый — староста, второй — профорг и первый — профорг, второй — староста считаются за один вариант) .
Тебе нужно использовать формулу С = 20!/(20-2)! (а на 2! уже не делить)
Источник
Восемь студентов сдают экзамен сколькими способами
Комбинаторика для начинающих. МФТИ. Разбор ряда задач недель 2-3
Эти недели были о тех самых четырёх формулах сочетания и размещения.
В семье семеро детей: старший −мальчик, дальше − девочка, девочка, мальчик, мальчик, мальчик и младшая − девочка. Сколькими способами родители могут выбрать имена, если они выбирают из 10 мужских и 13 женских имен и хотят, чтобы имена не повторялись?
Ответ: 8648640.
Решение: можно отвлечься на перечисление детей по возрасту. Не стоит. Соль в их количестве и условии различия имён. Все. Следовательно, обращаемся к числу размещений без повторений, а по правилу умножения размещению 4 мужских имён из 10 известных соответственно 3 женских из 13.
Жених и невеста выбирают трехъярусный свадебный торт. На выбор имеются 5 типов ярусов (бисквитный, йогуртовый, чизкейк и т.д.). Сколько различных тортов может предложить кондитер, если бисквитных ярусов может быть не больше двух, а ярусов любого другого типа не больше одного?
Ответ: 72.
Решение: используем правило сложения и суммируем результаты по трём вариантам — бисквитных ярусов нет, он один, их два.
Если их нет, мы просто размещаем по трём слоям четыре типа. Нам нельзя иметь более одного одинакового слоя из оставшихся. Это размещение без повторений из 4 по 3. Равно 24.
Один ярус может быть занят 3 способами, кроме того, каждому варианту соответствует размещение из 4 уже по 2. Это 3*12=36.
Наконец, бисквитных ярусов два. Они так же могут быть в составе торта 3 способами (чисто интуитивно 1-2, 2-3, 3-1) и им соответствует размещение уже из 4 по 1. 3*4=12.
Итого 24+36+12=72.
В университете десятибальная система оценок: 1−2 −»неудовлетворительно», 3−4 − «удовлетворительно», 5−7 − «хорошо» и 8−10 −»отлично». Сколькими способами можно поставить оценки 5 студентам, если известно, что экзамен сдали все (т.е. нет неудовлетворительных оценок)?
Ответ: 32768.
Решение: задача уже на размещение с повторениями. Ведь оценок у нас хоть сколько, а студенты разные. Здесь варианты 88889 и 88988 это не одно и то же.
Если неудовлетворительных оценок нет, но мы рассматриваем лишь 8 вариантов оценивания, а не 10. И «разместить» эти оценки мы должны по 5 студентам. С возможными повторениями. То бишь, это 8^5.
Группа из 8 студентов пришла в столовую. Сколькими способами они могут занять очередь друг за другом, если Маша и Таня хотят стоять рядом, а Коля не хочет быть последним?
Ответ: 8640.
Решение: Машу и Таню разделять нельзя — они, хоть убей, должны стоять вместе. Давайте для удобства считать, что они японские студентки в коротких юбках и вдвоем пилотируют огромного робота. Можно сказать, что из 8 мест становится 7, так как студентов у нас как будто стало 7.
Но у Коли нет варианта встать на последнее место из 7. У него вариантов вообще 6 — все, кроме последнего.
У всех остальных нет подобных заоморочек. На остальные оставшиеся ребята могут разместиться 6! способами — не 7!, т.к. Коля явно очень голоден и последним в очереди не будет.
Уточним. Маша и Таня могут поменяться местами между собой. Поэтому нам надо не просто умножить 6 на 6!, но и ещё на 2 — есть большая разница между тем, кто пилотирует робота и тем, кто находиться за прицелом и ведёт огонь по вражеским силам. Поэтому 6*6!*2.
У королевы есть 12 одинаковых зеркал. Сколькими способами их можно повесить в 8 разных залах замка так, чтобы в каждом зале было хотя бы одно зеркало?
Ответ: 330.
Решение: внимательно прочитайте — ХОТЯ БЫ одно зеркало. То есть, или одно или два. Здесь нельзя вслепую выбрать сочетание (а порядок не важен и количество зеркал ограничено) 8 из 12. Нет.
Залов меньше, чем зеркал. Очевидно, будут залы с не одним зеркалом.
«Первые восемь» зеркал мы уже, давайте считать, повесили. Уточнение — да, залы разные, но сами зеркала одинаковые. Эти восемь взяли и повесили и, как потом не меняй их местами, суть не меняется.
А вот оставшиеся зеркала это уже другой вопрос. Их 4.
У нас есть 4 оставшихся зеркала. И 8 залов. Мы не обязаны раскидывать эти зеркала равномерно или через раз или ещё как. Мы вообще можем их все отнести в один зал. Это тонкий момент — если мы эти четыре зеркала можем отнести в один зал, то этот зал ПОВТОРЯЕТСЯ. Но при этом порядок тут не имеет значения.
Как вы уже догадываетесь — это сочетание с повторениями. Надо выбрать, в какой из восьми залов нести четыре зеркала. То есть, тут мы выбираем, по сути зал. Они разные, а зеркала одинаковые. Стало быть, это сочетание из 8 по 4 с повторами.
Сколькими способами в течение 5 дней можно выбирать на дежурство по 4 ученика из класса в 20 человек так, чтобы каждый день состав дежурных был разным?
Ответ: скрин.
Решение: легче, чем кажется. Без привязки к дням — как можно выбрать дежурных? Сочетание без повторений из 20 по 4. А дальше? А дальше просто из каждого нового дня вычитаем вариант, который был вчера. А затем это все умножить, ведь надо знать количество способов всего. И обратите внимание, как ловко сочетания тут свернулись в размещения.
Источник
