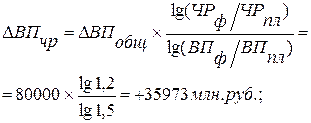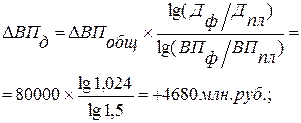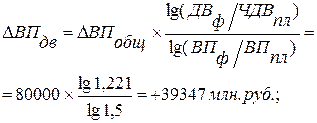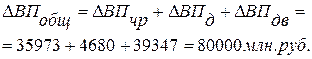Влияние факторов логарифмическим способом

Способ логарифмирования в анализе хозяйственной деятельности — Анализ хозяйственной деятельности предприятия

В нашем примере (см. табл. 6.1) расчет проводится следующим образом:

Для расчета влияния факторов в кратных и смешанных моделях используются следующие рабочие формулы.

Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или другой вычислительной техники. При этом достигается более высокая точность расчетов.

6.7. Способ логарифмирования в анализе хозяйственной деятельности

Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом.

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).

Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f = хуz. Прологарифмировав обе части равенства, получим

Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:

Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.

Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели:

Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.

Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:

Знание сущности данных приемов, области их применения, процедуры расчетов — необходимое условие квалифицированного проведения количественных исследований.

Источник

Логарифмический метод

Обозначим индексами 1 и 0 данные, относящиеся к отчетному и базовому периодам соответственно.

В соответствии с рассматриваемой моделью можно записать:

Отметим, что логарифм здесь может быть любым — натуральным, десятичным или по любому другому основанию. Домножим обе части на ?z и разделим на lnz1z0. Получим:

Итак, прирост результативного показателя распределяется между факторами пропорционально логарифмам их изменения. Особенность метода в том, что при его использовании не требуется установления очередности действия факторов. Недостаток же заключается в том, что действует этот метод только для кратных и мультипликативных моделей. Пример 2.4 иллюстрирует использование логарифмического метода для анализа влияния факторов на изменение результативного показателя. Пример 2.4.

Анализ показывает, что направленность действий факторов противоположная, поэтому влияние каждого из них на изменение результативного фактора отчасти взаимно компенсируется. Задача 3 детерминированного факторного анализа представляет собой оценку влияния относительного изменения факторов на относительное изменение результативного показателя, т.е. определение отношения величины прироста, вызванного изменением любого фактора, к величине результативного показателя за базисный период в процентах. Она решается с помощью индексного метода и будет рассмотрена в разделе 2.7.4. Заканчивая раздел, отметим, что детерминистский подход достаточно распространен в анализе финансово-хозяйственной деятельности предприятий, поскольку позволяет выявить множество связей между факторами, влияющими на деятельность предприятия. Вместе с тем принципиальным недостатком детерминированного подхода является то, что он не позволяет разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели. Смысл данного утверждения совершенно очевиден. Дело в том, что любое предприятие работает в условиях действия множества факторов; объединить эти факторы в какую-либо модель, тем более жестко детерминированную, ни теоретически, ни практически не представляется возможным. Поэтому любое факторное разложение является весьма и весьма условным. Для примера приведем две модели, достаточно широко распространенные в факторном анализе:

где Т — товарооборот (выручка от реализации); Ч — численность работников; В — выработка на одного работника; Ф — фондоотдача; ОС — величина основных средств. Предположим, что проводится факторный анализ динамики изменения товарооборота с использованием этих двух моделей. Для этого необходимо построить следующие факторные разложения:

Из самой сути факторного анализа понятно, что общее приращение товарооборота в обеих моделях одно и то же, т.е.

Источник

Способ логарифмирования в экономическом анализе

Сущность, сфера применения и отличительные черты способа логарифмирования. Алгоритмы расчета влияния факторов этим способом

Способ логарифмирования применяется для измерения влияния факторов только в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечиваетсяболее высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяетсяпоровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяетсяпропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом егопреимущество, анедостаток — в ограниченности сферы его применения.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста(снижения).

Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов; f=xyz. Пролагарифмировав обе части равенства, получим

Учитывая,что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:

Или

Разделив обе части равенства на и умножив наполучим:

,но ,

Отсюда влияние факторов определяется следующим образом:

; ; .

 Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.

Используя данные табл.7.1, вычислим прирост валовой продукции за счет количества работников (КР), и среднегодовой выработки (ГВ) по факторной модели ВП =КРГВ:

=80000=+35 973 руб.;

=80000= +44 027 руб.

Проверка: =35973+44027=80000 руб.

Сравнив полученные результаты расчета влияния факторов разными способами но данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов. Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей таблицы (табл.7.4):

Сравнительная характеристика способов детерминированного факторного анализа

Источник

Способ логарифмирования в анализе хозяйственной деятельности

Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния фактора на уровень результативного показателя. В этом его преимущество, а недостаток – в ограниченности сферы применения.

В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).

Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f =xyz. Прологарифмировав обе части равенства, получим

.

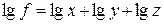
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:

;

.

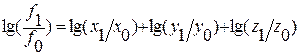
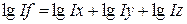
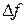
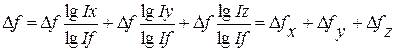
Разделив обе части равенства на lgIf и умножив на , получим:

.

Отсюда влияние факторов определяется следующим образом:

; ; .

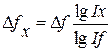
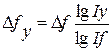
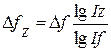
Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели:

Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.

Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:

Прием	Модели
Мультипли-кативные	Аддитивные	Кратные	Смешанные
Цепной подстановки	+	+	+	+
Индексный	+	—	+	—
Абсолютных разниц	+	—	—	Y = a(b – c)
Относительных разниц	+	—	—	Y = (a – b)c
Пропорционального деления (долевого участия)	—	+	—	Y = a/åxi
Интегральный	+	—	+	Y = a/åxi
Логарифмический	+	—	—	—

Знание сущности данных приемов, области их применения, процедуры расчетов – необходимое условие квалифицированного проведения количественных исследований

Источник