Виды выборочного наблюдения по способу организации

Раздел 1. Теория статистики

Цель: сформировать представление о способах решения задач, которые возникают при использовании выборочного наблюдения.

Задачи: познакомить студентов с методикой различных видов статистического наблюдения, оценки надежности выборочных показателей с учетом их случайной ошибки

Оглавление

4.1. Особенности выборочного наблюдения. Генеральная и выборочная совокупности

Выборочное наблюдение – это вид несплошного наблюдения, которое обеспечивает отбор в случайном порядке части единиц совокупности и возможность последующего распространения полученных данных на всю совокупность единиц.

Исходный массив данных называется генеральной совокупностью. Часть единиц генеральной совокупности, которая непосредственно обследуется при выборочном наблюдении, представляет собой выборочную совокупность. Числовые характеристики генеральной совокупности (средняя, дисперсия и др.) называются параметрами генеральной совокупности.

Организационными вопросами выборочного наблюдения являются: обоснование границ генеральной совокупности; единица отбора; единица наблюдения; способы отбора.

4.2. Виды и способы отбора. Виды выборочного наблюдения

По способу организации различают следующие основные виды выборочного наблюдения: собственно-случайная (простая) выборка; типическая (расслоенная, стратифицированная, районированная); серийная (гнездовая); многоступенчатая; многофазная.

При любом виде выборки отбор единиц производится тремя способами: случайный отбор (жеребьевка, таблица случайных чисел); отбор единиц по какой-либо схеме (единицы упорядочивают таким образом, чтобы это было не связано с изучаемыми свойствами; далее проводится механический отбор единиц); сочетание первого и второго способов.

Простая собственно-случайная выборка проводится из всей массы единиц совокупности без предварительного разделения ее на какие-либо группы. Применяется индивидуальный отбор единиц, т. е. единица отбора совпадает с единицей наблюдения. Типическая, (районированная, стратифицированная) выборка используется в случае, когда генеральная совокупность неоднородна и это влияет на размер изучаемого признака. Серийная выборка (кластерный или гнездовой отбор) – это способ формирования выборки, при котором единица отбора состоит из группы или гнезда более мелких единиц, называемых элементами. Многоступенчатая выборка применяется, когда имеют место несколько стадий отбора (ступеней отбора). При этом каждая стадия имеет свою единицу отбора. Число ступеней отбора определяется числом типов единиц отбора и на последней ступени единица отбора совпадает с единицей выборочной совокупности. Многофазная выборка характеризуется тем, что она также включает несколько ступеней отбора, но на всех ступенях сохраняется одна и та же единица отбора (в отличие от многоступенчатой).

Особым видом выборочного наблюдения является моментное наблюдение – это выборочное во времени наблюдение. Объектом выборки являются отрезки времени. Поэтому понятие генеральной и выборочной совокупности относится не к совокупности единиц, а ко времени наблюдения.

4.3. Определение ошибки выборочного наблюдения. Средняя и предельная ошибки выборочного наблюдения

Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности. Различают систематические и случайные ошибки выборки. Случайные ошибки выборки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки.

Величина случайной ошибки репрезентативности зависит от ряда факторов: объема выборки; степени вариации изучаемого признака в генеральной совокупности; принятого способа формирования выборочной совокупности.

Различают среднюю (стандартную) и предельную ошибку выборки. Средняя ошибка выборки характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Предельной ошибкой выборки принято считать максимально возможное расхождение выборочной и генеральной характеристик, т. е. максимум ошибки при заданной вероятности ее появления. Соотношение между пределом ошибки выборки , гарантируемым с некоторой вероятностью Р(t), и средней ошибкой выборки имеет вид: или , где t – коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t). Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характе ристике выборочной совокупности. На практике величина дисперсии признака в генеральной совокупности, как правило, неизвестна, поэтому в формулы ошибки выборки подставляют дисперсию выборочной совокупности.

Выборочная дисперсия несколько меньше генеральной, в математической статистике доказано, что

Если выборочная совокупность большого объема (то есть n достаточно велико), то соотношение приближается к единице и выборочная дисперсия практически совпадает с генеральной.

Выборку считают безусловно большой, если n>100.

Источник

Виды выборочного наблюдения

Статистическое наблюдение может быть сплошным и несплошным.

Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности. Изучение не всех единиц совокупности, а лишь некоторой части, осуществляется с помощью несплошного наблюдения. Самым распространенным видом несплошного статистического наблюдения является выборочное наблюдение.

Выборочное наблюдение – это такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных случайным образом, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.

На практике выборочное наблюдение применяют в тех случаях, когда изучаемая совокупность велика, и обследовать ее всю практически невозможно, или, когда наблюдение связано с порчей качества продукции (определение прочности нити, качества консервов, жирности молока и т.д.). Кроме того, выборочное наблюдение существенно экономит время, финансовые, материально-технические и трудовые ресурсы, и, как следствие, позволяет более детально исследовать отдельные единицы наблюдения. Благодаря этому, выборочное наблюдение находит широкое применение во всех сферах хозяйственной деятельности. Его используют в опросах общественного мнения, в исследованиях покупательского спроса, формирования доходов и структуры расходов населения, контроля качества продукции, контроля норм выработки и т.д.

Совокупность, из которой производится отбор, называется генеральной, а совокупность отобранных единиц – выборочной совокупностью или выборкой.

В статистике по способу отбора различают следующие виды выборок:

1. Собственно-случайная выборка – предполагает отбор единиц из генеральной совокупности посредством жеребьевки или другого подобного способа (например, тиражи выигрышей лотерейных билетов).

2. Механическая выборка – состоит в том, что отбор единиц в выборочную совокупность осуществляется из генеральной совокупности, разбитой на равные группы по нейтральному признаку, так, что из каждой группы в выборку попадает только одна единица.

3. Типическая выборка – используется, когда генеральная совокупность разбита на несколько однотипных групп по признакам, влияющим на изучаемые показатели, и из каждой типической группы производится индивидуальный отбор единиц в выборочную совокупность.

4. Серийная выборка – предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий).

5. Комбинированная выборка.

При этом отбор единиц в выборочную совокупность может осуществляться двумя методами: повторным и бесповторным.

При повторном отборе попавшая в выборку единица подвергается обследованию, а затем возвращается в генеральную совокупность, где наравне с другими единицами участвует в дальнейшей процедуре отбора. На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков. Например, при проведении маркетинговых исследований мы не можем точно оценить, сколько покупателей предпочитает делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение единиц наблюдения по причине как практически неограниченных объемов совокупности, так и возможной повторной регистрации. Например, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.

При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Ошибки выборки

Любое выборочное наблюдение, как бы грамотно оно ни было организовано, всегда связано с определенными ошибками, которые делятся на два класса:

а) ошибки регистрации являются следствием неправильного установления значения наблюдаемого признака или неправильной записи, они характерны для всех видов наблюдения;

б) ошибки репрезентативности обусловлены тем, что выборочная совокупность не может в точности воспроизвести генеральную совокупность. При этом следует различать:

— систематические ошибки репрезентативности – преднамеренные, связанные с нарушением принципов формирования выборочной совокупности. Например, в выборку попали единицы, характеризующиеся большими (меньшими) по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными (заниженными).

— случайные – обусловлены действием случайных факторов.

Статистически можно оценить только случайные ошибки репрезентативности. Для этого с определенной степенью вероятности определяют величину предельной ошибки, с которой результаты выборочного обследования могут быть распространены на всю генеральную совокупность.

В зависимости от исходных данных и способа отбора единиц в выборку, величина предельной ошибки определяется по формулам, приведенным в таблице 5.1.

Метод отбора Вид выборки	Повторный	Бесповторный
для среднего значения	для доли	для среднего значения	для доли
Собственно-случайная и механическая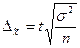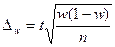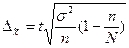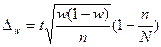
Типическая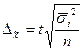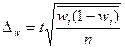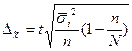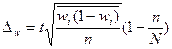
Серийная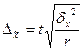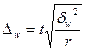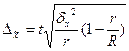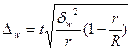

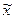
— выборочная средняя;

w – выборочная доля — определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц в выборке n: ;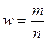

n – число единиц в выборочной совокупности;

N – число единиц в генеральной совокупности;

r – число отобранных серий;

R – общее число серий;

t – величина нормированного отклонения, значение которого соответствует определенному уровню вероятности p

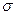
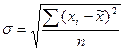
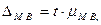
При оценке результатов малой выборки (численность которой не превышает 30 единиц), величина генеральной дисперсии в расчетах не используется. Величина и предельная ошибка малой выборки вычисляются на основе данных выборочного наблюдения:

и ,

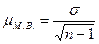
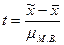
где — мера случайных колебаний выборочной средней в малой выборке, а .

На заключительном этапе на основе предельной ошибки выборки определяют доверительные интервалы, в которых может находиться генеральная средняя или генеральная доля. Выход за пределы этой области имеет весьма малую вероятность. Доверительные интервалы определяются по формулам:

§ для среднего значения: ;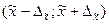

§ для доли: .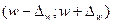

Объем выборки

При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Для этого используют следующие формулы расчета (табл. 5.2).

Вид выборочного наблюдения	Методы отбора
Повторный отбор	Бесповторный отбор
Собственно-случайная и механическая выборка
для среднего значения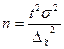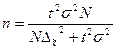
для доли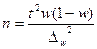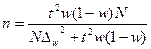
Типическая выборка
для среднего значения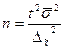
для доли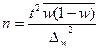
Серийная выборка
для среднего значения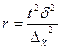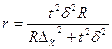
для доли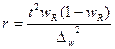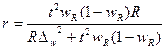

Отметим, что с увеличением предельной ошибки уменьшается необходимый объем выборки, и наоборот.

Дата добавления: 2017-11-04 ; просмотров: 5689 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник