- Раздел 1. Теория статистики
- Оглавление
- 4.1. Особенности выборочного наблюдения. Генеральная и выборочная совокупности
- 4.2. Виды и способы отбора. Виды выборочного наблюдения
- 4.3. Определение ошибки выборочного наблюдения. Средняя и предельная ошибки выборочного наблюдения
- Виды и способы отбора в выборочное наблюдение
- Виды выборки, способы отбора и ошибки выборочного наблюдения
Раздел 1. Теория статистики
Цель: сформировать представление о способах решения задач, которые возникают при использовании выборочного наблюдения.
Задачи: познакомить студентов с методикой различных видов статистического наблюдения, оценки надежности выборочных показателей с учетом их случайной ошибки
Оглавление
4.1. Особенности выборочного наблюдения. Генеральная и выборочная совокупности
Выборочное наблюдение – это вид несплошного наблюдения, которое обеспечивает отбор в случайном порядке части единиц совокупности и возможность последующего распространения полученных данных на всю совокупность единиц.
Исходный массив данных называется генеральной совокупностью. Часть единиц генеральной совокупности, которая непосредственно обследуется при выборочном наблюдении, представляет собой выборочную совокупность. Числовые характеристики генеральной совокупности (средняя, дисперсия и др.) называются параметрами генеральной совокупности.
Организационными вопросами выборочного наблюдения являются: обоснование границ генеральной совокупности; единица отбора; единица наблюдения; способы отбора.
4.2. Виды и способы отбора. Виды выборочного наблюдения
По способу организации различают следующие основные виды выборочного наблюдения: собственно-случайная (простая) выборка; типическая (расслоенная, стратифицированная, районированная); серийная (гнездовая); многоступенчатая; многофазная.
При любом виде выборки отбор единиц производится тремя способами: случайный отбор (жеребьевка, таблица случайных чисел); отбор единиц по какой-либо схеме (единицы упорядочивают таким образом, чтобы это было не связано с изучаемыми свойствами; далее проводится механический отбор единиц); сочетание первого и второго способов.
Простая собственно-случайная выборка проводится из всей массы единиц совокупности без предварительного разделения ее на какие-либо группы. Применяется индивидуальный отбор единиц, т. е. единица отбора совпадает с единицей наблюдения. Типическая, (районированная, стратифицированная) выборка используется в случае, когда генеральная совокупность неоднородна и это влияет на размер изучаемого признака. Серийная выборка (кластерный или гнездовой отбор) – это способ формирования выборки, при котором единица отбора состоит из группы или гнезда более мелких единиц, называемых элементами. Многоступенчатая выборка применяется, когда имеют место несколько стадий отбора (ступеней отбора). При этом каждая стадия имеет свою единицу отбора. Число ступеней отбора определяется числом типов единиц отбора и на последней ступени единица отбора совпадает с единицей выборочной совокупности. Многофазная выборка характеризуется тем, что она также включает несколько ступеней отбора, но на всех ступенях сохраняется одна и та же единица отбора (в отличие от многоступенчатой).
Особым видом выборочного наблюдения является моментное наблюдение – это выборочное во времени наблюдение. Объектом выборки являются отрезки времени. Поэтому понятие генеральной и выборочной совокупности относится не к совокупности единиц, а ко времени наблюдения.
4.3. Определение ошибки выборочного наблюдения. Средняя и предельная ошибки выборочного наблюдения
Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности. Различают систематические и случайные ошибки выборки. Случайные ошибки выборки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки.
Величина случайной ошибки репрезентативности зависит от ряда факторов: объема выборки; степени вариации изучаемого признака в генеральной совокупности; принятого способа формирования выборочной совокупности.
Различают среднюю (стандартную) и предельную ошибку выборки. Средняя ошибка выборки характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Предельной ошибкой выборки принято считать максимально возможное расхождение выборочной и генеральной характеристик, т. е. максимум ошибки при заданной вероятности ее появления. Соотношение между пределом ошибки выборки 



Выборочная дисперсия несколько меньше генеральной, в математической статистике доказано, что
Если выборочная совокупность большого объема (то есть n достаточно велико), то соотношение 
Выборку считают безусловно большой, если n>100.
Источник
Виды и способы отбора в выборочное наблюдение



Точность выборки зависит и от схемы отбора. Различают два вида отбора — повторныйи бесповторный.Первый соответствует схеме «возвращенного шара»: после отбора какой-либо единицы она возвращается в генеральную совокупность и снова может быть выбранной.
При бесповторной выборке отобранная единица не возвращается в генеральную совокупность, поэтому вероятность попадания в выборку для оставшихся единиц увеличивается с каждым шагом отбора.
Деление выборки на повторную и бесповторную введено математической статистикой. В социально-экономических исследованиях повторный отбор применяется очень редко.
По степени охвата единиц исследуемой совокупности различают большиеималые(меньше 30) выборки.
В практике наибольшее распространение получили следующие способы отбора:
1. Собственно-случайный отборили простая выборка (метод жеребьевки, метод лото).
При данном способе отбора каждой единице совокупности присваивается порядковый номер, заносимый на определенные предметы (жетоны, бумажки, фишки, кубики, бочонки, шары или билеты), которые затем перемешиваются и выбираются наугад. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку.
Можно использовать и математические таблицы случайных чисел. Для этого берется любая строка или колонка таблицы, и в выборку включаются указанные номера единиц генеральной совокупности.
На практике чаще применяются схемы бесповторного случайного отбора. Но в торговле выборочное наблюдение может проводиться по схеме повторного отбора. Например, при изучении покупательского спроса населения не исключена повторная регистрация неудовлетворенного спроса одного и того же лица в нескольких магазинах города.
2. Механический отбор.
Механический отбор применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена или ранжирована, то есть имеется определенная последовательность в расположении единиц (списки студентов по алфавиту, телефонные номера абонентов, номера домов, квартир, торговых точек и т.д.). Отбор единиц в выборочную совокупность из генеральной, разбитой на равные интервалы или группы, производится таким образом, что из каждой группы в выборку отбирается лишь одна единица. Например, отбирается каждая первая единица в группе или каждая пятая, десятая, последняя и т.п.
Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков, а используя фактическое размещение единиц генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т. д.
Доказано, что механическая выборка по точности результатов близко подходит к собственно-случайному способу отбора и бывает только бесповторной.
Источник
Виды выборки, способы отбора и ошибки выборочного наблюдения



По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды 
- простая случайная выборка (собственно-случайная);
- типическая (стратифицированная);
- серийная (гнездовая);
- механическая;
- комбинированная;
- ступенчатая.


Для 



Выборочный отбор может быть повторным и бесповторным. При 

Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.
Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки. Для иллюстрации можно предложить расчет ошибки выборки на примере простого случайного отбора.
Расчет средней ошибки повторной простой случайной выборки производится следующим образом:
cредняя ошибка для средней
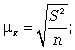
cредняя ошибка для доли
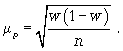
Расчет средней ошибки бесповторной случайной выборки:
средняя ошибка для средней
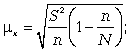
средняя ошибка для доли
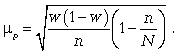
Расчет предельной ошибки 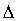
предельная ошибка для средней
предельная ошибка для доли
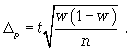
где t — коэффициент кратности;
Расчет предельной ошибки бесповторной случайной выборки:
предельная ошибка для средней
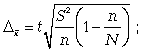
предельная ошибка для доли
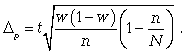
Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N — численность генеральной совокупности.
Что касается расчета ошибки выборки в других видах выборочного отбора (например, типической и серийной), то необходимо отметить следующее.
Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних. Так, в формуле предельной ошибки типической выборки учитывается средняя из групповых дисперсий, т.е.
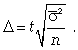
При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии:
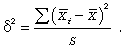
Серийная выборка, как правило, проводится как бесповторная, и формула ошибки выборки в этом случае имеет вид
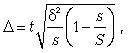
где 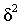
Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n 
При расчете ошибок малой выборки необходимо учесть два момента:
1) формула средней ошибки имеет вид
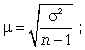
2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности 
В статистических исследованиях с помощью формулы предельной ошибки можно решать ряд задач.
1. Определять возможные пределы нахождения характеристики генеральной совокупности на основе данных выборки.
Доверительные интервалы для генеральной средней можно установить на основе соотношений
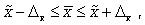
где — 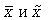
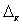
Доверительные интервалы для генеральной доли устанавливаются на основе соотношений
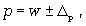
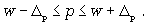
2. Определять доверительную вероятность, которая означает, что характеристика генеральной совокупности отличается от выборочной на заданную величину.
Доверительная вероятность является функцией от t, где
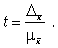
Доверительная вероятность по величине t определяется по специальной таблице.
3. Определять необходимый объем выборки с помощью допустимой величины ошибки:
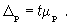
Чтобы рассчитать численность п повторной и бесповторной простой случайной выборки, можно использовать следующие формулы:
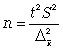
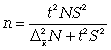
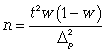
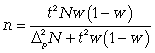
Источник