Виды нестандартных задач способы их решения

Виды нестандартных задач, способы их решения

В данной презентации собраны основые виды нестандартных задач, изучаемых в начальной школе и рассмотрены способы их решения.

Просмотр содержимого документа
«Виды нестандартных задач, способы их решения»

Эффективное решение нестандартных творческих задач

для младших школьников

Знание только тогда знание, когда оно приобретено усилиями твоей мысли, а не памяти.

Развитие творческих способностей – важнейшая задача начального образования, ведь этот процесс пронизывает все этапы развития личности ребёнка, пробуждает инициативу и самостоятельность принимаемых решений, привычку к свободному самовыражению, уверенность в себе.

Творчество – это всегда новое, неизведанное, непредсказуемое, увлекательное и захватывающее.

Одним из средств развития интеллектуальных и творческих способностей младших школьников является решение нестандартных задач.

« Нестандартные задачи – это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения»,- писал Л.М.Фридман.

Нестандартная задача – это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способов решения, ни того, на какой учебный материал опирается решение.

Понятие «нестандартная задача» является относительным.

Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знакомы ли учащиеся со способами решения задач такого типа.

При решении занимательных задач преследуются следующие цели:

• формирование и развитие мыслительных операций: анализа, синтеза, сравнения, аналогии, обобщения и т.д.;
• развитие и тренинг мышления вообще и творческого в частности;
• поддержание интереса к предмету, к учебной деятельности;
• развитие качеств творческой личности (познавательная активность, упорство в достижении цели, самостоятельность, усидчивость);
• подготовка учащихся к творческой деятельности (творческое усвоение знаний, способов действий, умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта)

Помогая ученику, учитель должен оказать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика.

1.Старайся научить своих учеников догадываться.

2.Старайся научить своих учеников доказывать.

3.Пользуйся наводящими указаниями, но не старайся навязывать своего мнения насильно.

Нестандартные задачи по математике, используемые в начальной школе, условно можно разделить на следующие группы :

• задачи на взвешивание
• задачи на переливание;
• задачи, решаемые с «конца»;
• задачи на установление взаимно-однозначного соответствия между множествами;
• задачи о лжецах;
• задачи о переправах;
• задачи, решаемые с помощью логических выводов и т.д.

• алгебраический;
• арифметический;
• графический;
• практический;
• метод предположения;
• метод перебора

• способ рассуждений;
• способ составления таблиц;
• способ построения графов;
• способ бильярда;
• способ кругов Эйлера

Приёмы работы над задачей

1. Изучение условия задачи.

2. Выдвижение идеи(плана) задачи.

3. Поиск аналогии, сравнительные чертежи.

4. Разбиение задачи на подзадачи.

5. Решение одной задачи несколькими способами.

6. Приём разбора готового решения.

Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий :

1. Задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.

2. Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения.

3. Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.

• усвоить процесс решения любой задачи(читаю задачу, выделяю, что известно и что надо узнать);
• познакомиться с приемами работы над задачей(видами наглядной интерпретации, поиска решения, проверки решения задачи и др.)

На втором этапе учащиеся применяют ранее сформулированные общие приемы в ходе самостоятельного поиска решения конкретных задач.

При поиске решения незнакомой задачи полезно сделать чертеж (рисунок), т.к. именно он может быть способом решения задачи.

Если тебе трудно решить задачу, то попробуй:

— сделать к задаче рисунок или чертеж (подумай, может быть нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи);

— ввести вспомогательный элемент (часть);

— использовать для решения задачи способ подбора;

— переформулировать задачу другими словами, чтобы она стала более понятной и знакомой;

— разделить условие или вопрос задачи на части и решить ее по частям;

— начать решение задачи с «конца»

Задачи на взвешивание – достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний.

Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.

Из девяти монет одна фальшивая: она легче остальных.

Как за два взвешивания на чашечных весах без гирь определить, какая именно монета фальшивая?

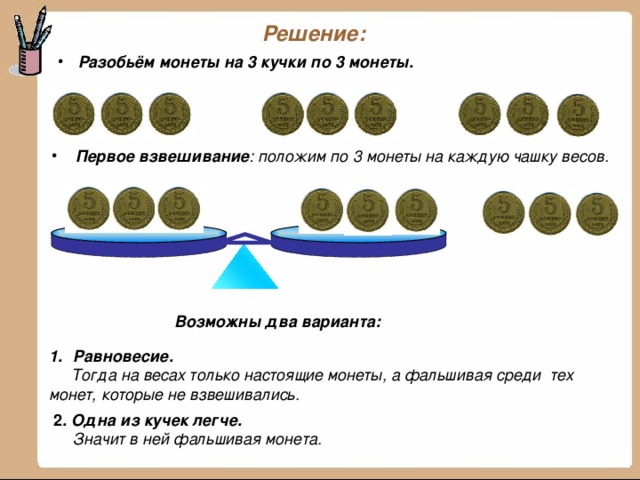
• Разобьём монеты на 3 кучки по 3 монеты.

• Первое взвешивание: положим по 3 монеты на каждую чашку весов.

Возможны два варианта:

Тогда на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались.

Значит в ней фальшивая монета.

• Второе взвешивание:теперь требуется найти фальшивую среди трёх монет ( по методу первого взвешивания).

В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9 кг гвоздей?

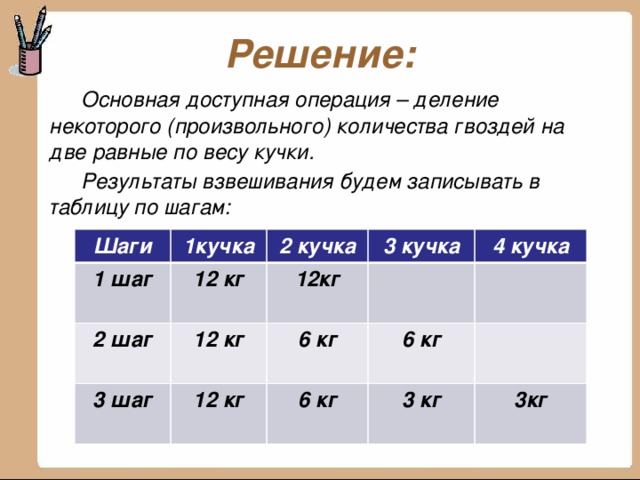
Основная доступная операция – деление некоторого (произвольного) количества гвоздей на две равные по весу кучки.

Результаты взвешивания будем записывать в таблицу по шагам:

Источник

Виды нестандартных задач, способы их решения

В данной презентации собраны основые виды нестандартных задач, изучаемых в начальной школе и рассмотрены способы их решения.

Просмотр содержимого документа
«Виды нестандартных задач, способы их решения»

Эффективное решение нестандартных творческих задач

для младших школьников

Знание только тогда знание, когда оно приобретено усилиями твоей мысли, а не памяти.

Развитие творческих способностей – важнейшая задача начального образования, ведь этот процесс пронизывает все этапы развития личности ребёнка, пробуждает инициативу и самостоятельность принимаемых решений, привычку к свободному самовыражению, уверенность в себе.

Творчество – это всегда новое, неизведанное, непредсказуемое, увлекательное и захватывающее.

Одним из средств развития интеллектуальных и творческих способностей младших школьников является решение нестандартных задач.

« Нестандартные задачи – это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения»,- писал Л.М.Фридман.

Нестандартная задача – это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способов решения, ни того, на какой учебный материал опирается решение.

Понятие «нестандартная задача» является относительным.

Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знакомы ли учащиеся со способами решения задач такого типа.

При решении занимательных задач преследуются следующие цели:

• формирование и развитие мыслительных операций: анализа, синтеза, сравнения, аналогии, обобщения и т.д.;
• развитие и тренинг мышления вообще и творческого в частности;
• поддержание интереса к предмету, к учебной деятельности;
• развитие качеств творческой личности (познавательная активность, упорство в достижении цели, самостоятельность, усидчивость);
• подготовка учащихся к творческой деятельности (творческое усвоение знаний, способов действий, умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта)

Помогая ученику, учитель должен оказать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика.

1.Старайся научить своих учеников догадываться.

2.Старайся научить своих учеников доказывать.

3.Пользуйся наводящими указаниями, но не старайся навязывать своего мнения насильно.

Нестандартные задачи по математике, используемые в начальной школе, условно можно разделить на следующие группы :

• задачи на взвешивание
• задачи на переливание;
• задачи, решаемые с «конца»;
• задачи на установление взаимно-однозначного соответствия между множествами;
• задачи о лжецах;
• задачи о переправах;
• задачи, решаемые с помощью логических выводов и т.д.

• алгебраический;
• арифметический;
• графический;
• практический;
• метод предположения;
• метод перебора

• способ рассуждений;
• способ составления таблиц;
• способ построения графов;
• способ бильярда;
• способ кругов Эйлера

Приёмы работы над задачей

1. Изучение условия задачи.

2. Выдвижение идеи(плана) задачи.

3. Поиск аналогии, сравнительные чертежи.

4. Разбиение задачи на подзадачи.

5. Решение одной задачи несколькими способами.

6. Приём разбора готового решения.

Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий :

1. Задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.

2. Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения.

3. Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.

• усвоить процесс решения любой задачи(читаю задачу, выделяю, что известно и что надо узнать);
• познакомиться с приемами работы над задачей(видами наглядной интерпретации, поиска решения, проверки решения задачи и др.)

На втором этапе учащиеся применяют ранее сформулированные общие приемы в ходе самостоятельного поиска решения конкретных задач.

При поиске решения незнакомой задачи полезно сделать чертеж (рисунок), т.к. именно он может быть способом решения задачи.

Если тебе трудно решить задачу, то попробуй:

— сделать к задаче рисунок или чертеж (подумай, может быть нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи);

— ввести вспомогательный элемент (часть);

— использовать для решения задачи способ подбора;

— переформулировать задачу другими словами, чтобы она стала более понятной и знакомой;

— разделить условие или вопрос задачи на части и решить ее по частям;

— начать решение задачи с «конца»

Задачи на взвешивание – достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний.

Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.

Из девяти монет одна фальшивая: она легче остальных.

Как за два взвешивания на чашечных весах без гирь определить, какая именно монета фальшивая?

• Разобьём монеты на 3 кучки по 3 монеты.

• Первое взвешивание: положим по 3 монеты на каждую чашку весов.

Возможны два варианта:

Тогда на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались.

Значит в ней фальшивая монета.

• Второе взвешивание:теперь требуется найти фальшивую среди трёх монет ( по методу первого взвешивания).

В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9 кг гвоздей?

Основная доступная операция – деление некоторого (произвольного) количества гвоздей на две равные по весу кучки.

Результаты взвешивания будем записывать в таблицу по шагам:

Источник