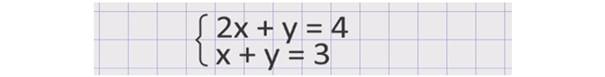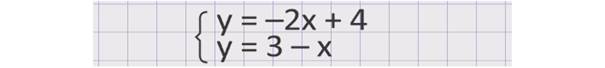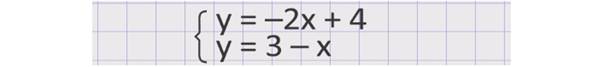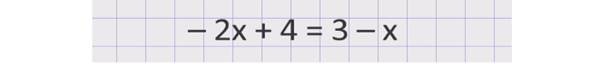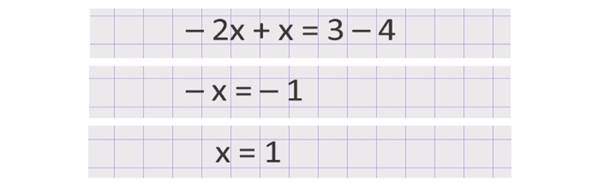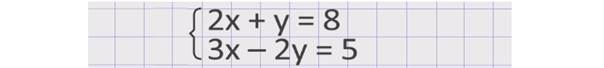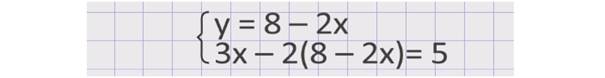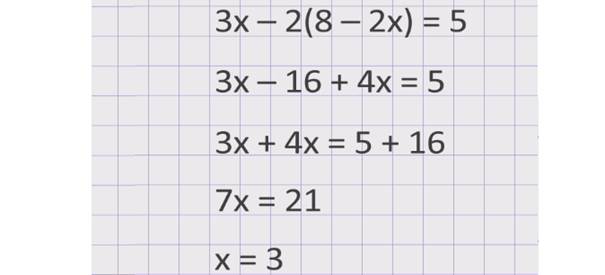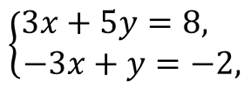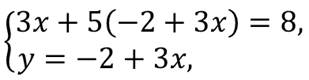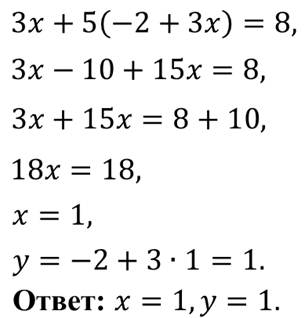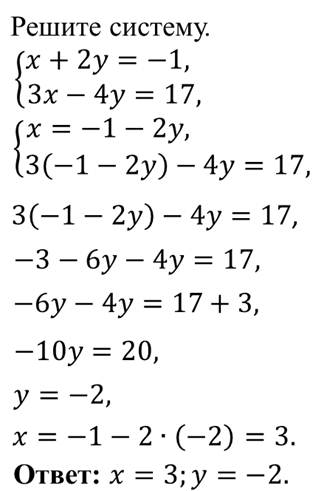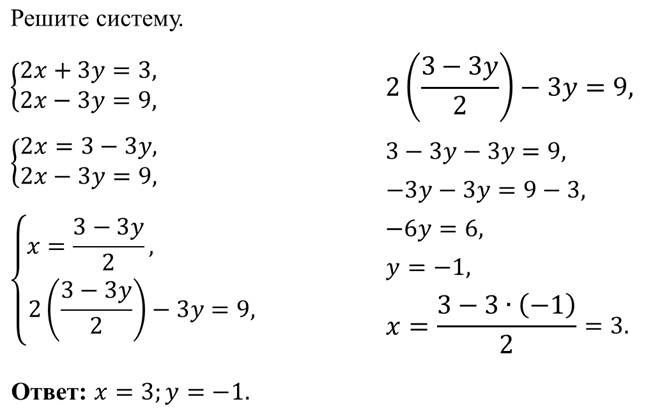Видеоурок системы уравнений способ подстановки

Видеоурок системы уравнений способ подстановки

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

• Главная
• 7-Класс
• Алгебра
• Видеоурок «Решение систем уравнений методом подстановки»

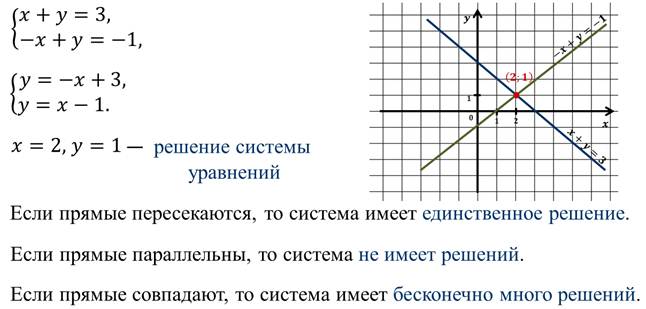
Вспомним, что такое система уравнений.

Система двух уравнений с двумя переменными – это записанные друг под другом два уравнения, объединённые фигурной скобкой. Решить систему – это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.

В этом уроке познакомимся с таким способом решения систем, как способподстановки.

Давайте рассмотрим систему уравнений:

Можно решить эту систему графически. Для этого нам надо будет построить в одной системе координат графики каждого из уравнений, преобразовав их к виду:

Затем найти координаты точки пересечения графиков, которые и будут являться решением системы. Но графический способ далеко не всегда удобен, т.к. отличается малой точностью, а то и вовсе недоступностью. Попробуем рассмотреть нашу систему повнимательнее. Теперь она имеет вид:

Можно заметить, что левые части уравнений равны, а значит, должны быть равны и правые. Тогда мы получим уравнение:

Это знакомое нам уравнение с одной переменной, которое мы решать умеем. Перенесём неизвестные слагаемые в левую часть, а известные – в правую, не забыв поменять знаки +,– при переносе. Получим:

Теперь подставим найденное значение х в любое уравнение системы и найдём значение у. В нашей системе удобнее использовать второе уравнение у = 3 – х, после подстановки получим у = 2. А теперь проанализируем выполненную работу. Сначала мы в первом уравнении выразили переменную у через переменную х. Затем полученное выражение – 2х + 4 подставили во второе уравнение вместо переменной у. Потом решили полученное уравнение с одной переменной х и нашли ее значение. И в заключении использовали найденное значение х для нахождения другой переменной у. Тут возникает вопрос: а обязательно ли было выражать переменную у из обоих уравнений сразу? Конечно нет. Мы могли выразить одну переменную через другую только в одном уравнении системы и использовать его вместо соответствующей переменной во втором. Причём выразить можно любую переменную из любого уравнения. Здесь выбор зависит исключительно из удобства счёта. Подобный порядок действий математики назвали алгоритмом решения систем двух уравнений с двумя переменными методом подстановки.Вот как он выглядит.

1.Выразить одну из переменных через другую в одном из уравнений системы.

2.Подставить полученное выражение вместо соответствующей переменной в другое уравнение системы.

3.Решить полученное уравнение с одной переменной.

4.Найденное значение переменной подставить в выражение, полученное в пункте первом, и найти значение другой переменной.

5.Записать ответ в виде пары чисел, которые были найдены на третьем и четвертом шаге.

Давайте рассмотрим ещё один пример. Решить систему уравнений:

Здесь удобнее выразить переменную у из первого уравнения. Получим у = 8 – 2х. Полученное выражение надо подставить вместо у во второе уравнение. Получим:

Выпишем это уравнение отдельно и решим его. Сначала раскроем скобки. Получим уравнение 3х – 16 + 4х = 5. Соберём неизвестные слагаемые в левой части уравнения, а известные — в правой и приведём подобные слагаемые. Получим уравнение 7х = 21, отсюда х = 3.

Теперь, используя найденное значение х, можно найти:

Ответ: пара чисел (3; 2).

Таким образом, на этом уроке мы научились решать системы уравнений с двумя неизвестными аналитическим, точным способом, не прибегая к сомнительному графическому.

Источник

Решение систем линейных уравнений способом подстановки

Урок 42. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом подстановки»

· показать еще один способ решения систем линейных уравнений – способ подстановки.

На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1. выразить из какого-нибудь уравнения системы одну переменную через другую;

2. подставить вместо этой переменной полученное выражение в другое уравнение системы;

3. решить получившееся уравнение с одной переменной;

4. найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.

Источник

Конспекты уроков по теме; «Решение систем линейных уравнений способом подстановки»

Муниципальное общеобразовательное учреждение

«Чернослободская основная школа»

Шацкий муниципальный район

Конспекты уроков по теме;

«Решение систем линейных уравнений способом подстановки»

Автор: Трандина Л.Н. учитель математики

МОУ «Чернослободская ОШ»

Шацкого района Рязанской области

Тема урока : «Решение систем линейных уравнений способом подстановки»

Сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки.

Вырабатывать умение выражать из какого-нибудь уравнения системы одну переменную через другую.

Развивать умение обобщать, анализировать, логически мыслить.

Воспитывать интерес к предмету через содержание учебного материала.

Оборудование: мультимедийный проектор, доска, мел, карточки.

Актуализация опорных знаний.

1. Является ли пара чисел (2; 3) решением системы уравнений:

а) б) в)

2. Сколько решений имеет система уравнений:

а) б) в)

Вывод: коэффициенты при х различны, то система имеет одно решение;

если коэффициенты при х одинаковы, то система не имеет решений.

3. Выразите у через х: а) х + у = 2; б) у – 6х = 1; в) х – у = 4.

4. Выразите х через у: а) х + у = 6; б) х – 2у = 4; в) 2у – х = 1.

II. Объяснение нового материала.

Объяснение проводится согласно пункту 43 учебника.

1. Рассмотрите пример 1, учебника, что данный способ решения систем уравнений называется способом подстановки.

2. Выучите определение равносильных систем уравнений.

3. Записываем в тетрадях алгоритм решения систем уравнений способом подстановки . При этом каждый шаг алгоритма должен отражаться соответствующим действием в решении системы уравнений.

Выразить из какого-нибудь уравнения системы
одну переменную через другую

Подставить в другое уравнение системы вместо
этой переменной полученное выражение

Решить полученное уравнение с одной
переменной

Найти соответствующее значение второй
переменной

Обращаю ваше внимание , что выражать следует ту переменную, при которой стоит более «удобный» коэффициент (в частности ±1).

III. Формирование умений и навыков.

Желательно, чтобы вы запомнили алгоритм решения систем уравнений способом подстановки и могли его применять, не обращаясь к записям в тетрадях и разобранным примерам.

1. Выразите в уравнениях х через у и у через х .

Проверка а) х + у = 5; х = 5 – у; у= 5 – х .

б) у – х = –2; — х = — у – 2; х = у +2; у= х – 2.

Выразим у через х, подставим во второе уравнение.

а)

Вычислим, соответствующее значение переменной у

в)

– Что называется решением системы уравнений с двумя переменными?

– Какие вы знаете способы решения систем уравнений?

– Сформулируйте алгоритм решения систем уравнений способом подстановки.

– Из какого уравнения системы лучше выражать переменную?

V. На дом : п.43; № 1069(б,г,д,е).

Тема урока : «Решение систем линейных уравнений способом подстановки »

Цели: продолжить формирование умения решать системы уравнений способом подстановки. проверить первоначальный уровень усвоения материала.

Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.

Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.

Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.

Тип урока: урок закрепления знаний

I. Устная работа.

1.Является ли пара чисел (–3; 1) решением системы уравнений:

а)

2. Выразите в уравнении х через у и у через х .

II. Формирование умений и навыков.

На этом уроке мы будем решать системы уравнений, в которых ни один коэффициент при переменных не равен ±1. Сначала нужно разобрать пример 2 из учебника, сделать соответствующие выводы, а затем приступить к выполнению заданий (стр.212-213)

Обращаю ваше внимание , что иногда удобнее выражать переменную вместе с её коэффициентом.

а)

v = ;

2 u = –5 ∙ = –1;

u = .

б) Здесь не получится сделать, как в предыдущей системе, поскольку коэффициенты при переменных не являются кратными.

3 p + 4 ∙ p = 29;

3 · 3 р + 4 · 5 р = 29 · 3;

q = p = ∙ 3 = 5.

в)

u = .

3 v = 14 – 4 ∙ 4 ;

3 v = 14 – 17 = –3 ;

v = –1 .

Ответ : .

г)

2 р = –17,5 + 22 = 4,5;

2. Рата по учебнику : № 1073.

Чтобы найти координаты точки пересечения двух прямых, нужно составить и решить соответствующую систему уравнений.

а)

16 х – 5 (23 – 7 х ) = 38;

16 х – 115 + 35 х = 38;

III. Обучающая самостоятельная раюота.

1. Решите систему уравнений способом подстановки и сделайте проверку.

а) б)

– Что называется решением системы уравнений с двумя переменными?

– Сформулируйте алгоритм решения систем уравнений способом подстановки.

– В каких случаях при решении системы уравнений можно выражать переменную вместе с её коэффициентом?

IV. На дом: п. 43; № 1070(в,г),№ 1071(в),1073(б)

Тема урока: «Решение систем линейных уравнений способом подстановки»

Цели: продолжить формирование умения решать системы уравнений способом подстановки., проверить уровень усвоения материала.

Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными; первичная проверка знаний и умений.

Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.

Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.

Тип урока: урок закрепления знаний.

I. Устная работа. Актуализация знаний.

1. Является ли пара чисел (–2; –2) решением системы уравнений:

а)

2. Из какого уравнения системы и какую переменную выразить «удобнее»? Ответ объясните.

а) б)

II. Формирование умений и навыков.

На этом уроке мы будут решать системы уравнений, в которых до применения алгоритма решения системы уравнений с двумя переменными способом подстановки предварительно необходимо провести ряд тождественных преобразований.

Я думаю, решение таких систем не должно у вас вызывать затруднений.

Необходимо раскрыть скобки, привести подобные слагаемые – и система станет похожей на те которые мы уже решали.

3(х – 5) -1 = 6 – 2х 3х – 15-1=6-2х 3х+2х=22

3( х- у) – 7у = -4, 3х – 3у – 7у= -4, 3х -10у=-4,

3х – 10у =-4; 34,4 – 10у =-4; 13,2 -10у=-4 ; -10у= -13,2-4; -10у=-17,2; у=1,72

Мы уже знаем, что если в линейном уравнении встречаются дроби, то обе части уравнения нужно умножать на наименьший общий знаменатель этих дробей.

Таким же приёмом пользуются и при решении систем уравнений .

а)

Замечание . Обращаем внимание на опечатку: во втором уравнении системы вместо –2 должно стоять –1.

в)

2 (35 п + 120) + 5 п = 15;

70 п + 240 + 5 п = 15;

3 т = 35 · (–3) + 120;

3 т = –105 + 120 = 15;

Первичная проверка знаний и умений ( самостоятельная работа).

1. Решите систему уравнений способом подстановки

а) б)

в )

– Что называется решением системы уравнений с двумя переменными?

– Сформулируйте алгоритм решения системы уравнений способом подстановки.

– Как, не выполняя построений, найти координаты точки пересечения графиков двух уравнений?

– Как следует начать решение системы уравнений, в которой встречаются дробные коэффициенты?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 829 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 296 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 607 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1454538

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Пензенской области запустят проект по снижению административной нагрузки на учителей

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Студентам вузов могут разрешить проходить практику у ИП

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник