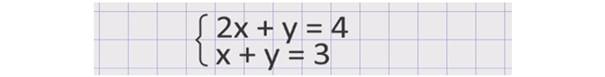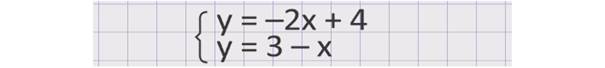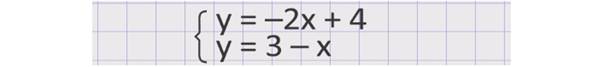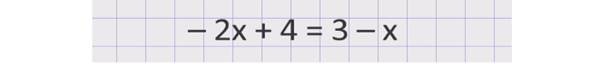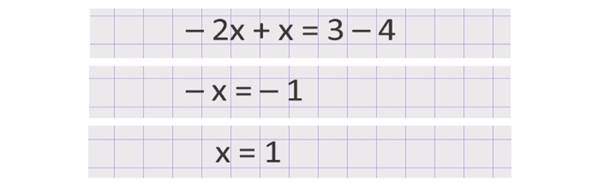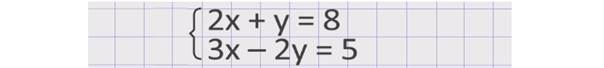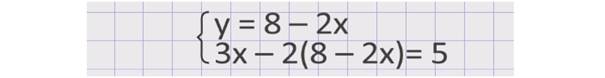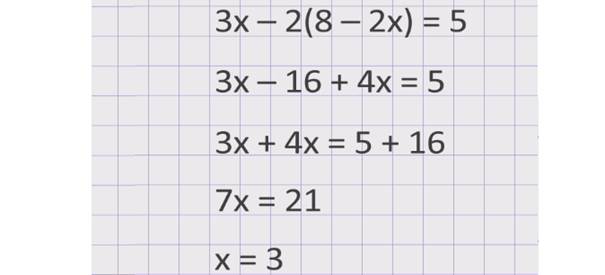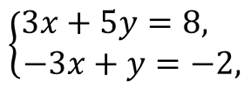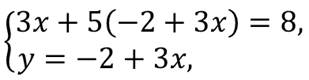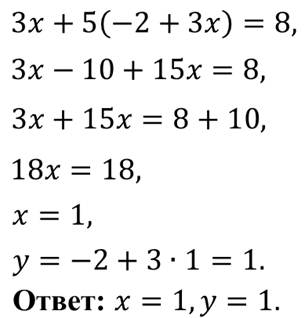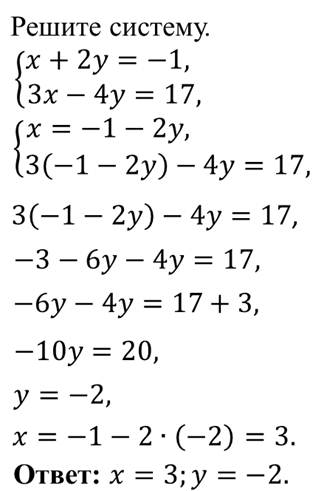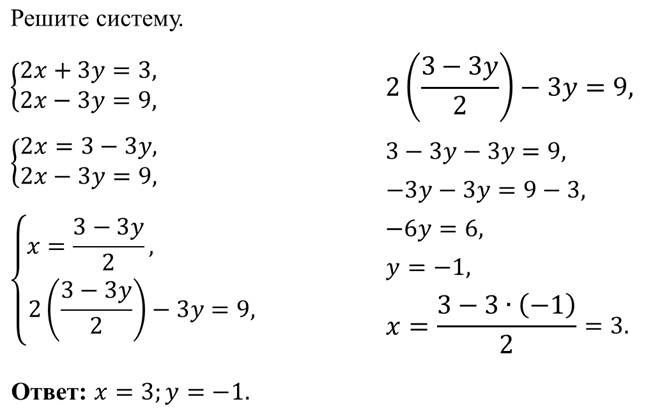Видеоурок решение системы уравнений способом подстановки

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

Главная
7-Класс
Алгебра
Видеоурок «Решение систем уравнений методом подстановки»

Вспомним, что такое система уравнений.

Система двух уравнений с двумя переменными – это записанные друг под другом два уравнения, объединённые фигурной скобкой. Решить систему – это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.

В этом уроке познакомимся с таким способом решения систем, как способподстановки.

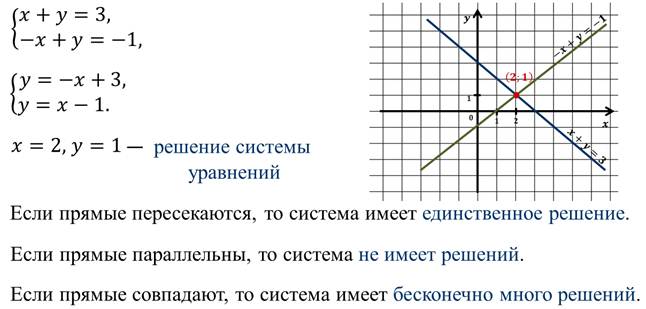
Давайте рассмотрим систему уравнений:

Можно решить эту систему графически. Для этого нам надо будет построить в одной системе координат графики каждого из уравнений, преобразовав их к виду:

Затем найти координаты точки пересечения графиков, которые и будут являться решением системы. Но графический способ далеко не всегда удобен, т.к. отличается малой точностью, а то и вовсе недоступностью. Попробуем рассмотреть нашу систему повнимательнее. Теперь она имеет вид:

Можно заметить, что левые части уравнений равны, а значит, должны быть равны и правые. Тогда мы получим уравнение:

Это знакомое нам уравнение с одной переменной, которое мы решать умеем. Перенесём неизвестные слагаемые в левую часть, а известные – в правую, не забыв поменять знаки +,– при переносе. Получим:

Теперь подставим найденное значение х в любое уравнение системы и найдём значение у. В нашей системе удобнее использовать второе уравнение у = 3 – х, после подстановки получим у = 2. А теперь проанализируем выполненную работу. Сначала мы в первом уравнении выразили переменную у через переменную х. Затем полученное выражение – 2х + 4 подставили во второе уравнение вместо переменной у. Потом решили полученное уравнение с одной переменной х и нашли ее значение. И в заключении использовали найденное значение х для нахождения другой переменной у. Тут возникает вопрос: а обязательно ли было выражать переменную у из обоих уравнений сразу? Конечно нет. Мы могли выразить одну переменную через другую только в одном уравнении системы и использовать его вместо соответствующей переменной во втором. Причём выразить можно любую переменную из любого уравнения. Здесь выбор зависит исключительно из удобства счёта. Подобный порядок действий математики назвали алгоритмом решения систем двух уравнений с двумя переменными методом подстановки.Вот как он выглядит.

1.Выразить одну из переменных через другую в одном из уравнений системы.

2.Подставить полученное выражение вместо соответствующей переменной в другое уравнение системы.

3.Решить полученное уравнение с одной переменной.

4.Найденное значение переменной подставить в выражение, полученное в пункте первом, и найти значение другой переменной.

5.Записать ответ в виде пары чисел, которые были найдены на третьем и четвертом шаге.

Давайте рассмотрим ещё один пример. Решить систему уравнений:

Здесь удобнее выразить переменную у из первого уравнения. Получим у = 8 – 2х. Полученное выражение надо подставить вместо у во второе уравнение. Получим:

Выпишем это уравнение отдельно и решим его. Сначала раскроем скобки. Получим уравнение 3х – 16 + 4х = 5. Соберём неизвестные слагаемые в левой части уравнения, а известные — в правой и приведём подобные слагаемые. Получим уравнение 7х = 21, отсюда х = 3.

Теперь, используя найденное значение х, можно найти:

Ответ: пара чисел (3; 2).

Таким образом, на этом уроке мы научились решать системы уравнений с двумя неизвестными аналитическим, точным способом, не прибегая к сомнительному графическому.

Источник

Решение систем линейных уравнений способом подстановки

Урок 42. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом подстановки»

· показать еще один способ решения систем линейных уравнений – способ подстановки.

На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1. выразить из какого-нибудь уравнения системы одну переменную через другую;

2. подставить вместо этой переменной полученное выражение в другое уравнение системы;

3. решить получившееся уравнение с одной переменной;

4. найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.

Источник

Системы уравнений

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.

Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют « x » и « y »), которые объединены в общую систему фигурной скобкой.

Например, система уравнений может быть задана следующим образом.

x + 5y = 7

3x − 2y = 4

Чтобы решить систему уравнений, нужно найти и « x », и « y ».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

x + 5y = 7

3x − 2y = 4

Выразим из первого уравнения « x + 5y = 7 » неизвестное « x ».

Чтобы выразить неизвестное, нужно выполнить два условия:

перенести неизвестное, которое хотим выразить, в левую часть уравнения;
разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.

Перенесём в первом уравнении « x + 5 y = 7 » всё что содержит « x » в левую часть, а остальное в правую часть по правилу переносу.

При « x » стоит коэффициент равный единице, поэтому дополнительно делить уравнение на число не требуется.

x = 7 − 5y

3x − 2y = 4

Теперь, вместо « x » подставим во второе уравнение полученное выражение
« x = 7 − 5y » из первого уравнения.

x = 7 − 5y

3(7 − 5y) − 2y = 4

Подставив вместо « x » выражение « (7 − 5y) » во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным « y ». Решим его по правилам решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение « 3(7 − 5y) − 2y = 4 » отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*) .

x = 7 − 5y

3(7 − 5y) − 2y = 4 (*)

Мы нашли, что « y = 1 ». Вернемся к первому уравнению « x = 7 − 5y » и вместо « y » подставим в него полученное числовое значение. Таким образом можно найти « x ». Запишем в ответ оба полученных значения.

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.

x + 5y = 7

3x − 2y = 4

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.

x + 5y = 7	(x + 5y) + (3x − 2y) = 7 + 4
+ =>	x + 5y + 3x − 2y = 11
3x − 2y = 4	4x + 3y = 11

При сложении уравнений мы получили уравнение « 4x + 3y = 11 ». По сути, сложение уравнений в исходном виде нам ничего не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

x + 5y = 7

3x − 2y = 4

Чтобы при сложении неизвестное « x » взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при « x » стоял коэффициент « −3 ».

Для этого умножим первое уравнение на « −3 ».

При умножении уравнения на число, на это число умножается каждый член уравнения.

x + 5y = 7 | ·(−3)

3x − 2y = 4

x · (−3) + 5y · (−3) = 7 · (−3)

3x − 2y = 4

−3x −15y = −21

3x − 2y = 4

Теперь сложим уравнения.

−3x −15y = −21	(−3x −15y ) + (3x − 2y) = −21 + 4
+ =>	− 3x − 15y + 3x − 2y = −21 + 4
3x − 2y = 4	−17y = −17 \|:(−17)
y = 1

Мы нашли « y = 1 ». Вернемся к первому уравнению и подставим вместо « y » полученное числовое значение и найдем « x ».

x = 7 − 5y

y = 1

x = 7 − 5 · 1

y = 1

x = 2

y = 1

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения « x ».

x = 17 + 3y

x − 2y = −13

Подставим вместо « x » во второе уравнение полученное выражение.

x = 17 + 3y

(17 + 3y) − 2y = −13 (*)

Подставим в первое уравнение полученное числовое значение « y = −30 » и найдем « x ».

x = 17 + 3y

y = −30

x = 17 + 3 · (−30)

y = −30

x = 17 −90

y = −30

x = −73

y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

3(x − y) + 5x = 2(3x − 2)

4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

3x − 3y + 5x = 6x − 4

4x − 2x − 2y = 4 − 3y

8x − 3y = 6x − 4

2x −2y = 4 − 3y

8x − 3y − 6x = −4

2x −2y + 3y = 4

2x − 3y = −4

2x + y = 4

Мы видим, что в обоих уравнениях есть « 2x ». Наша задача, чтобы при сложении уравнений « 2x » взаимноуничтожились и в полученном уравнении осталось только « y ».

Для этого достаточно умножить первое уравнение на « −1 ».

2x − 3y = −4 | ·(−1)

2x + y = 4

2x · (−1) − 3y · (−1) = −4 · (−1)

2x + y = 4

−2x + 3y = 4

2x + y = 4

Теперь при сложении уравнений у нас останется только « y » в уравнении.

−2x + 3y = 4	(−2x + 3y ) + (2x + y) = 4 + 4
+ =>	− 2x + 3y + 2x + y = 4 + 4
2x + y = 4	4y = 8 \| :4
y = 2

Подставим в первое уравнение полученное числовое значение « y = 2 » и найдем « x ».

Источник

Видеоурок решение системы уравнений способом подстановки