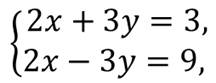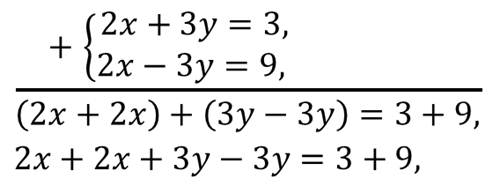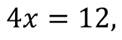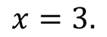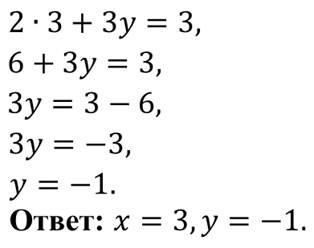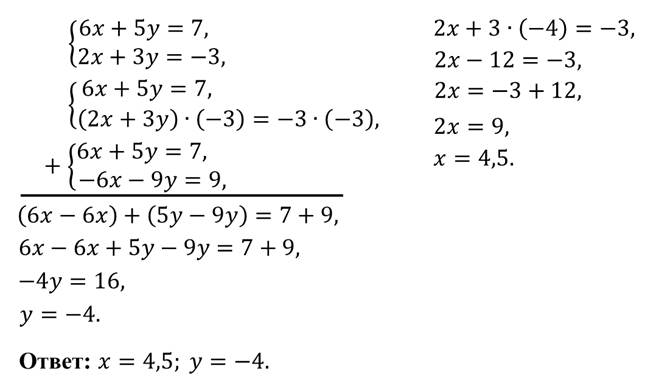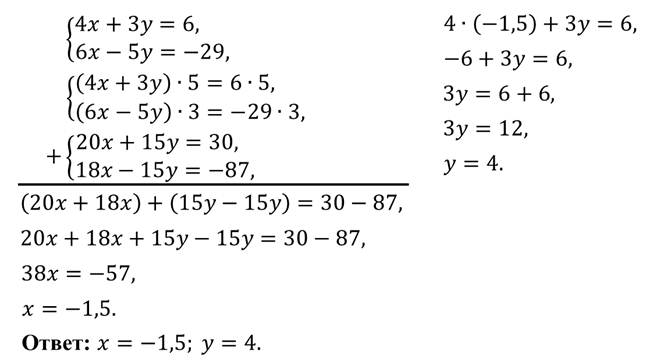Видеоурок решение системы способом сложения

Решение систем линейных уравнений способом сложения

Урок 43. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом сложения»

· показать еще один способ решения систем линейных уравнений – способ сложения.

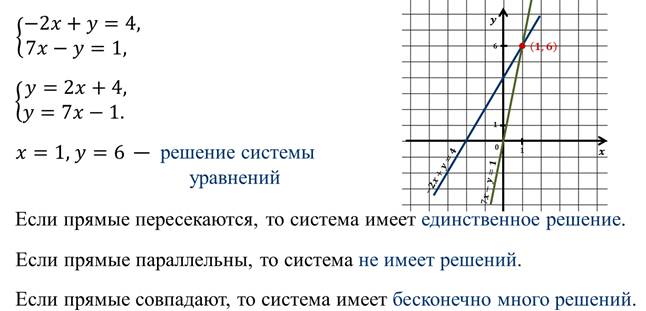
Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.

На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.

Рассмотрим следующую систему

Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений

Приведём подобные слагаемые в обеих частях получившегося уравнения

Видим, что получили уравнение с одной переменной.

Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.

Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.

Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:

1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений системы;

3) решить получившееся уравнение с одной переменной;

4) найти соответствующее значение второй переменной.

При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.

Источник

Решение систем линейных уравнений способом сложения

Урок 43. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом сложения»

· показать еще один способ решения систем линейных уравнений – способ сложения.

Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.

На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.

Рассмотрим следующую систему

Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений

Приведём подобные слагаемые в обеих частях получившегося уравнения

Видим, что получили уравнение с одной переменной.

Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.

Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.

Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:

1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений системы;

3) решить получившееся уравнение с одной переменной;

4) найти соответствующее значение второй переменной.

При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Немного теории.

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 3x+y=7 \\ -5x+2y=3 \end \right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ \left\< \begin y = 7—3x \\ -5x+2(7-3x)=3 \end \right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 2x+3y=-5 \\ x-3y=38 \end \right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ \left\< \begin 3x=33 \\ x-3y=38 \end \right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение \( x-3y=38 \) получим уравнение с переменной y: \( 11-3y=38 \). Решим это уравнение:
\( -3y=27 \Rightarrow y=-9 \)

Таким образом мы нашли решение системмы уравнений способом сложения: \( x=11; y=-9 \) или \( (11; -9) \)

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Источник

Урок «Решение систем уравнений способом сложения «

Выбранный для просмотра документ способ сложения.ppt

Описание презентации по отдельным слайдам:

РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ

МЕТОД РЕШЕНИЯ ХОРОШ, ЕСЛИ МЫ С САМОГО НАЧАЛА МОЖЕМ ПРЕДВИДЕТЬ – И ДАЛЕЕ ПОДТВЕРДИТЬ ЭТО, ЧТО , СЛЕДУЯ ЭТОМУ МЕТОДУ,МЫ ДОСТИГНЕМ ЦЕЛИ. Г.Лейбниц

Горы устных вычислений

Сколько решений может иметь с.л.у.? Одно решение Бесконечно много решений Не имеет решений Прямые совпадают Прямые пересекаются Прямые параллельны

2x-y=6 (…;0) (3;…) (4;…) 3 0 2 Найти неизвестное число в паре, которая является решением уравнения

Проходят ли через точку К(6;3) графики уравнений: а) y=-2x; б) у=-2х+15; в) 2х+у-5=0? а) нет; б) да; в) нет.

Деревня Теоретическая 1)Что называют решением системы уравнений? 2) Что значит решить систему уравнений? 3) Какие методы решения систем уравнений вы знаете? 4) Сформулируйте алгоритм решения системы уравнений методом подстановки.

Поляна систем уравнений

Решить систему уравнений способом сложения х + у = 15, х – у = 1; _______ 2х = 16, Х = 8, 8 + у = 15, у = 15 – 8, у = 7. Ответ: (8; 7)

б) 3х + у = 8,│×2 5х – 2у = 6; ____________ 6х + 2 у = 16, 5х – 2у =6; 11х =22, х = 2. 3×2 + у = 8, 6 + у = 8, у =2. Ответ: (2;2)

Алгоритм способа сложения 1.Умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной переменной стали противоположными числами; 2. Складывают почленно левые и правые части системы; 3. Решают получившееся уравнение с одной переменной; 4. Находят соответствующее значение второй переменной.

Электронная физкультминутка для глаз Prezentacii.com

Остров изученного задания 2а), 3а), 4а из ТПО стр. 95

№ 2 а. Закончите решение системы уравнений. 9х – 10 у = 25, 4х + 5у = 30;│×2 9х – 10у = 25, 8х + 10у = 60;

№ 3 а. Закончите решение системы уравнений. 2х – 5у = 5, │×3 -3х + 4у = -18;│×2 6х – 15у = 15, — 6х + 8у = -36

№ 4 а. Решите систему уравнений способом сложения. 6х – 5у = -12, 4х + 3у = 30;

ЭЙНШТЕЙН (1879-1955г.г.) «Мне приходится распределять свое время между политикой и уравнениями. Но уравнения, полагаю, намного важнее».

Проверочная работа Решите систему уравнений способом сложения 1 вариант а) 2у – х = -8, 4у + х = 2; б) 2х + у = 2, 3х + 4у = 3; 2 вариант а) 3х + у = -3, -5х – у = 7; б) х + 5у = 2, 4х + 7у = -5;

Проверим ответы 1 вариант а) (6; -1) б) (1; 0) 2 вариант а) ( -2; 3) б) (-3; 1)

Посредством уравнений, теорем Я уйму всяких разрешил проблем. Чосер, английский поэт Домашнее задание: алгоритм выучить; №№ 1082 (а,в); 1083 (а,в).

Спасибо за урок !

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-421673

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Российский совет олимпиад школьников намерен усилить требования к олимпиадам

Время чтения: 2 минуты

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Попова предложила изменить школьную программу по биологии

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник