Видеоурок практические способы построения параллельных прямых

Содержание

Урок «Практические способы построения параллельных прямых»
Видеоурок «Параллельные прямые»
Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок
Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок
Урок 45 Бесплатно Параллельные прямые
Параллельные прямые

Урок «Практические способы построения параллельных прямых»

Краткое описание документа:

Видеоурок «Практические способы построения параллельных прямых» содержит информацию о способах построения параллельных прямых, основанных на изученных ранее семиклассниками закономерностях, касающихся параллельных прямых. Задача данного видеоурока – предоставить информацию о способах построения параллельных прямых, формировать умения школьников корректно производить геометрические построения, использовать на практике полученные знания о важных свойствах геометрических фигур.

Данный видеоурок может заменить подачу учебного материала учителем, так как содержит подробно объяснение механизмов построения, обладает высокой степенью наглядности. При помощи анимационных эффектов построения, производимые в ходе видеоурока, приближены к проведению реальных построений на учебной доске. Данный видеоурок освобождает учителя для проведения более эффективной индивидуальной работы с учениками.

Видеоурок начинается с вывода на экран названия темы. В начале видеоурока ученики извещаются о том, что изученные ими признаки параллельности прямых широко применяются на практике, и при решении геометрических задач они нередко столкнуться с необходимостью производить построения, в которых прямо используются данные свойства. Отмечается, что есть несколько способов, используемых для построения параллельных прямых, которые применяются в зависимости от имеющегося набора инструментов для построения.

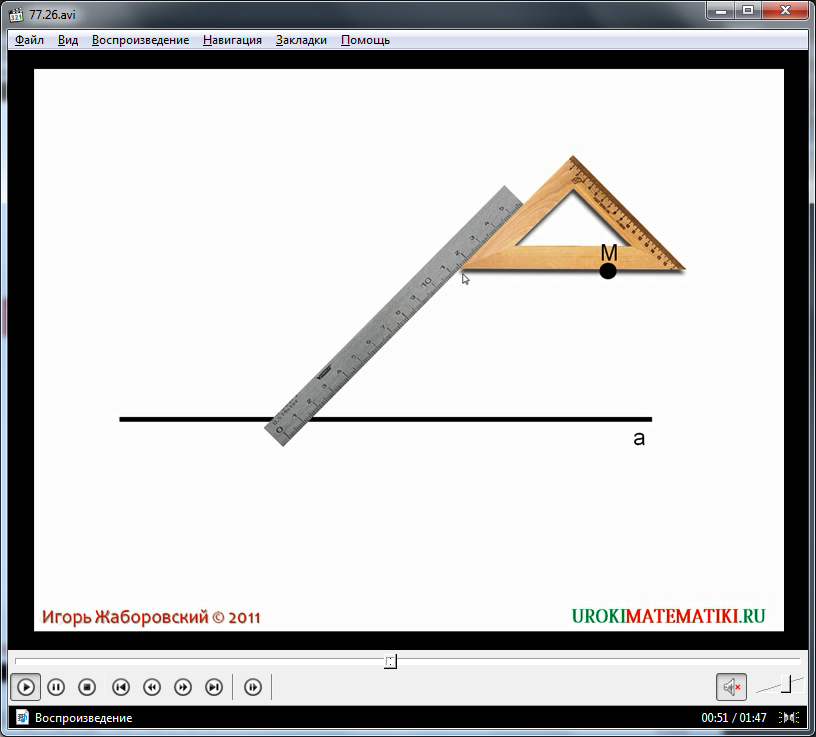
Далее рассматривается построение параллельных прямых, которое выполняется линейкой и чертежным угольником. Условие задачи на построение – есть прямая а и отмеченная вне ее точка М. Необходимо через М провести некоторую прямую, которая будет параллельна а. Чтобы произвести построение, к прямой а прилагается сторона чертежного угольника. К другой стороне угольника прилагается линейка. После передвижения угольника вдоль приложенной линейки можно при помощи используемой ранее стороны провести прямые, которые параллельны первой. Продвинув угольник так, чтобы проводимая прямая проходила через точку М, формируем искомую фигуру – прямую b. Анимированное изображение позволяет наглядно изобразить ход данного построения, продемонстрировать его понятно для учеников. Наглядное построение на видео позволяет заметить, что в данном случае в ходе решения задачи используется признак параллельности прямых, который построен на равенстве соответственных углов, образуемых секущей. На рисунке эти углы отмечены ∠α и ∠β.

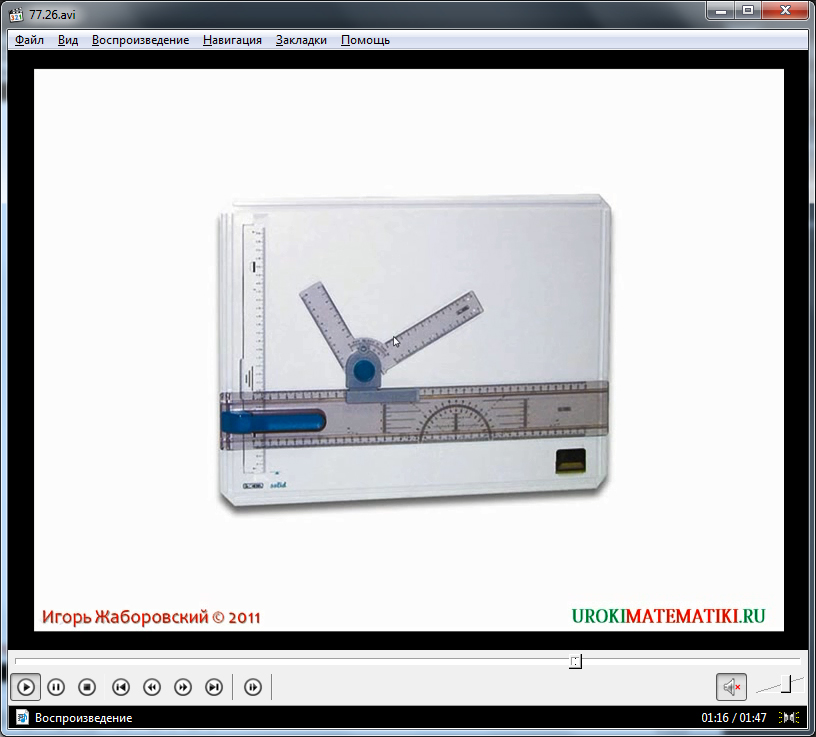
Следующая часть видеоурока посвящена построению параллельных прямых, выполняемому при помощи рейсшины. На рисунке изображена рейсшина, при помощи указателей отмечается передвижение ее части, при помощи которой можно построить параллельные прямые. Отмечается, что данный инструмент широко распространен в практике построения технических чертежей.

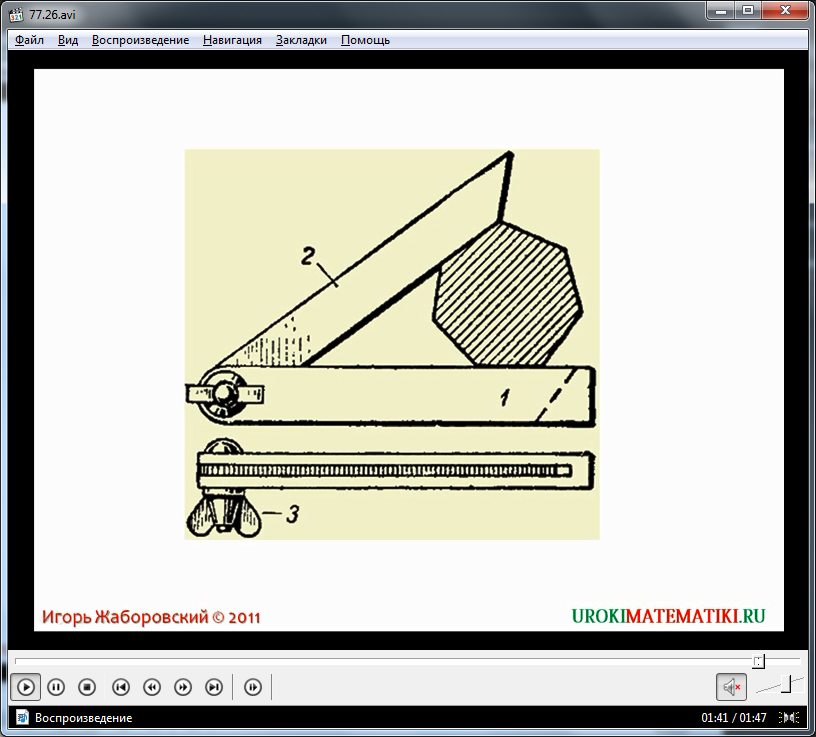
В последней части видеоурока демонстрируется инструмент для построения параллельных прямых, используемый на практике при выполнении столярных работ. Данный инструмент называется малка. Принцип построения при помощи малки аналогичен построению, выполняемому при помощи рейсшины. Он состоит из двух деревянных планок, скрепленных шарниром.

Видеоурок может быть использован учителем в ходе проведения урока по данной теме для наглядной демонстрации изучаемых способов построения и инструментов для выполнения подобных задач. Материал поможет освоить данные способы построения самостоятельно, а также будет полезен при дистанционном обучении геометрии.

Источник

Видеоурок «Параллельные прямые»

Цели урока

Образовательные цели: обобщить и систематизировать знания по теме «Параллельные прямые», реализовать знания и умения по данной теме для решения задач.

Развивающие цели: содействовать развитию памяти, внимания, воображения, правильной математической речи.

Воспитательные цели: воспитать уверенность, целеустремленность, трудолюбие; стимулировать мотивацию и интерес к изучению геометрии.

Тип урока: урок обобщающего повторения по теме «Параллельные прямые».

Ход урока

1. Организационный момент:

─ проверка готовности учащихся к уроку;

─ организация внимания учащихся.

2. Повторение теоретического материала

Начнем урок мы с определения параллельных прямых.

А теперь давайте вспомним признаки параллельности прямых и докажем их.

3. Выполнение практических заданий

Давайте рассмотрим решение некоторых задач по теме «Параллельные прямые».

4. Подведение итогов

На этом уроке мы говорили о параллельных прямых. Вспомнили признаки параллельных прямых и доказали их. А затем рассмотрели решение некоторых задач по теме «Параллельные прямые».

5. Рефлексия

Хотелось бы узнать: понравился ли вам урок? Что было непонятным на уроке? Что еще вы хотели бы узнать?

Источник

Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок

Видеоуроки являются идеальными помощниками при изучении новых тем, закреплении материала, для обычных и факультативных занятий, для групповой и индивидуальной работы. Они содержат оптимальное количество графической и анимационной информации для сосредоточения внимания и удержания интереса ребят без отвлечения от сути занятия. Каждый видеоурок озвучен профессиональным мужским голосом, четким и приятным для восприятия.

Ученики ценят оригинальность подачи материала, родители радуются повышению отметок детей, а учителя в восторге от эффекта и экономии времени и денег при подготовке к урокам.
★Инфоурок★
Крупнейший в России образовательный онлайн-проект

✓ Курсы дополнительного образования детей и взрослых: https://infourok.ru/
✓ Тесты для учителей и воспитателей: https://infourok.ru/tests
✓ Самые массовые международные дистанционные олимпиады: https://infourok.ru/konkurs
✓ Видеоуроки по 14 предметам: https://infourok.ru/videouroki
✓ Каталог репетиторов: https://infourok.ru/tutor/ru
✓ Библиотека методических материалов для учителей: https://infourok.ru/biblioteka

Адрес редакции и издательства: 214011, РФ,
г. Смоленск, ул. Верхне-Сенная, 4.
info@infourok.ru

Видео Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок канала ИНФОУРОК

Источник

Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок

Адрес редакции и издательства: 214011, РФ,
г. Смоленск, ул. Верхне-Сенная, 4.
info@infourok.ru

Видео Практические способы построения параллельных прямых | Геометрия 7-9 класс #29 | Инфоурок канала ИНФОУРОК

Источник

Урок 45 Бесплатно Параллельные прямые

На этом уроке разберем один из случаев взаимного расположения прямых на плоскости, узнаем, какие прямые называют параллельными.

Дадим представление об основных свойствах и признаках параллельных прямых.

Рассмотрим, с помощью каких инструментов и какими способами можно построить их на плоскости.

Убедимся на примерах в том, что знания о параллельных прямых используются во многих областях нашей жизни.

Параллельные прямые

Из всех известных нам линий самой простой на первый взгляд является прямая линия.

Прямая линия бесконечна, то есть не имеет начала и конца.

Следовательно, изобразить на плоскости мы можем только часть прямой, а общий вид ее мы можем только представить.

Прямую обозначают любой строчной латинской буквой и читают как «прямая а». Но прямая может быть обозначена двумя прописными латинскими буквами, которые располагаются на разных концах прямой, и читают её как «прямая АВ».

Если на прямой отметить точку, то в результате получатся два луча, направленные в разные стороны (как вам уже известно, луч — это часть прямой, ограниченной с одной стороны).

Если на прямой обозначить две точки, то между этими точками образуется отрезок (отрезок — это часть прямой, ограниченной с обоих сторон).

Прямая линия имеет такие характерные особенности:

Через две произвольные точки можно провести прямую и притом только одну.

Через произвольную точку можно провести бесконечное множество прямых.

Две не совпадающие прямые на плоскости или пересекаются, или не пересекаются.

Прямые, лежащие в одной плоскости и непересекающиеся на всем своем протяжении, называются параллельными прямыми.

У меня есть дополнительная информация к этой части урока!

Слово «параллельность» («параллелос») с греческого языка переводится как «идущие рядом».

Термин «параллельность» использовали еще за долго до того, как параллельные прямые приобрели свое определение.

В древности знак для обозначения параллельных прямых имел вид знака, известного нам сегодня, как знак равенства «=».

Например, параллельность прямых а и d записывали так: «а = d».

Но в 1557 году Роберт Рекорд для обозначения равенства ввел знак «равно» в том виде, в котором он сегодня известен нам «=».

Чтобы избежать недоразумений и путаницы, символ параллельности был перевернут вертикально, его стали обозначать «||»

Сейчас параллельность прямых а и d записывают так: «а||d».

Принято считать, что между параллельными прямыми угол равен нулю.

Отрезки, лежащие на параллельных прямых, называются параллельными друг другу.

Отрезки AB и CD параллельны (AB||CD).

Отрезки OM и CD не являются параллельными.

Лучи, лежащие на параллельных прямых, называются параллельными друг другу.

Луч а и b параллельны (а||b).

Аналогично определяется параллельность отрезка и прямой, отрезка и луча, луча и прямой.

Необходимо понимать, что нельзя считать отрезки и лучи параллельными друг другу только за то, что они не пересекаются.

Приведем пример непересекающихся отрезков и лучей, которые вовсе не параллельны друг другу.

Как мы можем заметить, отрезок АВ не пересекает луч (а), но он и не параллелен ему.

Таким образом, отрезки и лучи, лежащие на одной прямой или на параллельных прямых, будут являться параллельными друг другу и этим прямым.

Выясним некоторые признаки и свойства параллельных прямых.

Рассмотрим аксиому параллельности прямых:

(Аксиома — это истинное утверждение, которое не требует доказательств, его принимают как необходимое допущение.)

Через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной.

Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой прямой, параллельной данной.

Таким образом, расстояние между параллельными прямыми везде одинаково, а длина отрезка перпендикуляра, заключенного между двумя параллельными прямыми, есть расстояние между ними.

Подобную ситуацию можно представить, вспомнив железнодорожный путь (рельсы и шпалы) или шведскую лестницу.

Рассмотрим некоторые признаки параллельных прямых:

1. Если две прямые параллельны третьей прямой, то они между собой параллельны

Если а||с и b||с, то а||b.

2. Если две прямые перпендикулярны третьей, то эти две прямые параллельны друг другу.

Если а⊥с и b⊥с, то а||b.

Перейдем к знакомству со свойствами параллельных прямых.

Свойство — это утверждения обратные признакам.

1. Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и ко второй.

Если c||b и а⊥с, то а⊥b.

2. Если несколько параллельных прямых пересечь прямой, то эта прямая пересечет каждую из параллельных прямых, причем под одним и тем же углом.

∠1 = ∠2 = ∠3

Части параллельных прямых, замкнутые между другими параллельными прямыми, равны.

Если а||b и d||c, а⊥с, b⊥c, b⊥d, a⊥d, то отрезки AB = CD и AC = BD.

Верно и обратное утверждение, если противоположные части четырех пересекающихся прямых равны, то эти части параллельны.

Подобную ситуацию можно представить, вспомнив четырехугольную столешницу или табурет.

Существуют другие признаки и свойства параллельных прямых, но они будут рассмотрены вами позже.

У меня есть дополнительная информация к этой части урока!

Параллельность прямых — вопрос, который имеет большую историю.

Главный труд древнегреческого математика Евклида «Начала» (300 лет до н.э.) является первым дошедшим до наших дней теоретическим трактатом по математике, он содержит основы античной геометрии и математики.

В «Началах» Евклид обобщил все ранее известные достижения древнегреческой математики и создал основу для ее дальнейшего изучения и развития.

Главное научное и историческое значение данной работы Евклида заключается в попытках построения теории геометрии на основе аксиом и логических рассуждений.

Изложение материала ведется от общего к частному: определения и аксиомы, далее постулаты, затем задачи и теоремы.

Евклид делает понятия аксиома и постулат различными, но это различие неясно.

Особый интерес и внимание у математиков всех времен и народов вызывала пятая аксиома о параллельных прямых, описанная в первой из тринадцати книг «Начала».

Пятый постулат Евклида о параллельных прямых, в отличие от остальных простых и элементарных для понимания постулатов, казался громоздким и, на первый взгляд, не очень очевидным.

В связи с этим многие математики пытались доказать недоказуемое и вывести постулат из разряда аксиом и представить как теорему.

Любые доказательства сводились к появлению только лишь более простых формулировок постулата.

За два тысячелетия было огромное множество попыток доказать пятый постулат, но каждая из них содержала утверждение, которое невозможно было доказать без использования того самого постулата.

Научные труды «Начала» оказали заметное влияние на развитие теории математики вплоть до наших дней.

Книга была переведена на множество языков.

В современных источниках приводится другая формулировка постулата о параллельных прямых, которая равносильна постулату Евклида.

Принадлежит она Птолемею Проклу: «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной»

Существуют и другие эквивалентные формулировки.

Пройти тест и получить оценку можно после входа или регистрации

Источник