Геодезия
Для студентов аспирантов и преподавателей
Разделы
- Сила тяжести и уровенные поверхности земли
- Геоид и квазигеоид
- Общий земной эллипсоид
- Нормальная земля и фигура реальной земли
- Референц-эллипсоид Красовского
- Координаты и азимуты
- Уклонения отвесных линий
- Азимуты лапласа
- Понятие о редукционной задаче
- Геодезические сети и их назначение
- Основной принцип построения геодезической сети
- Плотность пунктов государственной
- Необходимая точность построения ггс
- Основные методы создания ггс
- Сведения о других методах создания ггс
- Опорные геодезические сети в дореволюционной России
- Схема и программа Ф.Н. Красовского построение государственной триангуляции
- Государственная геодезическая сеть в СССР
- Последовательность выполнения основных геодезических работ
- Пути cовершенствования ггс
- Общие сведения о проектировании ггс
- Рекогносцировка геодезических пунктов
- Расчет высоты геодезических знаков
- Геодезические знаки
- Центры геодезических пунктов
- Априорная оценка точности геодезических сетей
- Определение веса измеряемых величин
- Вычисление обратного веса уравненных элементов
- Априорная оценка точности ггс с моделированием результатов измерений на компьютере
- Оценка точности триангуляции
- Оценка точности рядов и сетей трилатерации по приблеженным формулам
- Оценка точности звеньев полигонометрии
- Согласование точности измерения горизонтальных направлений, азимутов и длин сторон в геодезических сетях
- Условия эксплуатации высокоточных теодолитов
- Общие сведения о высокоточных теодолитах
- Геометрическая схема высокоточного теодолита
- Осевые системы и уровни теодолита
- Лимб высокоточного оптического теодолита
- Зрительные трубы высокоточных теодолитов
- Отсчетное устройство оптического теодолита
- Принцип совмещенного отсчета
- Поверки и исследования высокоточных теодолитов
- Определение рена оптического микрометра
- Погрешности шкалы оптического микрометра
- Определение эксцентриситета алидады и лимба
- Отдельное спасибо
- return_links(2); ?>
Определение веса измеряемых величин
Достоверность и точность уравненных элементов геодезической сети во многом зависит от правильности установления реального веса каждой измеряемой величины. В общем случае вес каждой непосредственно измеренной величины должен вычисляться по формуле
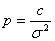
где с — постоянная для сети безразмерная величина (c=const), устанавливаемая до некоторой степени произвольно; 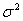
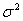
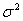
На стадии проектирования средние квадратические ошибки т измеряемых величин задают с учетом имеющегося опыта измерений таких величин в ранее построенных геодезических сетях. В этом случае вес запланированных к измерению в проектируемой сети горизонтальных направлений N, азимутов а, расстояний s вычисляют по формулам
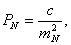
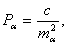
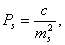
Горизонтальные направления на пунктах геодезической сети каждого данного класса измеряются равноточно. Поэтому целесообразно принять с=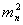
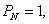
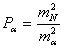
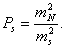
Средние квадратические ошибки измеренных направлений, азимутов, длин сторон можно найти разными способами и получить соответственно разные значения ошибки для одной и той же величины. Например, ошибку измеренного угла в триангуляции можно найти из уравнивания угловых измерений на станции (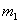
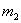
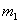
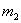
Известно, что совокупное влияние случайных и систематических ошибок на результаты измерений однородных величин наиболее полно сказывается на величинах свободных членов условных уравнений. Поэтому, чтобы получить средние квадратические ошибки, характеризующие реальную точность измерений, следует использовать невязки (свободные члены) условных уравнений.
В триангуляции среднюю квадратическую ошибку измеренного угла вычисляют по невязкам треугольников, используя формулу Ферреро
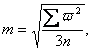
где п — число невязок со треугольников;
средняя квадратическая ошибка измеренного направления равна
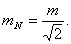
Для определения 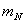
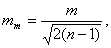
где п — число измерений, т. е. невязок треугольников в данном случае.
При свето- и радиодальномерных измерениях расстояний среднюю квадратическую ошибку 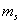
где а0 и а1 — эмпирические коэффициенты. Они указываются в паспорте прибора, а определяются из обработки измерений расстояний разной длины на эталонном полигоне. Однако практика показывает, что реальная точность измерений расстояний далека от величины, получаемой по формуле (5.9).
Наиболее достоверное значение средней квадратической ошибки измерения расстояний в сетях трилатерации и в линейно-угловых сетях можно вычислить по свободным членам со условных уравнений центральных систем и геодезических четырехугольников с измеренными в них длинами сторон:
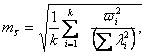
где 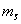
средней длины 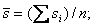
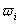
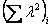
Если известны 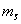
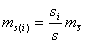
Формулы (5.10) и (5.11) дают несравненно более точные результаты, чем формула (5.9), поэтому их следует применять при вычислении по формулам (5.4) или (5.5) веса измеренных сторон.
Среднюю квадратическую ошибку определения астрономических азимутов на пунктах Лапласа вычисляют обычно по отклонениям значений азимута в приемах от его среднего значения. Величина полученной таким образом ошибки 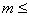
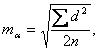
где п — число разностей d; в среднем тa =1,0″, что достаточно хорошо согласуется с другими оценками, полученными, например, при уравнивании обширных блоков астрономо-геодезической сети ( тa 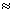
Вопросы надежной оценки точности измерений каждой базисной стороны и каждого азимута на пунктах Лапласа (не по сходимости результатов измерений в приемах) нуждаются в дальнейшем изучении и решении.
Источник
Неравноточные измерения. Вес измерений
Если измерения выполнялись не в одинаковых условиях, то результаты нельзя считать одинаково надежными. Такие измерения называют неравноточными. Например, один и тот же угол можно измерить точным и техническим теодолитом. Результаты данных измерений будут неравноточными.
Мерой сравнения результатов при неравноточных измерениях, т.е. мерой относительной ценности полученных неравноточных результатов является вес результата измерения.
Вес выражает как бы степень доверия, оказываемого данному результату по сравнению с другими результатами.
Чем надежнее результат, тем больше его вес.
Вес измерения – это отвлеченное число, обратно пропорциональное квадрату СКП (среднеквадратическая погрешность)результата измерения.
P = К / m2,
где P – вес результата измерения,
К – произвольное постоянное число для данного ряда измерений,
m – СКП (среднеквадратическая погрешность)результата измерения.
Из формулы видно, что чем меньше СКП измерения, тем оно точнее и его вес больше.
Отношение весов двух измерений обратно пропорционально квадратам СКП этих измерений, т.е.:
P1 / P2 = m22 / m12
Если имеется ряд измерений l1, l2, …, ln, то очевидно, что вес одного измерения будет меньше веса среднего арифметического этих значений, т.е.:
A0 = (a1P1 + a2P2 + … + anPn) / (P1 + P2 + … +Pn),
где A0 – общая арифметическая середина,
ai – результат отдельно взятого измерения,
Pi – вес отдельно взятого измерения.
СКП любого результата измерения равна погрешности измерения с весом 1, делимой на корень квадратный из веса этого результата, т.е.:
где m – СКП любого результата измерения;
M – погрешность измерения с весом 1;
P – вес данного результата измерения.
СКП (среднеквадратическая погрешность) измерения с весом 1 равна корню квадратному из дроби, в числителе которой – сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
где ∆ — абсолютная погрешность неравноточного измерения;
n – число измерений.
Геодезические сети.
Геодезической сетью называют систему закрепленных на местности точек земной поверхности, положение которых определено в общей для них системе координат и высот. Точки, относящиеся к геодезической сети называют геодезическими пунктами.
Геодезические сети могут создаваться как на малых, так и на огромных площадях земной поверхности. По территориальному признаку их можно подразделить на глобальную (общеземную) геодезическую сеть, покрывающую весь земной шар; национальные (государственные) геодезические сети, создаваемые в пределах территории каждой отдельной страны в единой системе координат и высот, принятой в данной стране; сети сгущения, предназначенные для создания съемочного обоснования топографических съемок; местные геодезические сети, т. е. сети на локальных участках, используемые для решения различных задач в местной системе координат.
Геодезические сети подразделяются на плановые и высотные. Плановые сети служат для определения плановых координат геодезических пунктах Х и Y. Высотные для определения высот пунктов H. Геодезические пункты закреплены на местности по разному, временными и постоянными значками.
Виды геодезических сетей:
1) Государственные геодезические сети- главные сети, имеют большую протяжённость ими покрыта вся территория страны. Предназначены: являются основой для построения низших сетей, для решения научных задач.
2) Сети сгущения: предназначены для увеличения плотности пунктов на 1 площади.
3) Сети съёмочного обоснования на основе которых непосредственно производятся съёмки контуров и рельефа местности, инженерно-геодезические работы при строительстве сооружений.
4) Специальные сети, развиваемые при строительстве сооружений, представляющих к геодезическим работам специальные требования.
Плановые геодезические сети
Плановые сети служат для определения плановых координат геодезических пунктах Х и Y. Представляют собой совокупность пунктов, которые имеют исключительно горизонтальные координаты. Выполняются на плоскости, не требующей дополнительного нивелирования контрольных точек. Используются для составления кадастрового плана земельного участка и межевания территории.
Плановые геодезические сети подразделяются на три категории:
— государственные геодезические сети (ГГС),
— сети сгущения (СС),
— сети съёмочного обоснования (ССО).
Государственные геодезические сети и сети сгущения могут создаваться методами:
триангуляции (построение на местности примыкающих друг к другу треугольников, в которых измеряются все горизонтальные углы и длины сторон треугольника),
полигонометрии (построение на местности системы ломаных линий, называемых полигонометрическими ходами, которые в отдельных случаях замыкаются, образуя многоугольники, называемые полигонами),
трилатирации (линейной триангуляции) — создание геодезических сетей из треугольников, в вершинах которых размещены геодезические пункты с измерением горизонтальных проекций длин всех сторон.
Построение геодезических сетей производится по принципу «от общего к частному», от более крупных и точных построений к более мелким и менее точным.
Государственные геодезические сети по точности и назначению разделяются на четыре класса 1, 2, 3, 4 классы.
Источник




