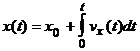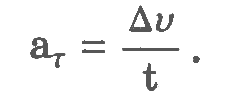Векторный способ описания движения частицы

Механика. Молекулярная физика

Главная > Конспект >Физика

Механика. Молекулярная физика.

Основные понятия и величины

Классическая механика изучает механическое движение частиц (материальных точек) и тел, т.е. изменение положения их в пространстве с течением времени.

Частица (материальная точка) — это тело, размерами которого в условиях

данной задачи можно пренебречь. Одно и то же тело в различных условиях либо может считаться частицей, либо — нет.

Другая абстракция — абсолютно твердое тело — это система частиц,

расстояния между которыми в процессе движения тела остаются неизменными.

При этом постулируется, что:

1) пространство является бесконечным, однородным, изотропным;

2) время является однородным, течет только в одном направлении, а ход времени не зависит от состояния движения тел.

Механическое движение тел рассматривается в системе отсчета .

Кинематика — это раздел механики, рассматривающий движение тел вне

зависимости от причин, вызывающих это движение.

2. Кинематика частицы. Перемещение, скорость, ускорение

Существуют различные способы определения положения частицы.

1) Векторный способ описания движения.

В этом случае положение частицы задается её радиус-вектором . Геометрическое место концов радиус-вектора представляет кривую,

Зависимость радиус-вектора частицы от времени

называется кинематическим уравнением движения . С геометрической

точки зрения — это уравнение траектории.

Изменение радиус-вектора за время ∆t называется перемещением : . Длина дуги траектории между этими точками ∆l назывется путем .

Важнейшей кинематической характеристикой движения является скорость .

Скоростью частицы называется векторная величина, определяемая

иначе говоря, скорость — это производная от радиус-вектора по времени .

Из определения следует, что скорость направлена по касательной

к траектории. Величина скорости

где l — путь, пройденный вдоль траектории.

Иногда используется понятие средней скорости : это векторная

величина, равная отношению перемещения ко времени, т.е.

Скорость изменения скорости частицы по времени, т.е. вектор

называется ускорением частицы.

Таким образом, зная кинематический закон движения, можно простым

дифференцированием по времени найти скорость и ускорение в любой

момент времени (так называемая прямая задача кинематики).

Наоборот, зная ускорение частицы, а также начальные условия ,

т.е. положение и скорость частицы в начальный момент времени,

можно найти траекторию движения частицы (обратная задача

2) Координатный способ описания движения.

Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение частицы в любой момент времени определяется тремя ее координатами x,y,z.Проектируя радиус-вектор на координатные оси, получим три зависимости координат частицы от времени

которые представляют кинематический закон движения в координатной форме.

Модули скорости и ускорения будут

3 ) Естественный способ описания движения. Тангенциальное и

Он обычно используется, если известна траектория движения точки.

При этом начало отсчета

берется на траектории, также выбирается положительное направление

движения вдоль траектории, а положение частицы описывается криволинейной

координатой l(t), представляющей длину дуги кривой линии, отсчитанной вдоль траектории от начальной точки O — иначе говоря, путь . В этом случае l = l(t) — кинематическое уравнение движения.

Свяжем с траекторией естественную систему координат, состоящую из трех взаимно-перпендикулярных осей: касательной (единичный вектор ), нормали (единичный вектор ) и бинормали (единичный вектор ), составляющей правый винт с касательной и нормалью.

Тогда .Ускорение частицы .

Первое слагаемое направлено по касательной к траектории и называется тангенциальным (касательным) ускорением : . Модуль его равен производной от величины скорости по времени, поэтому тангенциальное ускорение характеризует изменение скорости по величине. Второе слагаемое в формуле направлено по нормали к траектории, характеризует изменение скорости по направлению, называется нормальным ускорением и определяется

выражением: . Его модуль . Заметим, что в случае движения частицы по окружности — это хорошо известное центростремительное ускорение .

Итак, полное ускорение можно разложить на две составляющие:

тангенциальное ускорение и нормальное ускорение : , причем модуль полного ускорения .

3. Кинематика вращательного движения твердого тела

Поступательным движением называется такое движение, при котором

все точки тела движутся по одинаковым траекториям, или иначе, любая прямая, связанная с телом, перемещается параллельно самой себе.

При вращении вокруг закрепленной оси все точки движутся по соосным

окружностям. За время dt происходит поворот тела на угол d. Поэтому вместо линейных характеристик вводятся угловые характеристики. Поворот тела на бесконечно малый угол d характеризуется вектором угла поворота , направленным по оси вращения по правилу правого винта.

Элементарный угол поворота является аксиальным вектором.

Быстрота изменения угла поворота характеризуется вектором угловой скорости

направленным так же, как и вектор , т.е. по оси вращения по правилу правого винта.

Еще одна угловая величина — угловое ускорение

Вектор углового ускорения совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном вращении.

Размерности угловых величин: .

Так же, как и при поступательном движении, при вращательном существуют прямая и обратная задачи кинематики.

Прямая задача: по заданному как функция времени углу поворота =(t) найти  z и  z ; решается она дифференцированием по времени:

Обратная задача: по заданному как функция времени угловому ускорению и начальным условиям и найти кинематический закон вращения; она решается с помощью интегрирования:

Динамика. Законы Ньютона и их следствия

1. Сила, масса, импульс

Если кинематика отвечает на вопрос «как происходит движение ?», то

динамика изучает «почему движение происходит именно так ?». Поэтому динамика имеет дело с такими понятиями как сила, масса, импульс и т.п.

Все тела взаимодействуют друг с другом. Количественную меру такого взаимодействия называют силой . Существует множество видов сил, и каждый вид описывается своим силовым законом .

Все тела обладают свойством инертности — свойством противиться

попыткам изменить их движение. Количественная характеристика (мера) такого свойства называется массой (точнее, инертной массой ).

Именно она входит во второй закон Ньютона: .

Совсем другая масса — гравитационная — входит в закон тяготения:

. Но все опыты, проведенные на сегодняшний день, показывают, что эти массы равны:

поэтому в дальнейшем используется один параметр — просто масса .

И, наконец, еще одна динамическая величина — импульс частицы, равный произведению массы частицы на ее скорость :

Импульс — величина векторная.

2. Первый закон Ньютона

Первый закон Ньютона постулирует существование особого класса систем отсчета. Современная формулировка первого закона Ньютона:

существуют такие системы отсчета, в которых свободная частица

движется неускоренно (т.е. равномерно и прямолинейно) . Такие системы отсчета называются инерциальными, а движение свободной частицы в них – движением по инерции. В формулировке закона используется понятие «свободной частицы», которое означает, что на частицу не действуют никакие силы.

Если инерциальная система отсчета найдена, то любая другая, движущаяся относительно нее неускоренно, тоже будет инерциальной. Поэтому можно говорить о бесконечном множестве ИСО.

3. Преобразования координат Галилея

Рассмотрим две системы отсчета: инерциальную систему K и систему К`,

движущуюся относительно системы К с постоянной скоростью вдоль оси Ox системы К так, что оси Ox’ и Ox совпадают, а за начальный момент отсчета времени t=0 примем момент совпадения начал координат, т.е. .

Пусть, далее, координаты некоторой частицы m в системе К будут x,y,z, а в системе K’ — x’,y’,z’. Радиус-векторы частицы в этих системах отсчета связаны простым соотношением: , а, значит:

Это и есть прямые преобразования координат Галилея .

Дифференцируя их по времени, получаем классическую теорему сложения скоростей :

Повторное дифференцирование приводит к очень важному соотношению:

Его смысл очевиден: если частица в ИСО (системе К) движется неускоренно( ), то и система K’, движущаяся относительно системы К с постоянной скоростью, по определению тоже будет инерциальной.

Источник

Векторный способ описания движения

В этом случае положение частицы задается её радиус-вектором . Геометрическое место концов радиус-вектора представляет кривую,
называемую траекторией.

Зависимость радиус-вектора частицы от времени называется кинематическим уравнением движения. С геометрической
точки зрения — это уравнение траектории.

Изменение радиус-вектора за время ∆t называется перемещением: . Длина дуги траектории между этими точками ∆l назывется путем.
Важнейшей кинематической характеристикой движения является скорость.

Скоростью частицы называется векторная величина, определяемая равенством
,
иначе говоря, скорость — это производная от радиус-вектора по времени.

Из определения следует, что скорость направлена по касательной к траектории. Величина скорости
,
где l — путь, пройденный вдоль траектории.
Иногда используется понятие средней скорости: это векторная величина, равная отношению перемещения ко времени, т.е.

Скорость изменения скорости частицы по времени, т.е. вектор

называется ускорением частицы.

Таким образом, зная кинематический закон движения, можно простым дифференцированием по времени найти скорость и ускорение в любой
момент времени (так называемая прямая задача кинематики).

Наоборот, зная ускорение частицы, а также начальные условия, т.е. положение и скорость частицы в начальный момент времени,
можно найти траекторию движения частицы (обратная задача кинематики).

Координатный способ описания движения

Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение частицы в любой момент времени определяется тремя ее координатами x,y,z.Проектируя радиус-вектор на координатные оси, получим три зависимости координат частицы от времени

которые представляют кинематический закон движения в координатной форме.

Модули скорости и ускорения будут
и
Обратная задача:
и

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

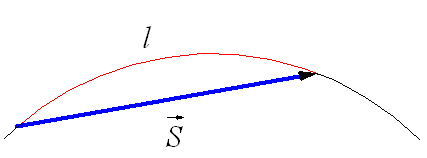
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение— это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).

Движение точки по окружности может быть очень сложным (рис. 17).

Рассмотрим подробно движение точки по окружности, при котором v = const. Такое движение называется равномерным движением по окружности. Естественно, вектор скорости не может быть неизменным (v не равно const), так как направление скорости постоянно меняется.

Время, за которое траектория точки опишет окружность, называется периодом обращения точки (Т). Число оборотов точки в одну секунду называется частотой обращения (v). Период обращения можно найти по формуле:

Естественно, перемещение точки за один оборот будет равно нулю. Однако пройденный путь будет равен 2ПиR, а при числе оборотов п путь будет равен 2ПиRn или2ПиRt/T, где t — время движения.

Ускорение при равномерном движении точки по окружности направлено к ее центру и численно равно а = v 2 /R.

Это ускорение называется центростремительным (или нормальным). Вывод этого равенства может быть следующим. Приведем векторы скорости к одной точке хотя бы за — Т (можно и за Т/2 или Т) (рис. 18).

Тогда сумма изменений векторов скоростей за малые промежутки времени будет равна длине дуги АВ, которая равна модулю |v₂ — v₁| за время t = 1/4*Т.

Определим длину дуги. Поскольку радиусом для дуги будет модуль вектора v₁=v₂=v, то длина дуги l может быть вычислена как длина четверти окружности с радиусом v:

После сокращения получим:

Если же движение равнопеременное, то v Ф const, тогда рассматривают другую составляющую ускорения, обеспечивающую изменение модуля скорости. Это ускорение называется тангенциальным:

Тангенциальное ускорение направлено по касательной к траектории, оно может совпадать по направлению со скоростью (движение равноускоренное) или быть противоположно направленным (движение равнозамедленное).

Источник