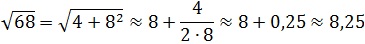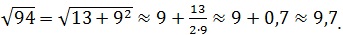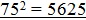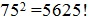Вавилонский способ извлечения квадратного корня

Информационно-коммуникационные технологии
в педагогическом образовании

НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ

К. Б. Милюхина

Муниципальное бюджетное общеобразовательное учреждение Лесоперевалочная СОШ № 2, с. Бельтирское, Аскизский район

НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ

Аннотация. Тема, затронутая в статье, показывает, что изучение квадратных корней, не прихоть математиков, а объективная необходимость: в реальной жизни случаются ситуации, математические модели которых содержат операцию извлечении квадратного корня. Изучив способы извлечения квадратного корня, был создан проект «Несколько способов извлечений квадратных корней».

1-й способ: Способ разложения на простые множители [1]

Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения (табл.).

Ученики применяют этот способ успешно и считают единственным. Извлечение корня разложением на множители – трудоёмкая задача, которая не всегда приводит к желаемому результату. Попробуем извлечь квадратный корень из числа 206116. Разложение на простые множители дает произведение 2∙2∙51529. А как быть дальше? В ответе записывают остаток от разложения под знак корня. Чаще мы видим, что корень до конца не извлечь. Поэтому, этот способ лишь частично решает проблему извлечения квадратного корня.

2-й способ: Способ использования таблицы квадратов двузначных чисел [1]

Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых.

Найдём значение .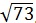

Закрываем две последние цифры у всех чисел в таблице квадратов и находим близкие для 73, таких два числа 7225 и 7396 (7396-это много). Рассматриваем число 7225.

Левый столбик таблицы квадратов даёт ответ 8 (целых), а верхняя строка 5 (десятых). Значит .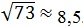

Быстро, просто, доступно на экзамене. Корни большие 100 этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.

3-й способ: Формула Древнего Вавилона [4]

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа Х.

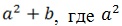
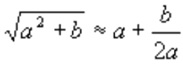
Число Х они представляли в виде суммы ближайший к числу Х точный квадрат натурального числа a и пользовались формулой (1).

(1)

Извлечём с помощью этой древней формулы корень квадратный из числа 68:

Результат извлечения корня из 68 с помощью МК равен 8,246211.

Результат извлечения корня из 94 с помощью МК равен 9,695359.

Как видим, способ вавилонян даёт хорошее приближение к точному значению корня. Но без знания полных квадратов больших чисел и умения их быстро находить, результат извлечения будет найти затруднительно.

Этот способ являются самым простым и доступным для учащихся школ.

4-й способ: С помощью уравнения [2]

Существует удобный способ нахождения квадратного корня с помощью решения уравнения. В чем его суть рассмотрим на примере и попробуем вычислить значение корня из числа 37.Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа .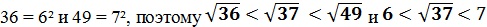

Пусть х – это та разница, на которую отличны друг от друга ,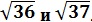

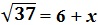
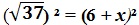
значит . Возведем в квадрат обе части полученного уравнения и раскроем скобки при помощи формулы квадрата суммы:

37 = (6 + х)² = 36 + 12х + х².

Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.

В результате приходим к простому линейному уравнению 37 = 36 + 12х.

Решив его, получаем значение: х = 0,08. Значит .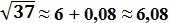

Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.

5-й способ: Канадский метод [5]

Канадский метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух-трёх знаков после запятой. Применяли формулу:

(2)

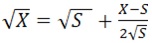
где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.

Например: извлечь квадратный корень из 86

.

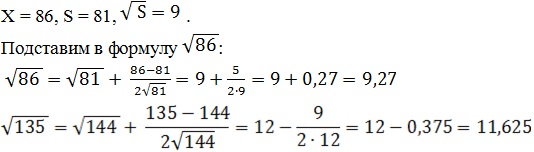
Метод несложный и удобный.

6-й способ: Способ вычетов нечётного числа [3]

Способ вычетов нечётного числа заключается в том, чтобы из подкоренного выражения последовательно вычитать нечётные числа 1, 3, 5, 7 и т. д. пока разность не станет равной 0, а затем подсчитать количество вычитаний. Это и будет ответ.

Например: извлечь квадратный корень из 81.

Решение: 81-1=80-3=77-5=72-7=65-9=56-11=45-13=32-15=17-17=0, количество вычитаний = 9, поэтому .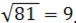

Например: извлечь квадратный корень из 225.

количество вычитаний = 15, поэтому .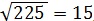

Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности. Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.

7-й способ: Способ отбрасывания полного квадрата (для четырёхзначных чисел) [3].

Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.

1) Извлечение корней до числа

Например: .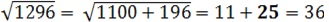

Число 1296 представим в виде суммы, выделив из этого числа квадрат 196, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (11) прибавляем всегда 25. Получим ответ 36.

Так можно извлекать только квадратные корни до числа

2) Извлечение корней после числа

Например: .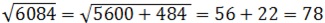

Число 6084 представим в виде суммы 5600 и выделенного квадрата 484. Затем к числу сотен прибавить квадратный корень из 484, равный 22.

Получим ответ 78.

Этот способ очень интересен и оригинален.

Применим только для четырёхзначных чисел точных квадратов.

Список литературы

1. Мордкович, А. Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учебник для общеобразовательных учреждений [Текст]. / А. Г. Мордкович. – М.: Мнемозина. – 2012.
2. Пичугин, Л. Ф. За страницами учебника алгебры. Книга для учащихся 7–9 классов средней школы [Текст]. / Л. Ф. Пичугин. – М.: Просвещение. – 1990.
3. Научно-теоретический и методический журнал «Математика в школе», 1998. – № 6.
4. Теорема [Электронный ресурс]. // Википедия: свободная энциклопедия. – Режим доступа : http://ru.wikipedia.ord/wiki/Теорема
5. Открытый урок [Электронный ресурс]. // Первое сентября. – Режим доступа : http://festival.1september.ru/

Научный руководитель: учитель математики
Сердюк С. А.

Комментарии: 1

Андрей из Чебоксар 28.05.2020 в 19:15

5-й способ: Канадский метод
Так и хочется дописать:
Канадский метод был открыт молодыми учёными одного из ведущих университетов ДРЕВНЕГО ВАВИЛОНА (см. способ 3)

Источник

Методы извлечения квадратного корня

Министерство образования Республики Башкортостан

Муниципальное общеобразовательное бюджетное учреждение «Гимназия №2 с. Бураево»

муниципального района Бураевский район

гимназии«Шаг в будущее»

извлечения квадратного корня

Учебно – исследовательская работа

Авторы Гиззатуллина Ляйсан ,

Гильмутдинова Регина, обучающиеся 8Б класса

МОБУ Гимназия №2 с.Бураево

Руководитель Ситдикова И.М., учитель

математики МОБУ Гимназия №2 с.Бураево

Методы извлечения квадратного корня…………………………. 5

Метод геометрических построений ………………..……. …. 10

Извлечение квадратного корня столбиком……………………. 11

Результаты исследования………. ………………………..…………….13

Библиографический список…………………………………………………. 15

Правильному применению методов можно научиться, только применяя их на разнообразных примерах.

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека.

Актуальность данного исследования определяется следующими обстоятельствами. Математические модели многих практических задач представлены различными видами уравнений, в решении которых приходится сталкиваться с квадратными корнями. На олимпиадах, итоговой аттестации приходится извлекать квадратные корни без использования калькулятора, таблицы квадратов для двухзначных чисел. Владение методами извлечения квадратных корней сокращает время для выполнения задания, от которого зависит результат выполнения работы, процесса обучения.

Цель работы сопоставление различных способов приближенного извлечения квадратных корней, выявление наиболее эффективного способа в зависимости от поставленной задачи.

Исходя из поставленной цели, в работе определены следующие задачи:

изучить литературу и Интернет-ресурсы по данной теме.

познакомиться с историей извлечения квадратных корней;

рассмотреть методы извлечения квадратных корней;

провести исследование по выявлению способов извлечения квадратных корней, которыми владеют старшеклассники школы.

Объектом исследования являются квадратные корни , а предметом – методы извлечения квадратных корней.

Основными методами исследования были: анкетирование, сбор информации, анализ.

Навыки исследовательской деятельности, поиска и обработки информации, выбора способа представления результатов, полученных в работе, умение извлекать квадратные корни различными способами помогут в обучении, при решении исследовательских задач, при подготовке к итоговой аттестации, в профессиональной деятельности, что является актуальным для учеников школы.

Теоретическая значимость исследования состоит в систематизации основных методов извлечения квадратных корней и составлении алгоритмов для их вычисления.

Практическая значимость – разработан буклет-памятка по данной теме для возможного использования в учебном процессе.

1. ИСТОРИЯ КВАДРАТНОГО КОРНЯ

Квадратным корнем из числа a называют такое число, квадрат которого равен a. Например, числа -5 и 5 являются квадратными корнями из числа 25. То есть, корни уравнения x 2 =25, являются квадратными корнями из числа 25.

Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен а. В нашем примере, это буде т число 5. Процесс нахождения арифметического квадратного корня называют извлечением квадратного корня.

Арифметический квадратный корень имеет свое обозначение. Его обозначают так: . Знак называют знаком арифметического квадратного корня. Выражение, которое записано под знаком корня, называют подкоренным выражением.

Интересная история современного обозначения корня, а также самого названия «корень». Индийцы называли его «мула» – корень (дерева), основание, начало; арабы – «джузр» – корень, основание квадрата, а европейцы, сохранив смысл, перевели его на латынь. Так появилось название radix (по-латыни «корень»), отсюда – радикал. Сначала обозначение корня сократили до Rx, затем до строчной буквы r. Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году. В дальнейшем буква r трансформировалась в знак . Рене Декарт в 1637 году объединил его с горизонтальной чертой, которую ставили над подкоренным выражением, в результате появился современный знак.

Существует неофициальный праздник, посвященный квадратному корню. День квадратного корня — праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: 02-02-04).

Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81). Основателем праздника является школьный учитель Рон Гордон из Калифорнийского города Редвуд Сити в США. Главным блюдом в этот день на «праздничном столе» обычно являются вареные кубики из овощей и выпечка в форме математического знака квадратного корня.

По объективным математическим причинам этот праздник может отмечаться строго девять раз в столетие (семь раз в первой половине века и дважды — во второй), всегда в одни и те же дни:

1 января **01 года

2 февраля **04 года

3 марта **09 года

4 апреля **16 года

8 августа **64 года

9 сентября **81 года

При этом интересно заметить, что промежуток (в годах) между праздниками составляет непрерывную последовательность нечётных чисел: 3, 5, 7 и т. д. .

2. МЕТОДЫ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ

В ходе данного исследования были выявлены следующие методы извлечения квадратного корня .

Источник