Вариативный подход к решению арифметических задач
статья по математике на тему
Вариативный подход к решению арифметических задач
В условиях стремительных изменений в обществе меняются и требования к современному ученику. Он должен обладать более широкими взглядами на жизнь, большим спектром вариантов выхода из предлагаемых ситуаций, быть более мобильным. И основная задача в формировании навыков вариативности ложится на плечи учителя начальных классов, так как именно он определяет основные принципы учебной деятельности. Креативный подход к учебному материалу должен стать неотъемлемой частью всей учебной деятельности обучающегося, красной линией проходить через весь процесс обучения и воспитания. И как нельзя лучше для начального обучения вариативности подходят уроки математики.
Скачать:
| Вложение | Размер |
|---|---|
| variativnyy_podhod_k_resheniyu.docx | 129.1 КБ |
Предварительный просмотр:
Вариативный подход к решению арифметических задач
В условиях стремительных изменений в обществе меняются и требования к современному ученику. Он должен обладать более широкими взглядами на жизнь, большим спектром вариантов выхода из предлагаемых ситуаций, быть более мобильным. И основная задача в формировании навыков вариативности ложится на плечи учителя начальных классов, так как именно он определяет основные принципы учебной деятельности. Креативный подход к учебному материалу должен стать неотъемлемой частью всей учебной деятельности обучающегося, красной линией проходить через весь процесс обучения и воспитания. И как нельзя лучше для начального обучения вариативности подходят уроки математики.
Так, при работе с текстовыми задачами могут быть использованы разные приемы. Учителя, как правило, не останавливаются на этом из-за нехватки времени на уроке, переходят к следующему заданию. Эту же проблему поднимает и Л.В.Болотник в своей книге «Дидактические возможности учебников по математике для начальной школы». Покажем эти приемы на примере решения одной составной задачи. Мы их подразделяем на две группы.
I. 1. Придумай задачу, обратную данной.
Такой прием заставит ученика не только еще раз вернуться к содержанию задачи и осмыслить логику решения и принципы построения задачи, но и построить собственную, обратную логическую цепь рассуждений и умозаключений, организуемых в условии новой задачи. Например:
С первого участка собрали 98 килограммов картофеля. Со второго – на 6 килограммов больше, чем с первого. Сколько килограммов картофеля собрали с третьего участка, если всего собрали 270 килограммов картофеля?
Задача, обратная данной, будет звучать так:
С первого участка собрали 98 килограммов картофеля, со второго – на 6 килограммов больше, чем с первого, а с третьего – на 30 килограммов меньше, чем с первого. Сколько килограммов картофеля собрали со всех трех участков?
2. Поиск различных способов решения.
Следует отметить, что этот прием подходит только для тех задач, которые имеют несколько способов решения. Здесь важно показать ученику логику решения каждым из способов, дать сравнительную характеристику решений, проанализировать ход решения каждого способа. Тогда решение вышеприведенной задачи будет выглядеть следующим образом.
1) 98 + 6 = 104 (кг) – со II участка;
2) 270 – 98 = 172 (кг) – со II и III участков;
3) 172 – 104 = 68 (кг) – с III участка.
Запишем это решение выражением:
270 – 98 – (98 + 6) = 68 (кг) – с III участка.
- 98 + 6 = 104 (кг) – со II участка;
- 98 + 104 = 202 (кг) – с I и II участков;
- 270 – 202 = 68 (кг) – с III участка.
Выражение этого решения будет выглядеть так:
270 – [98 + (98 + 6)] = 68 (кг) – с III участка.
3. Решение задачи через введение переменной.
Такой прием позволяет уже на ранних этапах обучения математике знакомить детей с уравнением, закрепляет их знания в области поиска «неизвестного». Например, чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Аналогично по ситуации проговариваются все действия с арифметическими компонентами действий. Такая работа позволяет закрепить алгоритм нахождения неизвестного, абстрагировать процесс его нахождения.
Обозначим через х количество картофеля, собранного с III участка. Тогда будет такое уравнение: 270 = 98 + 104 + х.
4. Составление аналогичной задачи с новыми данными.
Этот прием помогает детям переносить уже известную схему решения на другие задачи этого вида, учит обобщать их в группы.
В магазине игрушек на полках стояло 560 игрушек трех видов. Слоников было 111 штук, а медвежат – на 45 штук больше. Сколько на полках было лисят?
5. Постановка дополнительных вопросов к решенной задаче.
Подобная работа предполагает постановку дополнительных вопросов, замену известных величин неизвестными и поиск новых решений, стимулирует мысль ученика, заставляет его анализировать и сравнивать несколько схем решения задач. Например:
«Как изменился бы ход решения задачи, если бы было не известно, сколько килограммов картофеля собрано со II участка, при известной массе картофеля, собранной с I и III участков? На сколько больше килограммов картофеля собрали с I участка, чем с III? На сколько больше килограммов картофеля собрали с I и II участков вместе, чем с III?»
6. Записать решение задачи выражением.
Подобная работа помогает ребенку не только увидеть решение задачи в целом, но и закрепить порядок записи арифметических действий, навык грамотного использования скобок и двойных скобок. Применительно к нашей задаче выражение будет выглядеть так:
270 – 98 – (98 + 6) = 68 (кг) – с III участка.
Или: 270 – [98 + (98 + 6)] = 68 (кг) – с III участка.
II.1. Составление задачи по выражению.
Например, по выражению 6 – 3 можно составить задачи на нахождение меньшего, остатка, разницы.
На нахождение меньшего:
У Димы было 6 машинок, а у Пети – на 3 меньше. Сколько машинок было у Пети?
На нахождение разницы:
У Димы 6 машинок, а у Пети – 3. На сколько машинок у Димы больше, чем у Пети?
На нахождении остатка:
У Димы было 6 машинок. Он подарил Пете 3 машинки. Сколько машинок у него осталось?
Использование схем при решении составных задач (когда составную задачу расчленяют на простую) помогает даже слабоуспевающим ученикам разбираться в задачах, устанавливать взаимосвязь между величинами.
Например, возьмем задачу на пропорциональную зависимость.
В 4 одинаковых ящиках было 28 кг апельсинов. Сколько килограммов апельсинов в 8 таких ящиках?
Вначале составляем краткую запись задачи в виде схемы. Дети работают в тетрадях, используя разные цвета, а учитель – на доске с цветными мелками.
Перед учителем всегда должен стоять вопрос, как провести необходимое для поиска решения задачи рассуждение наиболее доступным младшему школьнику образом. Сначала нужно выявить зависимости между величинами.
Рассуждение начинаем с главного вопроса задачи. Возьмем красный цвет и выделим главный вопрос задачи квадратиком прямо на ее краткой записи. Ставиться вопрос: что нужно, чтобы найти массу 8 ящиков? (Используем схему). Красным цветом от главного вопроса задачи ведем 2 стрелки: к числу 8 (количество ящиков) и к знаку вопроса (масса 1 ящика). Вычленилась простая задача. Неизвестна масса 1 ящика. Знак вопроса обводим зеленым кружочком. Теперь ставится вопрос: что нужно сделать, чтобы найти массу 1 ящика? Зеленым цветом ведем стрелки к числам 4 (количество ящиков) и 28 кг (масса всех ящиков). Затем на краткой записи устанавливаем порядок действий (обратный ход), в кружочках отмечаем порядок действий. Таким образом, отчетливо видно, что составная задача имеет 2 действия решения. Использование разных цветов помогает устанавливать количество действий задачи и взаимосвязь между величинами.
В конце вычленяем простые задачи:
Представление составной текстовой задачи в виде последовательной цепочки простых задач способствует развитию логического мышления.
Обучение детей младшего школьного возраста аналитическому способу рассуждения при решении задач уместно начинать с задач в два действия, затем постепенно усложнять их.
Для лучшего усвоения взаимосвязи между величинами полезно решать с разбором задачи с буквенными данными. Например, рассмотрим задачу на движение:
Аня шла к часов со скоростью х км/ч, а Полина – а часов со скоростью у км/ч. На сколько километров больше прошла Полина, чем Аня?
х · к – SА; 2) у · а — SП; 3) у · а – х · к – на? > .
Такая методика работы над задачей способствует развитию у детей умения мыслить. Действительно, математические рассуждения с присущими им четкостью, последовательностью и логичностью являют собой пример правильно организованного мышления, а владение математическим языком, понимание точного смысла утверждений и связей между логическими конструкциями в тексте задачи оказывают существенное влияние на языковое развитие личности и тем самым вносят весомый вклад в формирование и развитие мышления человека в целом.
Применение предлагаемых приемов работы над текстовой задачей формирует еще и такое немаловажное качество личности, как умение рассуждать.
Таким образом, научить простейшим операциям анализа, синтеза, сравнения на примере решения текстовых задач с целью перенесения усвоенных знаний, умений, навыков в другие сферы деятельности обучающихся – и есть первостепенная задача учителя начальных классов. Для этого необходимо:
1) научить детей находить нужные умозаключения, чему, собственно, и учит математика;
2) научить располагать эти умозаключения в правильном порядке.
Таким образом, формирование вариативного подхода к решению текстовых задач имеет глубокие цели и задачи, ведет в конечном итоге к формированию конкурентоспособной личности выпускника школы.
По теме: методические разработки, презентации и конспекты
Актуальность темы обусловлена обновлением содержания обучения, где одним из ведущих процессов является формирование у школьников приёмов самостоятельного приобретения знаний, формирование акти.
Урок структуирован по новым требованиям ФГОС НОО, содержит основные этапы, формирование предметных умений и универсальных учебных действий на каждом этапе урока. На уроке используется сист.
Конспект урока математики в 3 классе УМК «Гармония».
КУонспект урока математики в 3 классе.
Презентация к уроку математики в 3 классе по УМК «Гармония».
Для эффективности усвоения приёмов проверки решения задач и вычислений разработаны памятки, содержащие систему операций.
Школа не только учит, она готовит учащихся к самостоятельной жизни, формирует их как личность, поэтому беседы нравственного характера очень важны. Нравственное воспитание может и должно осуществляться.
Источник
Вариативные задачи
Постановка проблемы. Анализ школьных учебников геометрии выявил задачи, которые имеют неоднозначное решение, а в условии или требовании задачи нет прямого указания на возможные варианты решений. Правильность решения таких задач зависит от подготовки учителя, от наличия у него умения «видеть» задачу в различных вариантах. У учащихся, в случае получения различных ответов, возникает сомнение в правильности постановки задачи. И со всеми вопросами они вновь обращаются к учителю, который зачастую не готов дать исчерпывающий ответ. Лишь хорошо подготовленный преподаватель приходит к правильному решению такого рода задач. Это задачи, допускающие неоднозначное решение, – вариативные задачи. Они не выделены в особый класс, поэтому очень часто происходит потеря решений. Однако именно вариативные задачи наиболее значимы для развития критичности мышления, комбинаторных способностей учащихся, создают ситуации побуждения к более вдумчивому анализу заложенной в задаче информации и ее структурированию. Задачи указанного типа приближены к жизненно-практическим условиям, так как любая жизненная ситуация как правило имеет несколько вариантов исхода. Вариативные задачи создают условия для выработки собственного взгляда на ситуацию и переносят акцент с самого процесса усвоения знаний на их осмысление, наполнение личностным смыслом, что, в свою очередь, обеспечивает более эффективное усвоение знаний.
В методической литературе задачам выделенного типа не уделяется должного внимания. Феномен вариативных задач изучен недостаточно. В учебно-методической литературе встречаются примеры многовариантных задач. Но на сегодняшний день не разработаны рекомендации, эвристики, позволяющие застраховать учащихся от неполных решений. Использование большого количества вариативных задач в учебниках нового поколения только доказывает необходимость изучения методики их решения.
Понятие вариативной задачи. В большем числе случаев геометрические задачи школьных учебников имеют однозначное решение. В этом мы сами убедились, проанализировав учебники геометрии под редакцией А.В. Погорелова и Л.С. Атанасяна. Из общей массы задач всего порядка десятка имеют интересующую нас характеристику – несколько вариантов решения, влекущих за собой различные ответы. Именно такие задачи мы и будем называть вариативными.
Под вариативной будем понимать задачу, у которой формулировка не допускает точного установления взаимного расположения объектов условия или требования.
Отличие вариативной задачи от стандартной можно представить схематично.
Стандартная задача Вариативная задача
 |
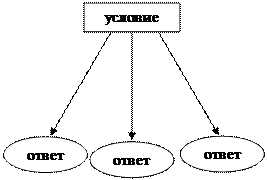 |
Решить вариативную задачу значит рассмотреть все возможные варианты расположения объектов. Например, в задаче: «На книжной полке стоит двухтомник. Толщина страницы составляет 0,05 мм, а толщина обложки – 1 мм. В первом томе 320 страниц, а во втором – 400. Жучок прогрыз две книги от первой страницы первого тома до последней страницы второго. Какое расстояние он при этом прополз?» возможны два решения в зависимости от того, как стоят книги.
Не рассматривая различные варианты расположения искомой фигуры невозможно решить задачу: «Постройте квадрат по двум данным вершинам А(0,0); К(-2,4)». Чем будет являться отрезок АК – диагональю или стороной искомого квадрата? Отвечая на подобные вопросы, ученики учатся рассматривать все возможные варианты заданной в задаче ситуации, то есть приучаются к «полноте дизъюнкции».
Полонский В.Б., Рабинович Е.М., Якир М.С. выделяют условия, ведущие к неоднозначной трактовке задачи:
1. Условие задачи не определяет взаимное расположение точек и фигур:
а) точка или принадлежит отрезку АВ, или ему не принадлежит, но лежит на прямой АВ; б) точки лежат или в одной полуплоскости относительно заданной прямой, или в разных (то же с полупространством); в) различные расположения центра описанной окружности или ортоцентра треугольника в зависимости от вида треугольника.
2. В условии задачи фигурируют две касающихся окружности, но не указан способ касания: внешний или внутренний. В задаче даны две точки, делящие окружность на две дуги, кроме того, известно, что некоторая прямая касается окружности, но не указано на какой из двух дуг лежит точка касания.
3. В задаче фигурируют объекты, которым приписываются определенные свойства, но не указан порядок соответствия между множеством объектов и множеством их свойств: а) сказано, что АВС – равнобедренный треугольник, но не сказано, какие пары сторон равны; б) точка М делит отрезок АВ на отрезки длинной а и b, при этом не уточняется, какой из них равен а, а какой b; в) известно, что угол между пересекающимися прямыми АВ и CD равен a, однако, не указано, который из углов – AMD или АМС (М – точка пересечения прямых) – острый.
Возможны и другие причины возникновения вариативности. Например, при решении задачи: «Постройте треугольник по двум сторонам и углу, прилежащему к одной из них» можем получить два треугольника, удовлетворяющих требованию задачи.
 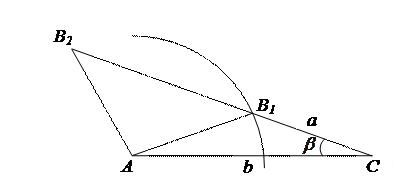 | Ни одно из условий, выделенных авторами книги //, не объясняет два ответа в данной задаче. Кроме того, не выделены особенности возникновения вариативности в алгебраических зада- |
чах. (Например, в задачах на прогрессию очень часто получаются два ответа.)
Конструирование вариативных задач. Получить вариативную задачу можно из стандартной задачи учебника. Для этого нужно разбить условие и требование задачи на объекты и их характеристики, убрать некоторые из них и проверить на корректность.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник




