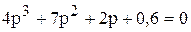Устойчивость способы определения устойчивости

1.2 Методы определения устойчивости

Устойчивость линейных систем не зависит от величины возмущения; система, устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях. Поэтому для суждения об устойчивости линейных систем достаточно исследовать и определить устойчивость «в малом», т. е. найти устойчивость по уравнениям в форме приращений. При этом судить об устойчивости можно по корням характеристического уравнения замкнутой системы.

Если динамика системы точно описывается линейным дифференциальным уравнением с постоянными коэффициентами, то устойчивость «в малом» обеспечивает неограниченную устойчивость системы. Нелинейные системы, описываемые нелинейными дифференциальными уравнениями, могут быть устойчивыми при малых возмущениях и неустойчивыми при больших.

Процессы, происходящие в большей части реальных систем, описываются нелинейными дифференциальными уравнениями, которые для упрощения исследования могут быть линеаризованы. Тогда исследование реальной (действительной) системы заменится исследованием линеаризованной системы.

1.2.1 Оценка устойчивости по критерию Ляпунова

Правильность суждения об устойчивости реальной системы «в малом» по линеаризованным уравнениям доказана А. М. Ляпуновым.

При некоторых общих условиях справедливо следующее (первая теорема А. М. Ляпунова).

1Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то действительная система устойчива. При этом никакие отброшенные при линеаризации члены второй и высших степеней отклонения переменных не могут изменить устойчивость системы.

2Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то действительная система неустойчива. При этом никакие отброшенные при линеаризации члены второй и высших степеней отклонения переменных не могут придать системе устойчивость.

3Если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или пару чисто мнимых сопряженных корней, то поведение действительной системы не может определяться ее линеаризованным уравнением. В этом случае отброшенные при линеаризации уравнения члены второй и высшей степеней отклонения переменных коренным образом изменяют описание динамического процесса реальной системы.

Аналитическая формулировка условия устойчивости сводится к тому, что возникшая в результате нарушения равновесия абсолютная величина отклонения управляемой переменной от заданного значения (ошибка x)по истечении достаточно длительного промежутка времени должна стать меньше некоторого заранее заданного значения:

Для астатической системы ошибка регулирования равна нулю, поэтому =0. При аналитическом исследовании динамических свойств автоматической системы надо составить для нее дифференциальное уравнение и проинтегрировать его. Это означает, что будет найден закон изменения интересующей нас переменной во времени, согласно которому можно сделать заключение о характере переходного процесса (устойчивый или неустойчивый).

Для решения указанной задачи необходимо найти свободное движение системы, которое описывается однородным дифференциальным уравнением:

x_св(t) — свободное движение системы, определяющее динамическую ошибку.

На основании дифференциального уравнения можно записать характеристическое уравнение системы:

Характеристическое уравнение определяет корни, характеризующие свободное движение. Известно, что при отрицательных вещественных корнях составляющая свободного движения при tмонотонно убывает до нуля, как показано на рисунке 1.1, а. Для пары комплексных корней с отрицательной вещественной частью составляющая свободного движения приtтакже убывает до нуля по закону затухающих колебаний (рисунок 1.1, б).

Рисунок 1.1 — Переходные процессы при различных корнях характеристического уравнения

Аналитические выражения для составляющих свободного движения:

где A_i,A_j — постоянные интегрирования, определяемые из начальных условий;

р_i,j — корни характеристического уравнения;

_i,j — вещественная часть корня (интенсивность затухания колебаний);

_j — мнимая часть корня (частота собственных колебаний);

Система будет устойчивой при отрицательных корнях и отрицательных вещественных частях корней. В случае положительного вещественного корня составляющая свободного движения при tбудет неограниченно возрастать (рисунок 1.1, в). Для пары комплексных корней с положительной вещественной частью составляющая свободного движения приtтакже будет возрастать по закону расходящихся колебаний (рисунок 1.1, г).

Если среди корней характеристического уравнения будет хотя бы одна пара чисто мнимых, то появится составляющая свободного движения в виде незатухающего колебательного процесса и система будет находиться на границе устойчивости и неустойчивости.

Таким образом, для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения замкнутой системы D(p) лежали слева от мнимой оси комплексной плоскости корней.

Значения коэффициентов характеристического уравнения, при которых по крайней мере одна пара комплексных корней находится на мнимой оси, а все остальные корни расположены в левой полуплоскости, определяют границу устойчивости. Граница устойчивости делит совокупность значений коэффициентов характеристического уравнения на две области: одна соответствует устойчивости системы, другая — неустойчивости.

Анализируя коэффициенты уравнения, можно установить, что они зависят только от постоянных времени и коэффициентов усиления звеньев системы.

Возникновению неустойчивости, как правило, способствует увеличение коэффициента усиления системы. В некоторых частных случаях уменьшение этого коэффициента может привести к нарушению устойчивости. Такие системы называются условно устойчивыми.

Для суждения об устойчивости структурно устойчивых линейных систем надо определить расположение корней характеристического уравнения на комплексной плоскости. При этом можно не вычислять корни характеристического уравнения, надо лишь выяснить, все ли корни расположены слева от мнимой оси.

Обычно встречаются две постановки этой задачи:

1) можно считать, что заданы все параметры системы, и необходимо определить, устойчива ли система при этих значениях параметров (задача анализа);

2) необходимо определить значения некоторых параметров (при заданных остальных), при которых система устойчива (задача синтеза).

Математическая формулировка условий, которым должны удовлетворять коэффициенты характеристического уравнения или какие-либо функции этих коэффициентов, чтобы система была устойчивой, называется критерием устойчивости. Критерии устойчивости делятся на алгебраические и частотные; они позволяют выяснить, все ли корни характеристического уравнения замкнутой системы находятся в левой полуплоскости без решения этого уравнения.

Необходимым условием устойчивости линейной системылюбого порядка является положительность всех коэффициентов характеристического уравнения этой системы.

Пусть имеется характеристическое уравнение замкнутой системы

Это уравнение можно представить в виде произведения множителей, содержащих корни:

Если все корни характеристического уравнения будут отрицательными, то все множители будут положительными:

Производя перемножения в (1.7), получают (1.5), в котором все коэффициенты будут определяться положительными членами уравнения (1.7), т. е. будут положительными; нигде не могут получиться отрицательные числа и нули.

Аналогичное явление можно установить, если имеются комплексные корни с отрицательной вещественной частью:

Уравнение (1.8) также приводится к виду уравнения (1.5) с положительными коэффициентами. Для того чтобы получить отрицательные вещественные части корней, необходимо условие положительности всех коэффициентов уравнения.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Методы определения устойчивости

Для того, чтобы система была устойчивой, должны выполняться определенные условия, которые называются условиями устойчивости. Все условия устойчивости разделяются на необходимые и достаточные.

Н е о б х о д и м о е условие устойчивости.Если это условие соблюдено система может быть как устойчивой, так и неустойчивой если же условие не соблюдается, то система наверняка неустойчива, и продолжение исследований на устойчивость теряет смысл. Хотя это условие не дает ответа на вопрос “устойчива система или нет”, оно позволяет на начальном этапе работ исключить заведомо непригодные варианты. Поэтому при исследовании устойчивости сначала проверяют соблюдение необходимого условия. Необходимым условием устойчивости системы является положительность всех коэффициентов ее характеристического уравнения. При этом равенство нулю хотя бы одного коэффициента также является нарушением необходимого условия.

Например, для системы с характеристическим уравнением

необходимое условие удовлетворяется, и исследование ее на устойчивость должно быть продолжено. А вот системы с характеристическими уравнениями

,

заведомо неустойчивы, так как в первой системе один коэффициент равен нулю, а во второй имеется отрицательный коэффициент.

Д о с т а т о ч н о е условие устойчивости.Это условие дает однозначный ответ на вопрос об устойчивости системы, если известны значения всех корней.

Достаточным условием устойчивости системы является отрицательное значение вещественной части всех корней ее характеристического уравнения.

Но, к сожалению, вычисление корней уравнений высоких степеней настолько сложно, что для исследования устойчивости предпочитают использовать специальные методы косвенных оценок. Эти методы позволяют оценить устойчивость системы по коэффициентам ее характеристического уравнения без вычисления корней. Такие оценки носят название “критерии устойчивости”.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Определение устойчивости систем автоматического управления промышленными роботами

Введение

Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].

Постановка задачи

Теория просто и кратко

Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):

(1)

где и – соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.

Замкнутая САУ устойчива, если комплексная частотная функция , начинаясь на
стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.

(2)

Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)

САУ электроприводом манипулятора промышленного робота (МПР)

Рисунок 2 – Структурная схема САУ электроприводом МПР

Передаточная функция данной САУ имеет следующее выражение [2]:

(3)
где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: .

Численные значения в выражение передаточной функции следующие:

K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.

Далее запишем характеристический многочлен замкнутой системы

заменив s на :
(4)

Решение на Python

Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:

Где I мнимая единица, w- круговая частота, T1= Tу = 0.01 ,T2= Tм = 0.1
Получим развёрнутое выражение для многочлена:

Характеристический многочлен замкнутой системы –
-I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1

Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:

Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w

Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:

Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:

Характеристический многочлен замкнутой системы — -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w

Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.

Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:

Начальная точка М(1,0)

САУ сварочного робота

Рисунок 3. Структурная схема САУ позиционированием НСУ

Характеристическое уравнение данной САУ будет иметь вид [1]:

где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.

Далее путём замены s на , получим функцию Михайлова:
(5)

Решение на Python

Характеристический многочлен замкнутой системы — w**4 — 6*I*w**3 — 11*w**2 + 46*I*w + 21
Начальная точка М(21,0)
Действительная часть Re= w**4 — 11*w**2 + 21
Мнимая часть Im= -6*w**3 + 46*w

Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.

Выводы

При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.

Источник