Устный счет все способы

Эффективные способы быстрого счета в уме

Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и неглупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».

Способы быстрого счета

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

Вычитание 7, 8, 9

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

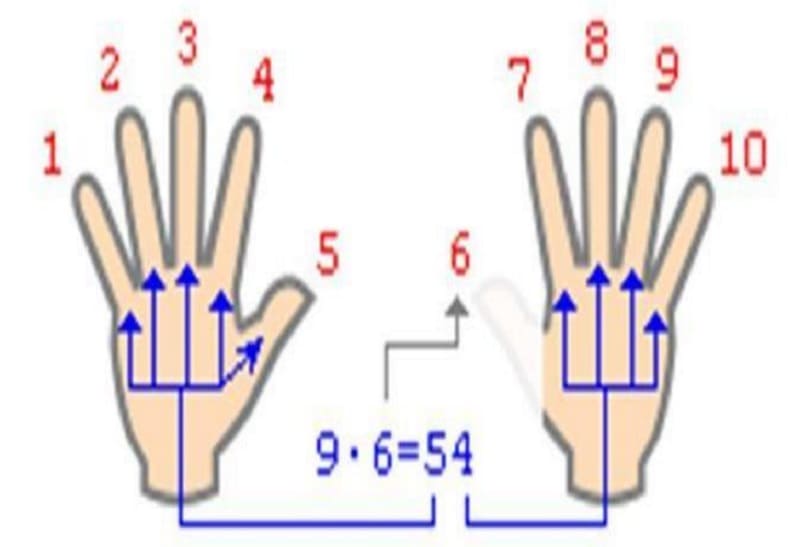
Умножение на 9

Быстро умножить любое число на 9 можно при помощи пальцев рук.

Деление и умножение на 4 и 8

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

Умножение на 5

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

Умножение на 25

Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.

Умножение на однозначные числа

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7.

Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов

Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).

Раскладка на десятки и единицы

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752

Частные методики умножения двузначных чисел до 30

Преимуществом трех способов умножения двузначных для устного счета состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.

Умножение на 11

Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.

Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.

Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.

Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа.

Например: 324 * 11=3(3+2)(2+4)4=3564

Квадрат суммы, квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

23²= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529

69² = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5.Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.

25² = (2*(2+1)) 25 = 625

85² = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

155² = (15*(15+1)) 25 = (15*16)25 = 24 025

Методика умножения чисел до 20 очень проста:

16*18 = (16+8)*10+6*8 = 288

Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода. По сути, этот метод является частным способом использования опорных чисел . В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100…

Опорное число

Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.

Для того, чтобы узнать их произведение, нужно совершить следующие операции:

15*18

1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.

Опорное число при умножении чисел до 100.Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:

47*48

1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или
из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256

50 (опорное число)

Если числа меньше опорного, то из первого множителя вычитаем разность между опорным числом и вторым множителем. Если числа больше опорного, то к первому множителю прибавляем разность опорного числа и второго множителя .

Одно число под опорным, а другое над.Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.

(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340

При умножении двузначных чисел из разных десятков в качестве опорного числа удобнее
брать круглое число , которое больше большего множителя.

27*89

Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).

В крайнем случае, можно воспользоваться «крестьянским» счетом. Чтобы умножить одно число на другое, допустим 21*75, нам нужно записать числа в две колонки. Первое число левой колонки 21, первое число правого столбика 75. Затем числа стоящие в левой колонке делить на 2 и отбрасывать остаток, пока не получим единицу, а числа в правой колонке умножаем на 2. Все строчки, имеющие четные числа в левой колонке вычеркиваем, а оставшиеся числа в правой колонке складываем, у нас получается точный результат.

21*75

Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.

Заключение

Как и все способы вычислений, данные методы быстрого счета имеют свои достоинства и недостатки:

ПЛЮСЫ:

1.С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать.
2. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
3.Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик.
4.Способы быстрого счета позволяют сократить время вычислений.
5.Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях.
6. Техника устного счета делает процесс вычислений более увлекательным и интересным.

МИНУСЫ:

1.Зачастую, решать пример, пользуясь способами быстрого счета, оказывается дольше, чем просто перемножать в столбик, так как приходится выполнять большее количество действий, каждое из которых проще первоначального.
2.Бывают ситуации, когда человек от волнения или еще чего-то забывает способы быстрого счета или вовсе — путается в них; в таких случаях ответ получается неправильным, а способы являются фактически бесполезными.
3.Не для всех случаев разработаны способы быстрого счета .
4.Вычисляя с использованием техники быстрого счета, нужно держать множество ответов в голове, в чем можно запутаться и прийти к ошибочному результату.

Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.

Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Источник

Устный счет: как научиться считать в уме

Математику уже за то любить следует, что она ум в порядок приводит» – говорил Михаил Ломоносов. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.

Но возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят вам научиться организовывать себя в различных жизненных ситуациях.

К примеру, они позволяют грамотно и оперативно планировать семейный бюджет, высчитывать проценты по кредитам и понимать уровень переплаты, делать более выгодные покупки и видеть экономию. Кроме того, умение считать в уме положительно сказывается на имидже интеллектуальных способностей и выгодно выделяет человека среди окружающих его «гуманитариев».

В дополнение к этому можно уверенно сказать, что устный счет служит отличной тренировкой мышления. Согласитесь: если человек будет месяцами сидеть на диване и выходить из дома разве что в магазин, через некоторое время он заплывет жиром, наберет вес и серьезно ухудшит свое здоровье. Точно так же и с мозгом – если им не пользоваться, он перестанет работать должным образом и просто-напросто атрофируется.

Так вот практика счета в уме как раз и не дает мозгу «набрать вес и заплыть жиром». Именно поэтому мы считаем, что данный «мягкий» навык требует развития и тренировки, и именно для этого мы и создали наш курс.

Содержание:

Однако чтобы более конкретно указать на важность умения считать в уме, а также на возможность овладеть этим умением, мы хотим познакомить вас с нашим курсом подробнее.

Цели и задачи курса

Задача курса состоит не просто в том, чтобы познакомить вас с понятием устного счета, обучить интересным техникам и приемам и научить считать в уме. На самом деле преследуются значительно большие цели. Перечислим лишь несколько наиболее существенных:

✔	Тренировка внимания и концентрации. Устный счет требует активизации многих интеллектуальных способностей, в том числе и умения сосредотачиваться на решении сложных задач, требующих времени. Чем больше вы будете практиковаться, тем более гибким и податливым будет ваше мышление и тем лучше вы будете сосредотачиваться, причем на совершенно любых задачах.
✔	Тренировка логического мышления. Устный счет, логика и последовательность мыслей связаны друг с другом очень тесно. Именно благодаря последним вы можете без проблем и очень даже быстро определить, что выйдет дешевле: 10 упаковок семян чиа весом 150 граммов по 280 рублей или 7 упаковок весом 180 граммов по цене 315 рублей. Порой даже нужно не столько считать, сколько рассуждать логически.
✔	Тренировка аналитического мышления. Считая, к примеру, на калькуляторе, мы, строго говоря, выполняем всего лишь одно простое действие – нажимаем на клавиши счетного устройства или сенсор смартфона. Если же мы считаем в уме, мы и производим и вычисления, и анализируем полученные данные, и продолжаем считать дальше, если это необходимо, а затем делаем заключительные выводы.
✔	Борьба с зависимостью от гаджетов. Высокотехнологичные устройства заполонили нашу жизнь. Многие не в состоянии посчитать в уме, сколько будет 37-18, не говоря уже о том, что глаза, руки и даже мысли огромного количества людей сосредоточены лишь на гаджете, которым они владеют. Устный счет не только помогает активизировать мышление, но и на время отвлекает от использования технологий и мотивирует к применению своего главного устройства – мозга.
✔	Профилактика болезней мозга. Неочевидно, неправда ли? Между тем, ученые уже давно установили, что отсутствие интеллектуальной деятельности провоцирует множество недугов, связанных с мозгом (болезнь Альцгеймера, деменция и т.д.) Если же вы будете чаще считать в уме, вы тем самым будете чаще задействовать свой мозг и нагружать его работой, что позволит предупредить серьезные проблемы.

Думаем, что этого более чем достаточно, чтобы в общих чертах понять, для чего нужно уметь считать в уме. Но что если копнуть чуть глубже и разобраться в вопросе подробнее?

Что такое устный счет и зачем он нужен?

Устный счет – процесс произведения математических операций в уме, т.е. без использования вспомогательных устройств, таких как калькуляторы, компьютеры, телефоны, смартфоны и т.п., а также без сторонних приспособлений, таких как ручка и бумага. Устный счет объединяет в себе представления человека о числах, знание арифметических алгоритмов и умение выполнять математические операции.

Но зачем же современному человеку уметь считать в уме, если перед ним открыто столько возможностей этого не делать? К тому же сегодня устный счет все чаще оказывается ненужным, особенно когда дело касается нынешних школьников, выросших с планшетами в руках. Но тут важно вспомнить о том, что как только мы перестаем считать в уме, мы перестаем развиваться, и это касается не только подрастающего поколения.

Все мы знаем, что мозг составляют два полушария. Правое отвечает за интуитивное мышление, художественное восприятие и творчество. Левое же отвечает за логику, речь, память, аналитику. И чем больше в мозге нейронных связей между полушариями, тем полноценнее и гармоничнее он развит. А каким образом можно развивать эти межполушарные связи? Именно таким способом и является устный счет.

Цель ментальной арифметики – натренировать мозг человека на максимально быструю обработку информации. И эти тренировки дают свою плоды, ведь благодаря специальным заданиям гармонично развиваются оба полушария мозга, вследствие чего намного легче и проще воспринимается как гуманитарная, так и техническая информация.

Особое внимание в ментальной арифметике уделяется именно устному счету, служащему эффективным тренажером для мозга. И не нужно быть гением, чтобы понять, какие преимущества имеет развитый мозг и развитое мышление. Они пригождаются везде, всегда и в любой области жизни.

Посему можно заключить, что такой, казалось бы, «простенький» или «обычный» навык, как умение считать в уме, способен повлиять на всю жизнь человека, его успехи, жизненные результаты и даже личные качества. Так что если все это имеет для вас значение, предлагаем узнать, как научиться устному счету.

Как научиться устному счету?

Есть люди, которые умеют совершать несложные арифметические операции в уме. Умножить двузначное число на однозначное, умножать в пределах 20, перемножить два небольших двузначных числа и т.д. – все эти действия они могут производить в уме и достаточно быстро, быстрее среднего человека. Часто этот навык оправдан необходимостью постоянного практического использования. Как правило, люди, которые хорошо считают в уме, имеют математическое образование или, по крайней мере, опыт решения многочисленных арифметических задач.

Несомненно, опыт и тренировка играют важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые, в отличие от вышеописанных, способны считать в уме гораздо более сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать сложные арифметические операции, которые не каждый человек и в столбик сможет посчитать.

Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме. Изучив многие подходы к обучению навыку считать устно, можно выделить три основных составляющих данного навыка:

Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации. Тренировка и опыт. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета.

Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм.

Однако не стоит недооценивать важность первых двух составляющих, поскольку, имея в своем арсенале способности и набор нужных алгоритмов, вы сможете «переплюнуть» даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

Наряду с этим, и обучаться устному счету лучше всего, используя для этого правильную и эффективную систему. С учетом этой системы и разработан наш курс, и сейчас будет логичным вкратце познакомить вас с содержанием его уроков.

Уроки устного счета

Уроки устного счета, представленные в нашем курсе, направлены именно на развитие трех вышеназванных составляющих. Вот их краткое описание:

Урок 1. Внимание и концентрация

Чтобы научиться считать в уме по-настоящему быстро, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Умение быть внимательным в нужный момент – этот навык, который выделяет великих ученых, спортсменов, политиков, несомненно, пригодится и вам.

Урок 2. Простые арифметические закономерности

Чтобы уметь решать сложные арифметические задачи, нужно для начала усвоить некоторые базовые закономерности. От того, как быстро вы сможете считать простейшие примеры, напрямую зависит ваше умение быстро выполнять более сложные математические операции. По сути, это можно считать базой для всего последующего обучения.

Урок 3. Традиционное умножение в уме

В этом уроке мы рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно, однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.

Урок 4. Частные методики умножения двузначных чисел до 30

Способы умножения двузначных чисел хороши тем, что они универсальны для любых чисел, и при хорошем навыке могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов. В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.

Урок 5. Опорное число при умножении чисел до 100

Наиболее популярной методикой умножения больших чисел в уме является прием использования так называемого опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100. В уроке вы познакомитесь с данной методикой и научитесь сами ее применять.

Урок 6. Умножение в уме любых чисел до 100

Чтобы умножать любые числа до 100 в уме, важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее эффективные случаи для каждой методики умножения. В уроке будут рассмотрены как универсальные методики (подходящие для любых чисел), так и частные (удобные для конкретных случаев).

Урок 7. Возведение в квадрат в уме

Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей. В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.

Также в нашем курсе представлены дополнительные материалы, помогающие тренировать и развивать умение считать устно:

Книги, учебники и ссылки на материалы по устному счету

К сожалению, в Интернете далеко не всегда удается найти качественные материалы, посвященные именно обучению счету в уме. Однако есть ряд интересных книг и сайтов, связанных с вопросами устного счета. С некоторыми из них вы и сможете познакомиться поближе, изучив данный раздел.

Дополнительные материалы по устному счету

Уместить в один курс всю важную и нужную информацию очень проблематично. Но она, несомненно, нужна, так что вы сможете углубить свои знания по рассматриваемой теме. В этом разделе вы найдете небольшую подборку полезных материалов (а именно эффективных обучающих программ и статей), которые помогут вам лучше изучить отдельные вопросы.

Далее предлагаем познакомиться с краткой инструкцией по прохождению курса.

Как проходить курс?

Уроки данного курса мы настоятельно рекомендуем проходить последовательно, не пропуская ни один из них, подробно рассматривая каждую тему и выполняя все практические указания. Лучше всего, если после изучения предлагаемых примеров вы будете придумывать несколько своих. Это позволит вам лучше понять и закрепить материал.

Если вам что-либо непонятно, перечитайте урок еще раз. Для более надежного закрепления материала в памяти советуем по окончании курса еще раз вернуться к наиболее сложным для вас темам. И, конечно же, по завершении обучения не примените возможностью познакомиться со всеми дополнительными материалами.

Цитаты известных людей о математике

Теперь же мы хотим, чтобы вы немного отдохнули перед основной работой. Ниже мы подобрали несколько цитат известных людей об умении считать. Пусть их слова станут для вас дополнительной мотивацией и еще раз напомнят о том, как важна математика:

Математика – это язык, на котором написана книга природы.

Галилео Галилей

Часто говорят, что цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется.

Иоганн Вольфганг фон Гете

В математике есть своя красота, как в живописи и поэзии.

Николай Жуковский

Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.

Алексей Крылов

Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.

Михаил Калинин

Первое условие, которое надлежит выполнять в математике, – это быть точным, второе – быть ясным и, насколько можно, простым.

Готфрид Лейбниц

Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на­стойчивость и упорство в достижении цели.

Алексей Маркушевич

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!

Дьердь Пойа

Счет и вычисления – основа порядка в голове.

Иоганн Генрих Песталоцци

Устройство нашего мира непостижимо без знания математики.

Роджер Бэкон

А сейчас вы можете проверить, насколько быстро вы считаете в уме:

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник