Установка лабораторная определение момента инерции тела динамическим способом

Установка лабораторная «Определение момента инерции тела динамическим методом». ФМ-22

Определение момента инерции тела динамическим методом . ФМ-22

НАЗНАЧЕНИЕ ИЗДЕЛИЯ

Установка лабораторная ФМ-22

Предназначена для проведения лабораторных работ курс «Физика», раздел «Механика», в высших учебных учреждениях.

Установка также может быть использована в колледжах, лицеях, техникумах, профтехучилищах.

ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ

Масса диска маховика, кг.: 630  5

Количество дополнительных грузов, штук: 4

Масса дополнительного груза, грамм: 200

Масса наборного груза, грамм: 150

Масса разновесов, грамм: 50

К оличество разновесов, штук: 3

Диаметр диска, мм 1 3 0

Диаметр расположения центров масс дополнительных

грузов на диске, мм 114

диаметр шкива с нитью, мм 40

Максимальное перемещение наборного груза, мм, 450

Габаритные размеры в сборе, мм,:

Точность измерения перемещения подвеса, мм. 1 — 0,5.

Питание установки сеть: 220В 50 Гц.

Потребляемая мощность , Вт 40

Установка «Маховик» обеспечивает возможность экспериментального определения момента инерции маховика и проверить справедливость теоремы Штайнера.

Наименование и условное обозначение

Источник

Лаб. раб. (методические указания) / Лабораторная работа №7 (Определение момента инерции тв. тела динам. методом)

Лабораторная работа №7

Определение момента инерции твердого тела с неподвижной осью динамическим методом.

Краткая теория.

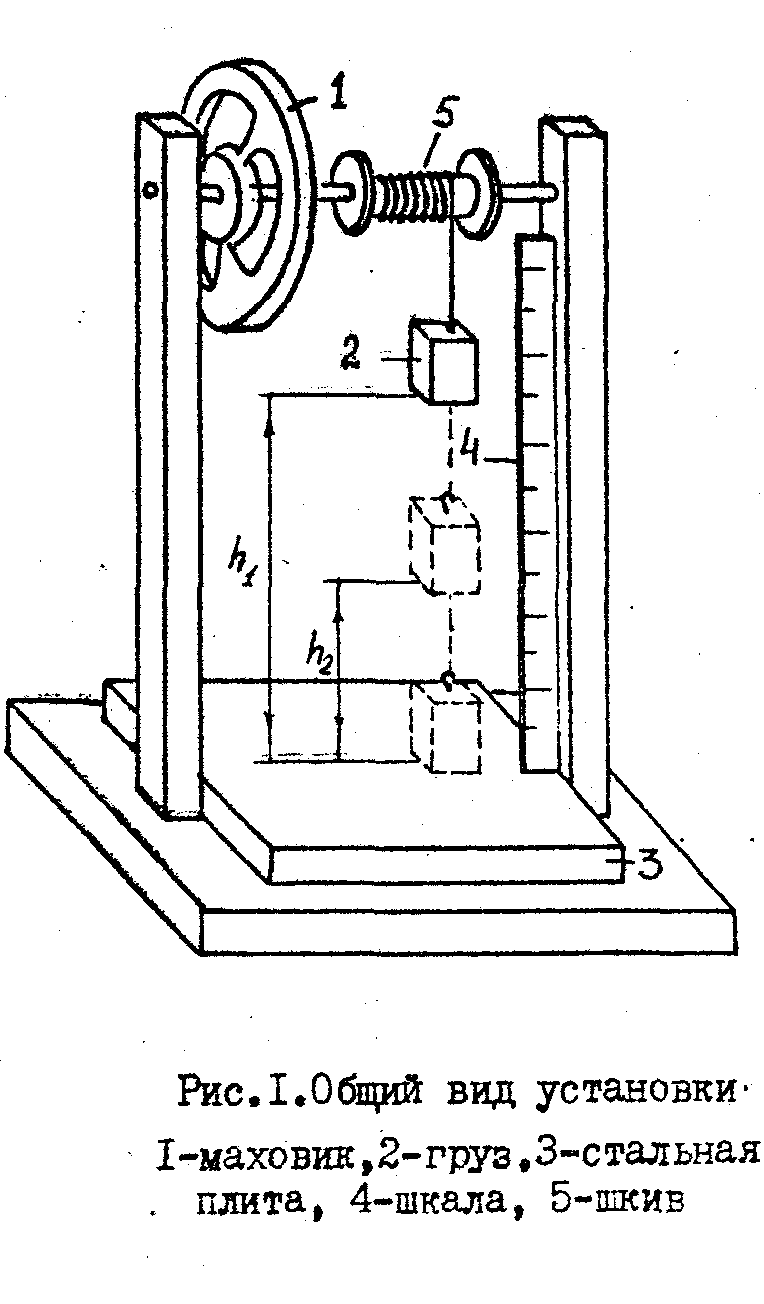
Целью данной работы является измерение момента инерции твердого тела сложной формы (маховика) относительно закреплённой оси вращения. Метод измерения основан на наблюдении совместного (связанного) движения двух тел: исследуемого маховика и груза, спускающегося на шнуре, который закреплён и намотан на шкиве вала маховика (см. рис. 1).

В таком движении вращающий момент, приводящий маховик во вращательное движение, создаётся действием момента силы натяжения F_н разматывающегося шнура и наличием некоторого трения в подшипниках за счет которого создается тормозящий момент сил трения М_тр. Уравнение движения вращающегося маховика согласно основному закону динамики вращательного движения твердого тела запишется равенством

(1)

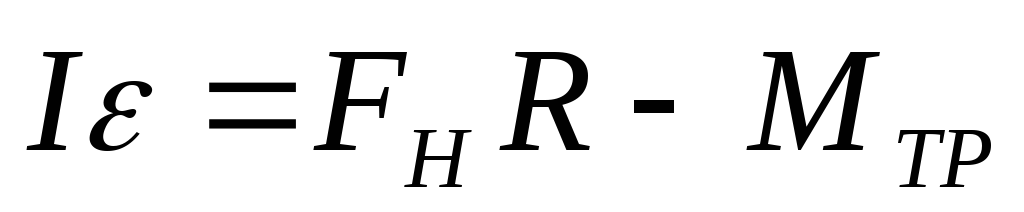
Здесь I – момент инерции маховика и деталей, вращающихся с ним (вал и шкив);  — угловое ускорение; R — радиус шкива.

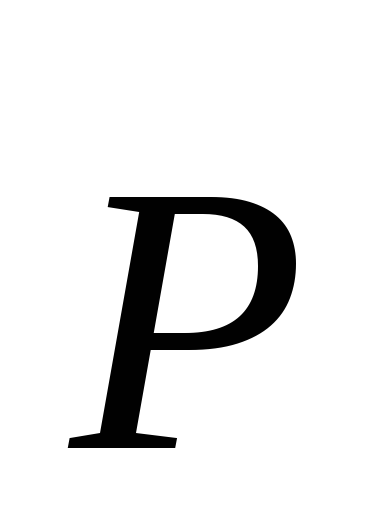
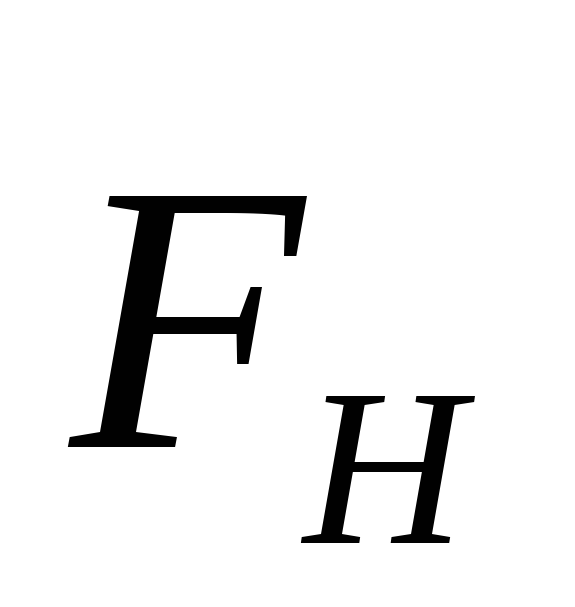
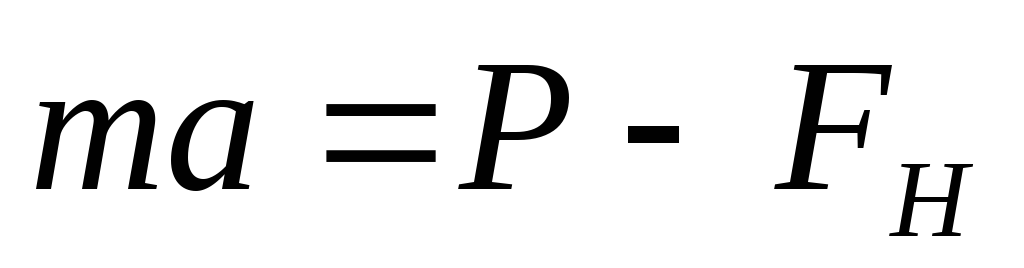
Движение груза совершается под действием двух противоположно направленных сил – веса и силы натяжения шнура .Считая направление вниз положительным и обозначив а ускорение, можем записать уравнением движения груза в виде

(2)

Из (2) выразим силу натяжения

(3)

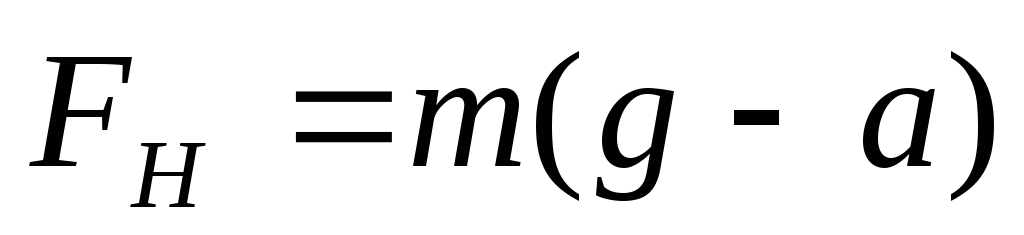
Подставляя найденную силу натяжения (3) в уравнение (1), получим

(4)

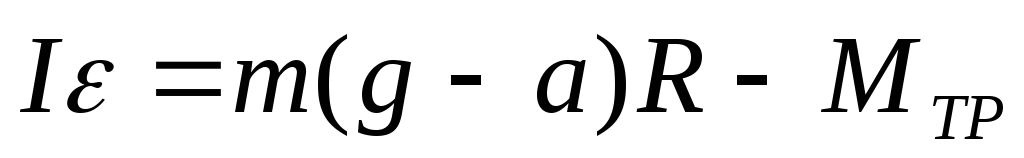
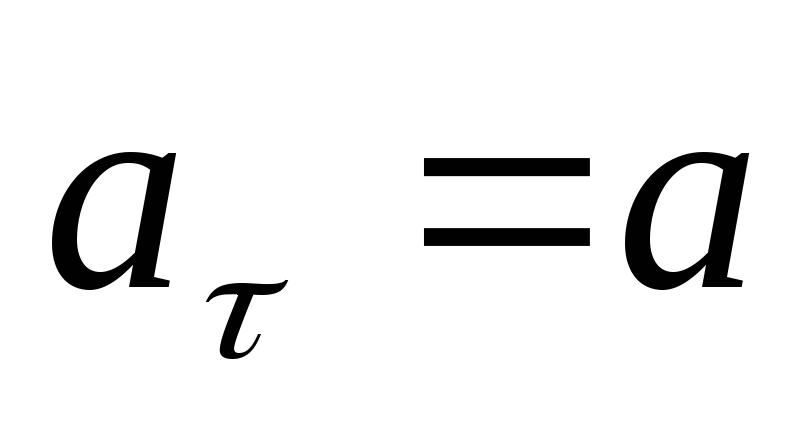
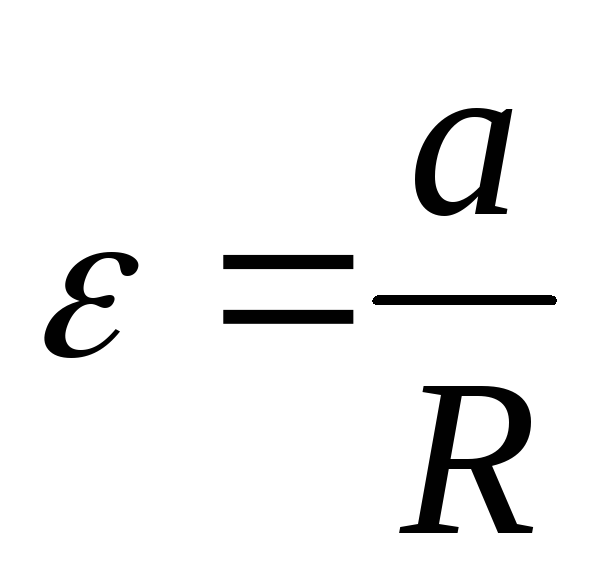
или так как линейное касательное ускорение точек поверхности шейки шкива, равное ускорению опускающегося груза , то

(5)

Уравнение (4) с учетом (5) перепишется так

(6)

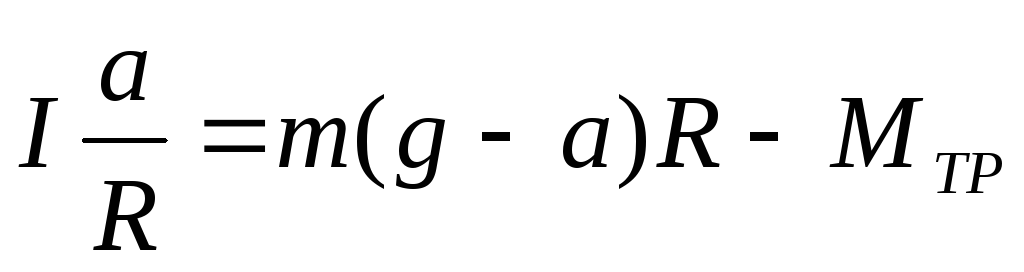
Из последнего равенства находим величину момента инерции

(7)

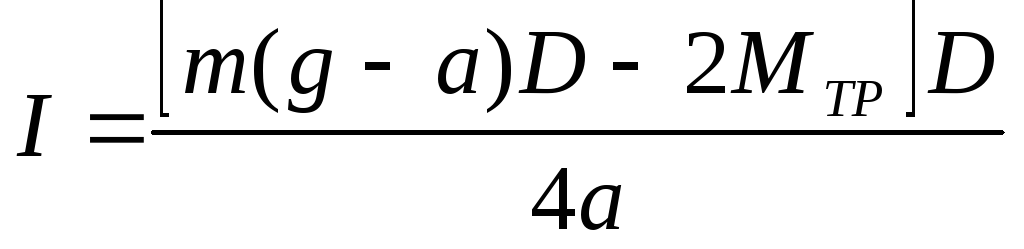
Так как в данной установке момент инерции вала и шкива ничтожно малы по сравнению с моментом инерции маховика, то уравнение (7) может рассматриваться как расчетная формула момента инерции маховика в предлагаемом методе измерения.

Как видно из (7), для нахождения момента инерции маховика, необходимо определить массу груза – m, диаметр шейки шкива D, ускорение движущегося груза а и момент сил трения в опорах М_тр. Масса m и диаметр шкива D определяются непосредственным измерением.

Ускорение а легко определить, измерив время опускания груза с известной высоты h₁ c начальной скоростью .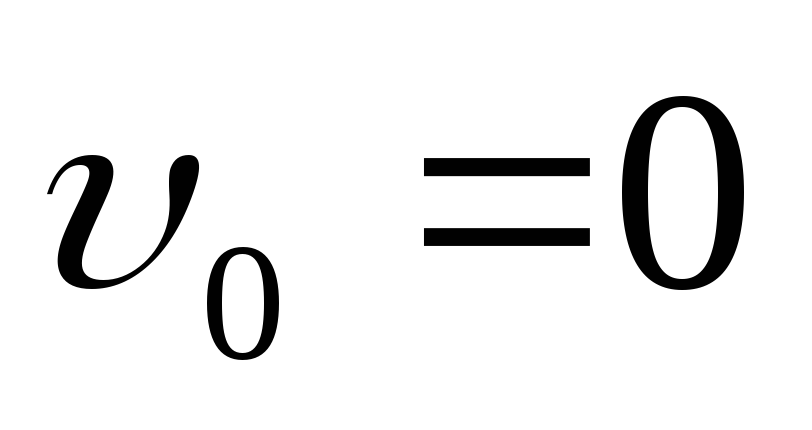

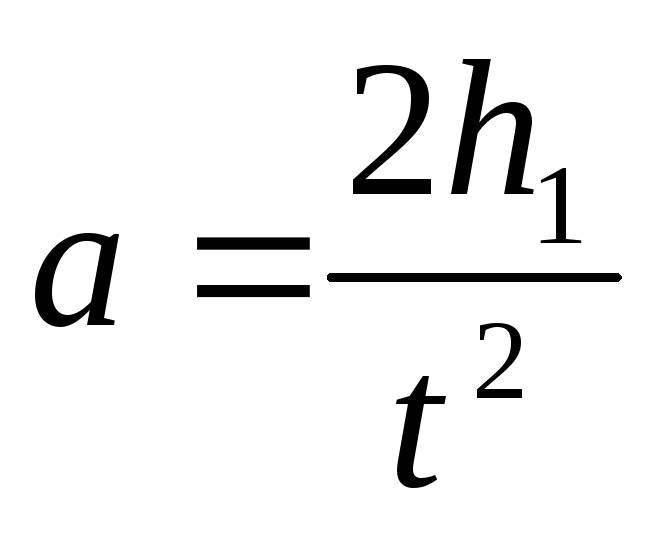
(8)

Момент сил трения в опорах можно вычислить исходя из следующих соображений. Допустим, что опустившись на полную длину шнура груз испытывает удар о неподвижное массивное основание (опору).Если считать удар вполне упругим, то скорость, приобретённая грузом, изменит свой знак, сохранив величину (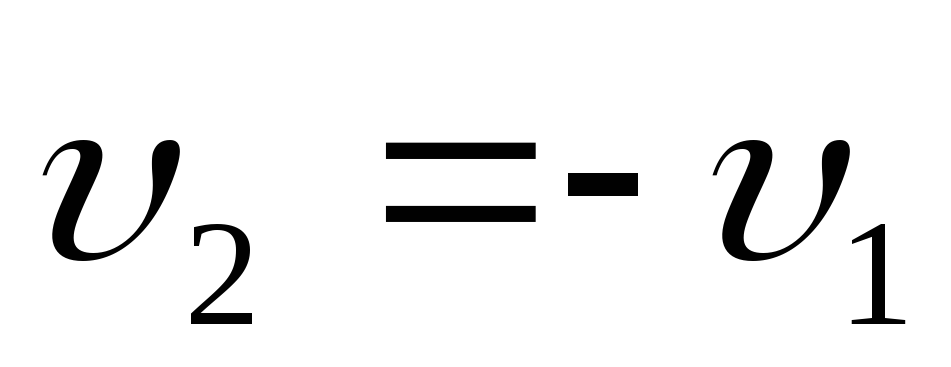). Груз начнет подниматься, а шнур будет наматываться на шкив в обратную сторону, так как маховик по инерции продолжает вращение в прежнем направлении. В результате груз поднимается на высоту h₂, меньшую h₁, так как часть энергии будет израсходована на совершение работы против сил трения.

По окончании рассмотренного движения, к моменту остановки маховика и груза, потенциальная энергия системы изменится на величину

(9)

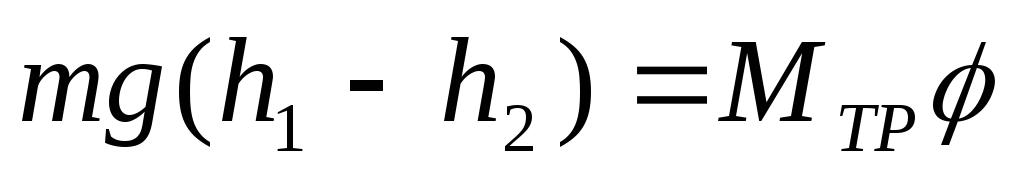
где  — общий угол поворота маховика (в радианной мере) за всё время его движения. Это угловое перемещение определяется очевидной формулой

(10)

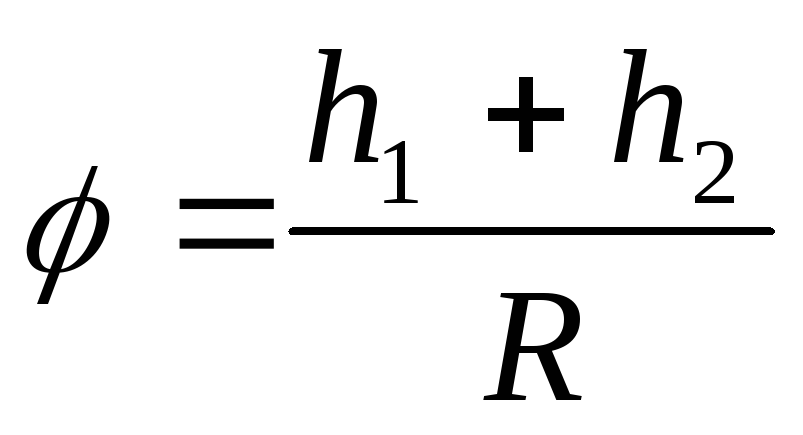
Исключая из равенства (9) и (10) угол  и решая их относительно момента силы трения, получим

(11)

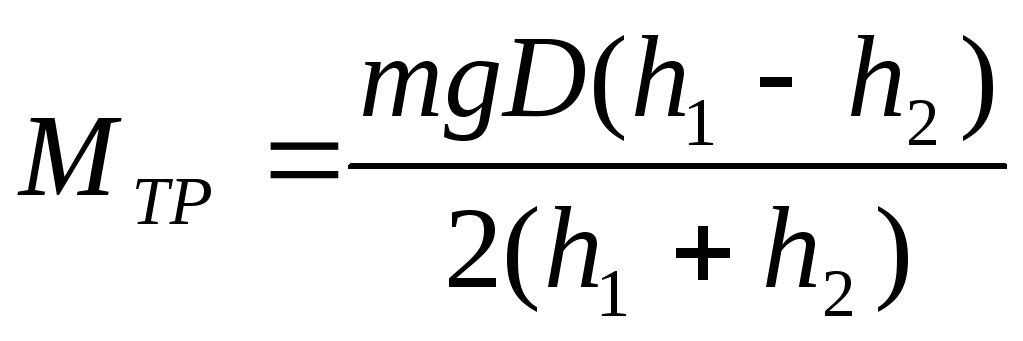
Подставляя (8) и (11) в (7) можно получить для расчёта момента инерции маховика выражение

(12)

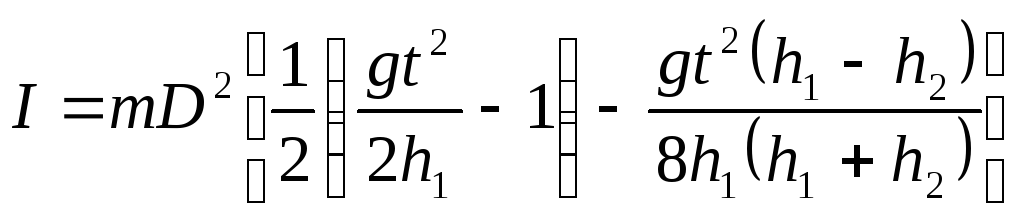
В процессе выполнения работы необходимо измерить высоту h₁ с которой без начальной скорости опущен груз, время t его спуска с этой высоты, и высоту h₂, на которую груз поднимается к моменту остановки маховика.

По результатам измерений вычисляются: момент сил трений М_тр формула (11) и момент инерции маховика I формула (12) или по формуле (7), вычислив предварительно ускорение а.

Порядок выполнения работы.

На подвижной платформе установить грузы общей массы около 0,8 – 1 кг. Вращая маховик, аккуратно намотать шнур подвеса на шкив с таким расчетом, чтобы основание платформы поднялось до выбранной начальной высоты h₁(0,6 – 0,8 м.) от опоры.

Измерить время спуска m груза до удара о массивную опору при помощи секундомера, повторив эту операцию 3 – 5 раз. Измерить высоту h₂ максимального подъёма груза. Результаты измерений занести в таблицу.

Время спуска t и высота подъёма h₂ груза при опускании с начальной высоты h₁.

Источник

Комплект учебно-лабораторного оборудования «Определение момента инерции тела динамическим способом»

УП6856

Лабораторный стенд «Определение момента инерции тела динамическим способом» выполнен в настольном модульном исполнении. Стенд состоит из массивного вала со шкивом, закрепленного на оси узла подшипников. На шкиве прикреплена нить с наборным грузом. На другом конце оси узла расположен диск, который служит для фиксации вращательной системы электромагнитным тормозом. Узел подшипников и электромагнитный тормоз закреплены на кронштейне, установленном на верхнем конце стойки с миллиметровой шкалой. Стойка закреплена на основании. Также на основании установлен фотодатчик. Кроме того, на стойке размещены два визира, которые могут перемещаться по всей длине стойки. Электропитание фотодатчика и электромагнитного тормоза, а также отсчет и индикация времени производятся с помощью электронного секундомера (электронного блока ФМ-1/1).

Лабораторный стенд «Определение момента инерции тела динамическим способом»

Электронный секундомер (электронный блок ФМ-1/1)

Комплект соединительных проводов

1. Лабораторный стенд «Определение момента инерции тела динамическим способом».
2. Комплект соединительных проводов.
3. Сетевой кабель.
4. Паспорт изделия.
5. Руководство по эксплуатации.
6. Методические рекомендации по выполнению лабораторных работ.

• Габариты: 300 х 400 х 1000 мм.
• Масса: не более 11 кг.
• Электропитание: 220 В, 50 Гц.
• Потребляемая мощность: 50 ВА.

Лабораторный стенд «Определение момента инерции тела динамическим способом» предназначен для изучения законов динамики вращательного движения твердого тела. Установка позволяет определять момент инерции тела динамическим методом.

Лабораторный стенд может применяться в процессе обучения в общеобразовательных учреждениях, учреждениях начального, среднего и высшего профессионального образования для получения базовых и углубленных профессиональных знаний и навыков по дисциплине «Физика: Механика. Вращательное движение».

Источник

ЛАБОРАТОРНАЯ РАБОТА 7 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА ДИНАМИЧЕСКИМ МЕТОДОМ

1 ЛАБОРАТОРНАЯ РАБОТА 7 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА ДИНАМИЧЕСКИМ МЕТОДОМ Краткая теория метода и описание установки Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат ее расстояния от оси вращения = m r (1) Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно В случае вращения тела вокруг любой неподвижной оси ОО тело разбивается на большое число весьма малых элементов с массами m i (рис1) Величина, численно равная сумме моментов инерции отдельных элементов, называется моментом инерции твердого тела относительно данной оси n i1 i i m r, () где r i расстояние i-того элемента до оси вращения, n число всех элементов, составляющих данное тело Вращательное движение характеризуется угловой скоростью () и угловым ускорением (), которые определяются по формулам: d d,, (3) где — угловое перемещение тела Законы вращательного движения (t) и (t) аналогичны законам S (t) и U (t) для поступательного движения Например, = t закон равномерного вращения, t 0t, и 0 t — законы равноускоренного движения с начальной угловой скоростью Связь между линейной и угловой скоростями, линейным и угловым ускорением следующая: U = r, (4) a = r, (5) где r расстояние точек до оси вращения 3

2 Основной закон динамики вращательного движения выражается формулой M, (6) где — угловое ускорение, момент инерции тела относительно данной оси, M суммарный момент действующих на тело сил 1 Кинетическая энергия вращающегося тела определяется по формуле: E вр k, (7) где — угловая скорость вращения, момент инерции тела Сопоставляя формулы для вращательного движения (6) и (7) с соответствующими закономерностями для поступательного движения (второй закон Ньютона, кинетическая энергия поступательного движения) можно сделать вывод, что момент инерции тела () во вращательном движении выполняет ту же роль что и масса тела в поступательном движении Таким образом, если масса служит мерой инертности тела в поступательном движении, то во вращательном движении мерой инертности является момент инерции тела () Для тел правильной геометрической формы момент инерции может быть рассчитан теоретически Для тел произвольной сложной формы момент инерции определяется опытным путем Одним из возможных способов определения момента инерции является динамический метод Схема установки для определения момента инерции динамическим методом изображена на рис 1 Моментом силы относительно неподвижной оси называется величина, численно равная произведению величины силы на ее плечо, те расстояние от оси вращения до прямой, вдоль которой действует сила 4

3 Прибор состоит из шкива h, радиуса r, закрепленного на оси О, четырех стержней, расположенных под углом 90 0 друг к другу, и четырех одинаковых грузов m 1, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси Грузы закрепляются симметрично, те так, чтобы центр тяжести системы совпал с осью вращения Прибор приводится во вращательное движение при падении груза массой m, прикрепленного к концу шнура, который намотан на шкив h (см рис) На движущийся поступательно вниз груз m будет действовать две силы: P — сила тяжести, F н — сила натяжения шнура (см рис) Под действием сил груз m будет двигаться вниз равноускоренно (с линейным ускорением а) На шкив со стержнем и закрепленными на них грузами действует сила натяжения нити F н (рис), создающая вращающий момент M F н r Под действием этого постоянного момента силы система «шкив с крестовиной», согласно (6), будет вращаться равноускоренно (с постоянным ускорением ) Груз m, поднятый над полом на высоту h, обладает запасом потенциальной энергии E п mgh Если груз m начинает опускаться, то потенциальная энергия будет переходить в кинетическую энергию вращающейся крестовины с грузами E к вр и кинетическую энергию m U поступательно движущегося тела m: Eк пост Пренебрегая силами трения и сопротивления в системе, на основании закона сохранения механической энергии можно записать 5

4 m U mgh (8) Так как шнур намотан на вал, то линейная скорость точек на поверхности вала равна скорости поступательного движения груза m, те U = r (9) Груз m движется вниз равноускоренно без начальной скорости, следовательно, для его движения справедливы следующие законы at h (10) U at (11) С помощью формул (9), (10), (11) уравнение (8) можно преобразовать относительно момента инерции к виду: mr ( gt h ) h (1) Принимая во внимание, что r = D/, где D диаметр вала, на который намотан шнур, формула (1) принимает вид: md ( gt h ) 8h (13) ХОД РАБОТЫ Приборы и принадлежности: лабораторная установка для определения момента инерции динамическим методом, масштабная линейка, секундомер, штангенциркуль 1 С помощью штангенциркуля измерить диаметр вала, к которому прикреплен шнур с грузом Измерения следует проводить в различных участках вала Вращая вал с крестовиной, поднять груз на высоту h и измерить с помощью масштабной линейки высоту поднятия груза над уровнем пола (отсчитывается расстояние от пола до нижнего основания груза) 3 Предоставить грузу возможность падать, по секундомеру определить промежуток времени, в течение которого груз опускается до пола 4 Результаты измерений и расчетов занести в таблицу: опыта m m h h D D t t 6

5 5 Определить момент инерции по формуле (13), подставляя средние значения всех измеряемых величин в системе СИ 6 Исходя из расчетной формулы (13), вывести формулу для подсчета относительной ошибки 7 Подсчитать численные значения относительной и абсолютной погрешностей и записать окончательный результат в виде: ист ср ср КОНТРОЛЬНЫЕ ВОПРОСЫ: 1 Какая величина называется моментом инерции материальной точки? Твердого тела? От чего зависит момент инерции тела? Какой физический закон лежит в основе вывода расчетной формулы? Определить границы его применимости 3 Определить вид движения и записать законы движения падающего груза 4 Определить вид движения и записать законы движения для вращающейся части системы 5 Какая существует связь между линейными и угловыми характеристиками при вращательном движении? ЛИТЕРАТУРА 1 Яворский БМ, Детлаф АА Курс общей физики т I М, 1975 Савельев ИВ Курс общей физики т I М, Зисман ГА, Тодес ОМ Курс общей физики т I М, Кортнев АВ, Рублев ЮВ, Куценко АН Практикум по физике (теория погрешностей стр 15-30) 7

6 ЛАБОРАТОРНАЯ РАБОТА 15 ОПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ ДЛИНЫ И МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА Кинематика гармонических колебаний Колебательным движением называется всякое движение или изменение состояния, характеризуемое той или иной степенью повторяемости во времени значений физической величины, определяющей это движение или состояние Колебательное движение называется периодическим, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени Простейшим видом периодических колебаний являются гармонические колебания Колебания какой-либо величины называются гармоническими, если ее зависимость от времени t имеет вид: x = A sin (t + 0 ) (1) или x = A cos (t + 0 ), () причем A, с течением времени не изменяются x смещение колеблющейся величины или материальной точки от положения равновесия; A амплитуда колебаний наибольшее смещение; t + 0 фаза колебаний физическая величина, определяющая смещение колеблющейся точки в данный момент времени; 0 начальная фаза колебаний, те при t = 0 фаза колебаний равна 0 ; — круговая или циклическая частота колеблющейся точки Если фаза колебания увеличивается или уменьшается на, то x примет прежнее значение, те, если x 1 = A sin (t ) и x = A sin (t + 0 ), x 1 = x, или A sin (t ) = A sin (t + 0 ), тогда t + 0 (t ) = Отсюда (t t 1 ) = ; t t 1 наименьшее время, по истечении которого повторяются значения всех физических величин, характеризующих колебание Это время названо периодом колебаний Т За время Т совершается одно полное колебание Следовательно, Т =,, (3) T но 8

7 1 T, (4) где — частота колебаний число полных колебаний, совершаемых за единицу времени Сравнивая формулы (3) и (4), получим = Таким образом, циклическая частота численно равна числу колебаний, совершаемых за секунд При гармонических колебаниях гармонически колеблется не только dx du смещение x, но и скорость, и ускорение Учитывая, что U, а a, продифференцировав x, получим выражение для U dx U Acos( t 0 ), (5) и, продифференцировав U, получим выражение для а: a A sin( t 0 ) 0 x (6) А — амплитуда скорости; А амплитуда ускорения Динамика гармонических колебаний По второму закону Ньютона сила, вызывающая гармонические колебания, равна F ma (7) Сравнивая формулы (6) и (7), получим F m Asin( t 0 ) m x (8) Сила, действующая на колеблющуюся точку, прямо пропорциональна смещению и всегда направлена к положению равновесия, поэтому ее часто называют возвращающей силой Примером сил, удовлетворяющих уравнению (8), являются упругие силы Силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие условию (8), называются квазиупругими: F1 kx (9) где k = m коэффициент квазиупругой силы Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси О, не проходящей через ее центр тяжести На рис1 изображено сечение физического маятника плоскостью, перпендикулярной к его оси вращения О и проходящей через его центр масс С Расстояние ОС равно а На рис1 F 1 и F 9

8 — составляющие силы тяжести mg F 1 — возвращающая сила При малых F 1 mgsin mg Знак минус указывает, что сила направлена против направления смещения Величина возвращающей силы в данном примере является частным случаем квазиупругой силы F1 kx При малых углах отклонения, колебания физического маятника являются гармоническими Возвращающий момент, создаваемый силой F 1, равен: M mga Основное уравнение динамики для маятника запишется следующим образом: d M, M, где момент инерции маятника; — угловое ускорение d mga, или d mga 0 Решениями этого дифференциального уравнения являются mga 0 sin( t 0 ),, но, T отсюда T mga Период малых колебаний физического маятника можно определить по формуле T mga Математический маятник Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити На рис видим, что возвращающая сила F 1 является одной из составляющих силы тяжести и равна x F1 mgsin mg sin, при малых l x F1 mg, те вновь видим, что F 1 — l квазиупругая сила, те при малых углах 10

9 отклонения колебания математического маятника являются гармоническими d x По второму закону Ньютона F1 ma, но a, тогда d x x m mg 0 l Решениями этого дифференциального уравнения являются g x = A sin (t + 0 ), Учитывая, что, получим, что период l T колебаний математического маятника равен l T g (11) Формулу (11) можно получить из формулы (10), если рассматривать математический маятник как частный случай физического, у которого вся масса сосредоточена в центре масс С на расстоянии а от подвеса, равном длине l нити математического маятника Тогда = m l, из формулы (10) следует формула (11) Приведенной длиной физического маятника называется длина такого математического маятника, который колеблется синхронно с физическим, те имеет равный с ним период колебаний Сравнивая формулы (10) и (11), получим l L, ma где а — приведенная длина физического маятника Тогда для физического маятника можно записать L T g Если физический маятник совершит N колебаний за секунд, а математический маятник n колебаний за t секунд, тогда получим L (1) N g t n l (13) g Решая совместно уравнения (1) и (13), получим 11

10 Если n = N, = t, то и L = l n r L l (14) N t ХОД РАБОТЫ 1 Измерить длину математического маятника l Измерить время n = 0 полных колебаний t математического маятника (3 раза) 3 Измерить время 0 полных колебаний физического маятника (3 раза) 4 Подсчитать приведенную длину физического маятника по формуле (14) n ср L l N t 5 Вычислить погрешности L и L L L ср 6 Определить положение центра тяжести физического маятника Для этого подвесить маятник поочередно в двух точках подвеса Провести через точки подвеса вертикальные линии Точка пересечения этих линий и есть центр тяжести тела Измерить расстояние от точки подвеса физического маятника до центра тяжести 7 Вычислить момент инерции физического маятника по формуле ma ср L ср 8 Вычислить погрешности и 9 Написать ответы: Lср Lср, ср ср Таблица 1 l l n t t N L 1

11 m m a a Таблица КОНТРОЛЬНЫЕ ВОПРОСЫ 1 Что называется гармоническим колебанием? Какой маятник называется физическим? Математическим? 3 Что называется приведенной длиной физического маятника? 4 Как определяется период колебаний физического и математического маятников? 5 Что такое циклическая частота колебаний? Как она связана с периодом и частотой? 6 Как рассчитать скорость и ускорение гармонически колеблющейся точки? 7 Как рассчитать кинетическую, потенциальную энергию гармонически колеблющейся точки? ЛИТЕРАТУРА 1 Яворский БМ, Детлаф АА Курс общей физики т I М, 1975 Савельев ИВ Курс общей физики т I М, Зисман ГА, Тодес ОМ Курс общей физики т I М,

Источник