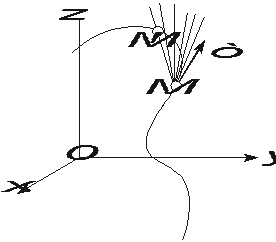
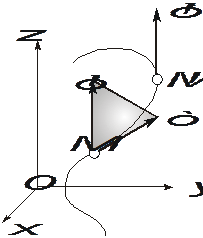
Ускорение точки
Скорость точки.
Перейдем к решению второй основной задачи кинематики точки — определению скорости и ускорения по уже заданному векторным, координатным или естественным способом движению.
1. Скоростью точки называется векторная величина, характеризующая быстроту и направление перемещения точки. В системе СИ скорость измеряется в м/с.
a) Определение скорости при векторном способе задания движения.
Пусть движение точки задано векторным способом, т.е. известно векторное уравнение (2.1):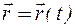 
.
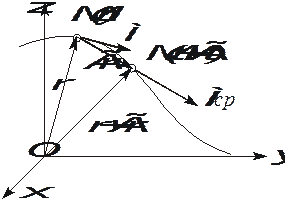
Рис. 2.6. К определению скорости точки
Пусть за время Dt радиус-вектор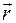 
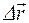
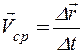
точки М изменится на величину 
. Тогда средней скоростью точки М за время Dt называется векторная величина
.
Мгновенной скоростью (или далее — просто скоростью) называется предел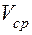 
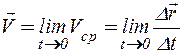
при Dt стремящемся к нулю, т.е.
. (2.4)
Вспоминая определение производной, заключаем:
. (2.5)
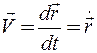
Здесь и в дальнейшем знаком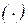 
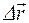
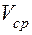
будем обозначать дифференцирование по времени. При стремлении Dt к нулю вектор , а, следовательно, и вектор , поворачиваются вокруг точки М и в пределе совпадают с касательной к траектории в этой точке. Таким образом, вектор скорости равен первой производной от радиус-вектора по времени и всегда направлен по касательной к траектории движения точки.
б) Скорость точки при координатном способе задания движения.
Выведем формулы для определения скорости при координатном способе задания движения. В соответствии с выражением (2.5), имеем:
.
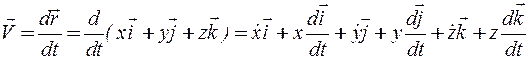
Так как производные от постоянных по величине и направлению единичных векторов равны нулю, получаем
. (2.6)
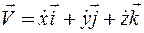
Вектор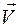 
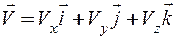
, как и любой вектор, может быть выражен через свои проекции:
(2.7)
Сравнивая выражения (2.6) и (2.7) видим, что производные координат по времени имеют вполне определенный геометрический смысл — они являются проекциями вектора скорости на координатные оси. Зная проекции, легко вычислить модуль и направление вектора скорости (рис. 2.7):
или 
, (2.8)
, 
, 
. (2.9)
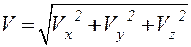
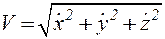
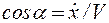
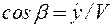
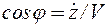
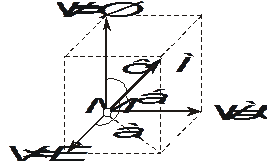
Рис. 2.7.К определению величины и направления скорости
в) Определение скорости при естественном способе задания движения.
Рис. 2.8. Cкорость точки при естественном способе задания движения
Согласно (2.4)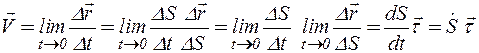 
,
где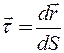 
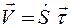
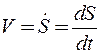
— единичный вектор касательной. Таким образом,
, 
(2.10)
Величина V=dS/dt называется алгебраической скоростью. Если dS/dt>0, то функция S = S(t) возрастает и точка движется в сторону увеличения дуговой координаты S, т.е. точка движется в положительном направлении Если же dS/dt 2 .
a) Определение ускорения при векторном способе задания движения.
Пусть точка М в момент времени t находится в положении М(t) и имеет скорость V(t), а в момент времени t + Dt находится в положении М(t + Dt) и имеет скорость V(t + Dt) (см. рис. 2.9).
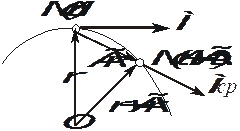
Рис. 2.9. Ускорения точки при векторном способе задания движения
Средним ускорением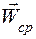 
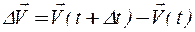
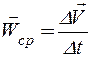
за промежуток времени Dt называется отношение изменения скорости 
к Dt , т.е.
.
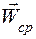
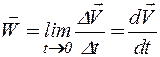
Предел при Dt ® 0 называется мгновенным (или просто ускорением) точки М в момент времени t
. (2.11)
Согласно (2.11), ускорение при векторном способе задания движения равно векторной производной от скорости по времени.
б). Ускорения при координатном способе задания движения.
Подставляя (2.6) в (2.11) и дифференцируя произведения в скобках, находим:
.
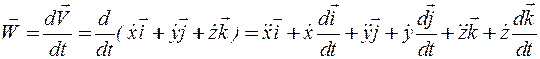
Учитывая, что производные от единичных векторов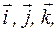 
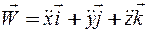
равны нулю, получаем:
. (2.12)
Вектор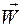 
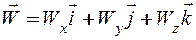
может быть выражен через свои проекции:
. (2.13)
Сравнение (2.12) и (2.13) показывает, что вторые производные от координат по времени имеют вполне определенный геометрический смысл: они равны проекциям полного ускорения на координатные оси, т.e.
, 
, 
.
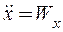
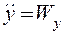
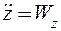
Зная проекции, легко вычислить модуль полного ускорения и направляющие косинусы, определяющие его направление:
, 
, 
, 
. (2.14)
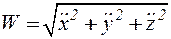
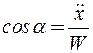
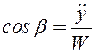
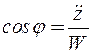
в). Ускорение точки при естественном способе задания движения
Приведем некоторые сведения из дифференциальной геометрии, необходимые для определения ускорения при естественном способе задания движения.
Пусть точка М движется по некоторой пространственной кривой. С каждой точкой этой кривой связаны три взаимно ортогональные направления (касательная, нормаль и бинормаль), однозначно характеризующие пространственную ориентацию бесконечно малого элемента кривой вблизи данной точки. Ниже приводится описание процесса определения указанных направлений.
Для того чтобы провести касательную к кривой в точке М , проведем через нее и близлежащую точку М1 секущую ММ1.
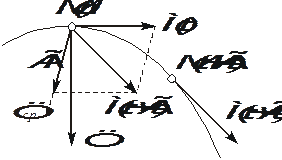
Рис. 2.10. Определение касательной к траектории движения точки
Касательная к кривой в точке М определяется как предельное положение секущей ММ1 при стремлении точки М1 к точке М (рис. 2.10). Единичный вектор касательной принято обозначать греческой буквой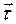 
.
Проведем единичные векторы касательных к траектории в точках М и М1. Перенесем вектор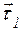 
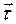
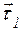
в точку М (рис. 2.11) и образуем плоскость, проходящую через эту точку и векторы и . Повторяя процесс образования аналогичных плоскостей при стремлении точки М1 к точке М, мы получаем в пределе плоскость, называемую соприкасающейся плоскостью.
Рис. 2.11. Определение соприкасающейся плоскости
Очевидно, что для плоской кривой соприкасающаяся плоскость совпадает с плоскостью, в которой лежит сама эта кривая. Плоскость, проходящая через точку М и перпендикулярная касательной в этой точке, называется нормальной плоскостью. Пересечение соприкасающейся и нормальной плоскостей образует прямую, называемую главной нормалью(рис. 2.12).
Источник
Векторный способ задания движения точки
Введение
Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.
При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.
Нормальное ускорение
Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 06-03-2016 Изменено: 29-01-2020
Источник
