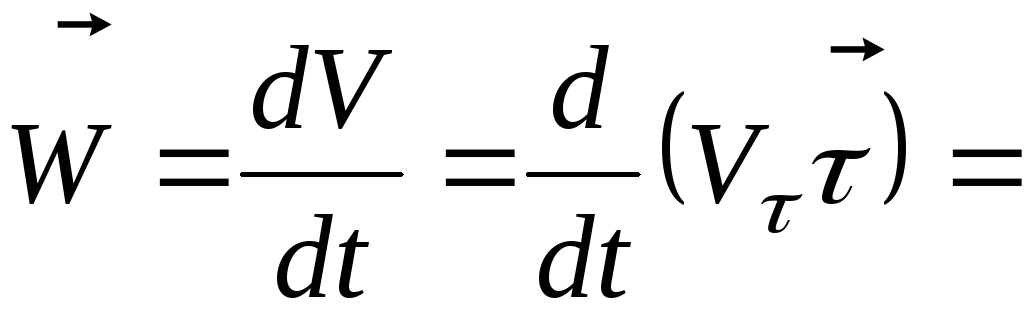1.1.3. Ускорение точки при векторном и координатном способах задания движения


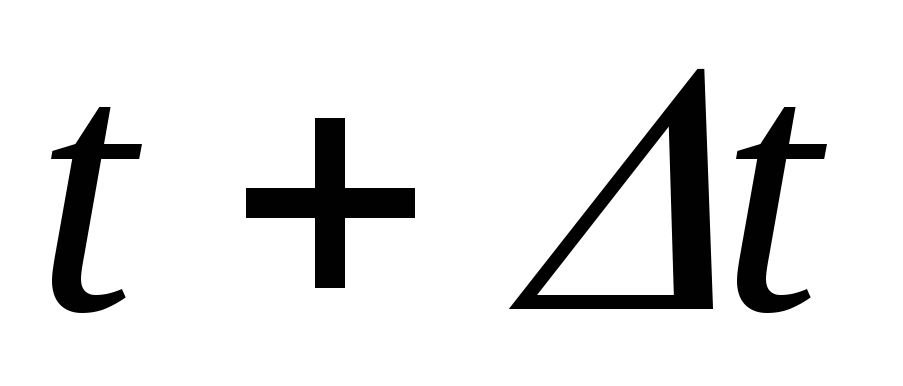
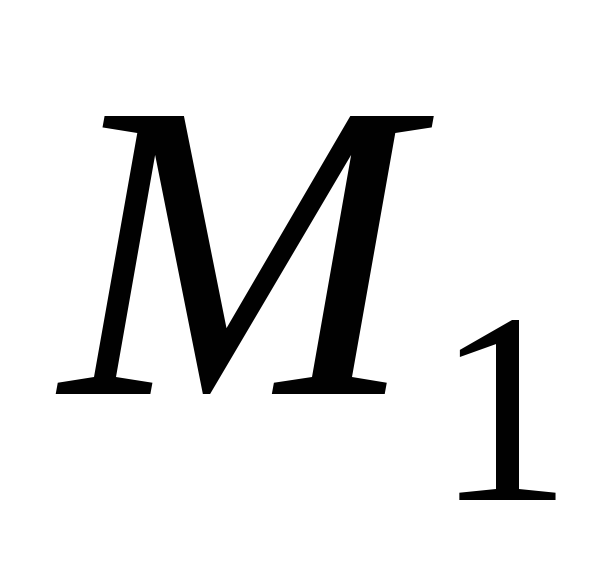






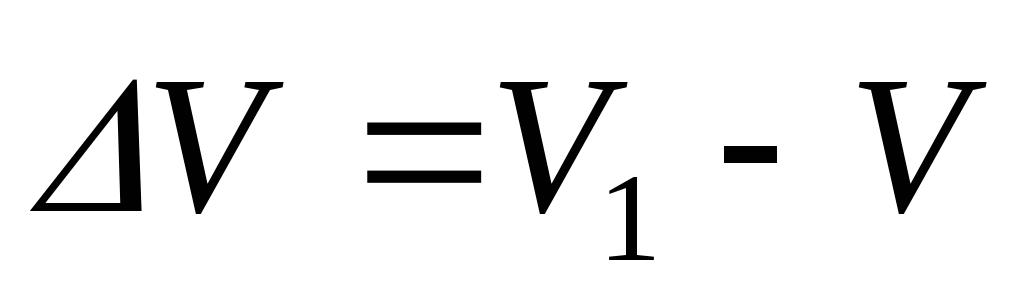
т. е. приращение вектора 



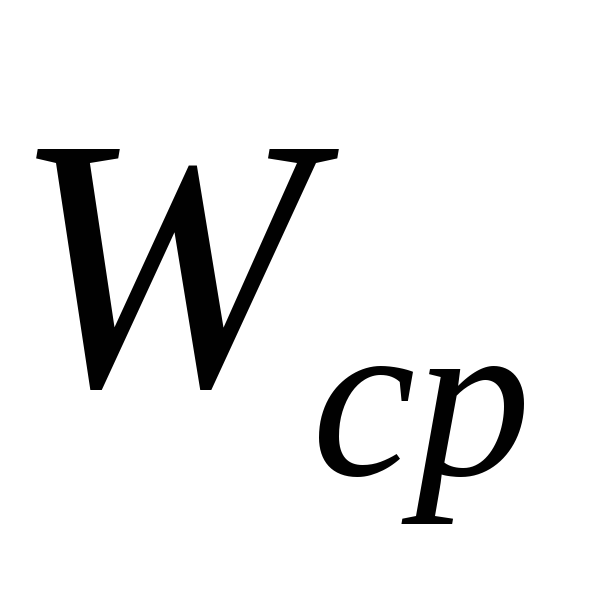

Ускорением точки в данный момент времени называется вектор 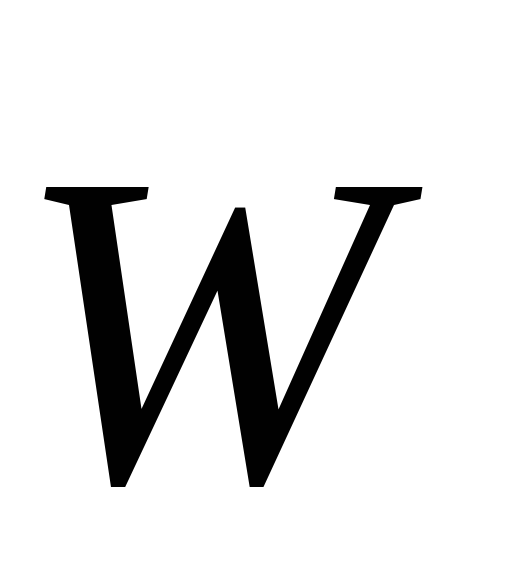
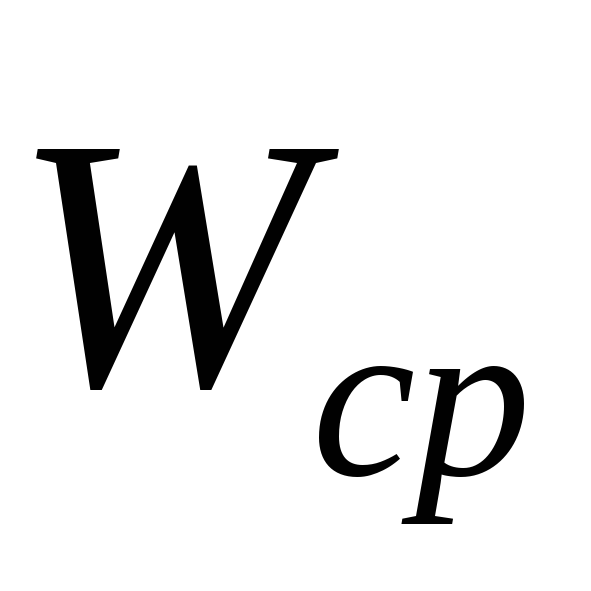
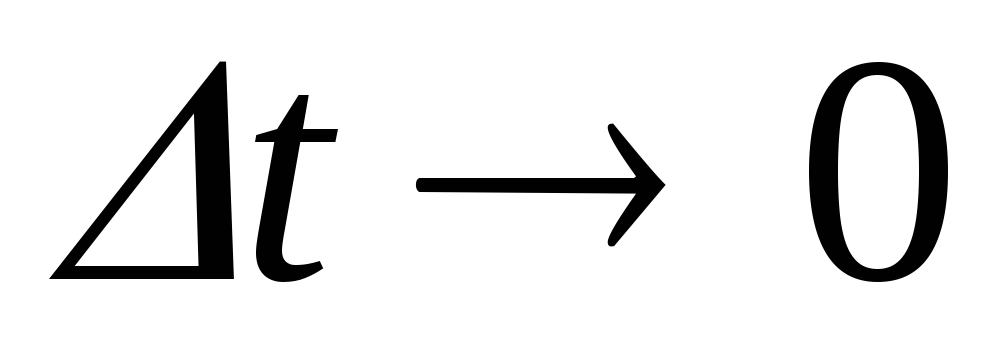
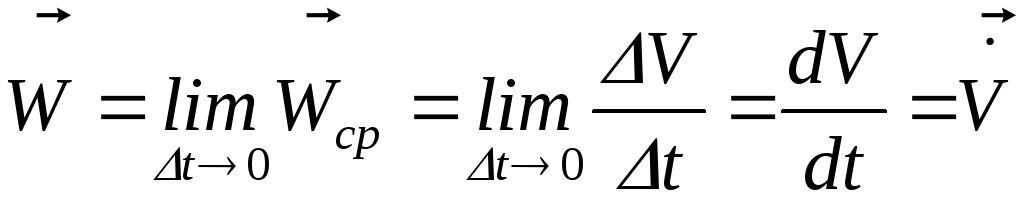
Учитывая формулу (1.1.8), можно записать
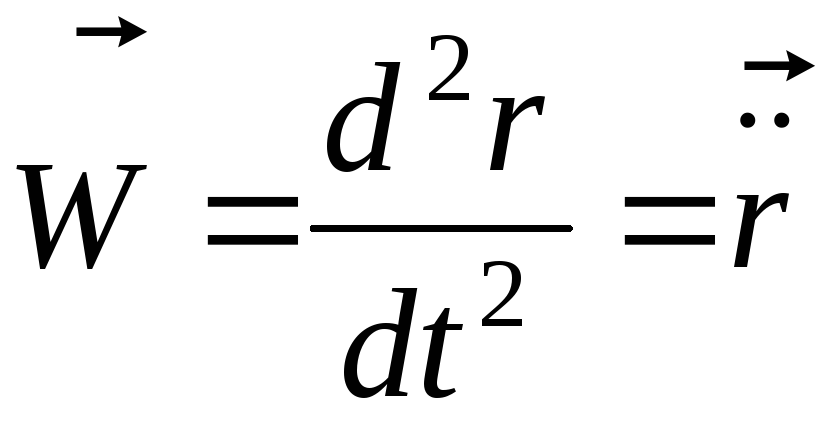
Ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиус-вектора точки.
Ускорение точки при координатном способе задания движения
Пусть движение точки задается уравнениями (1.1.2). Формулу (1.1.20) с учетом зависимости (1.1.11) можно представить в следующем виде: 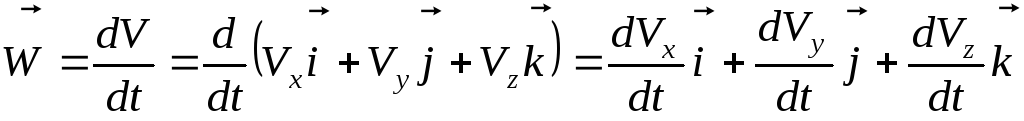
где 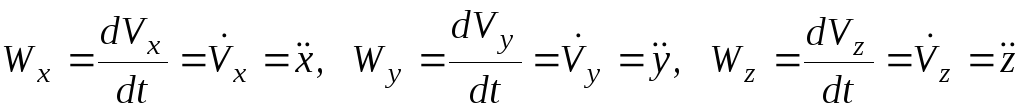
проекции ускорения точки на неподвижные оси декартовых координат.
Следовательно, проекции ускорения точки на неподвижные оси декартовых координат равны первым производным по времени от соответствующих проекций скоростей или вторым производным по времени от соответствующих координат.
Модуль ускорения точки равен
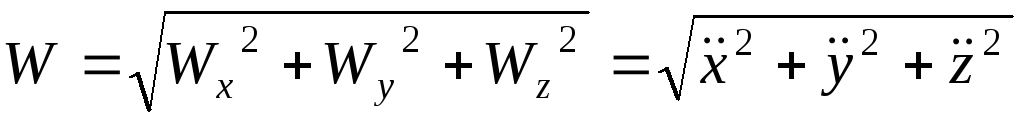
а направление вектора 
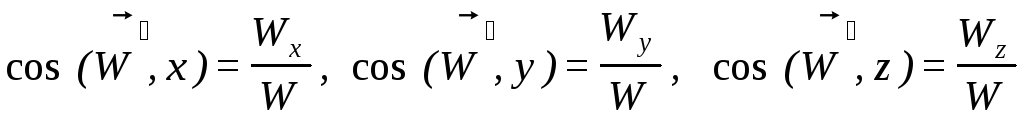
1.1.4. Ускорение точки при естественном способе задания движения
При естественном способе задания движения с точкой М связывают сис-тему отсчёта, представляющую собой оси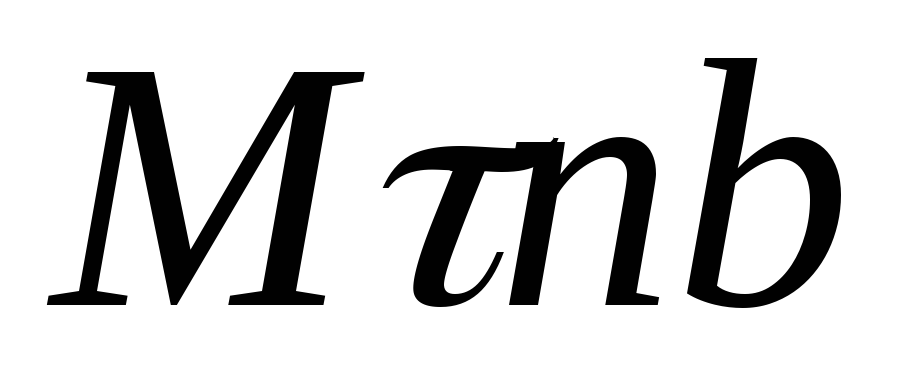
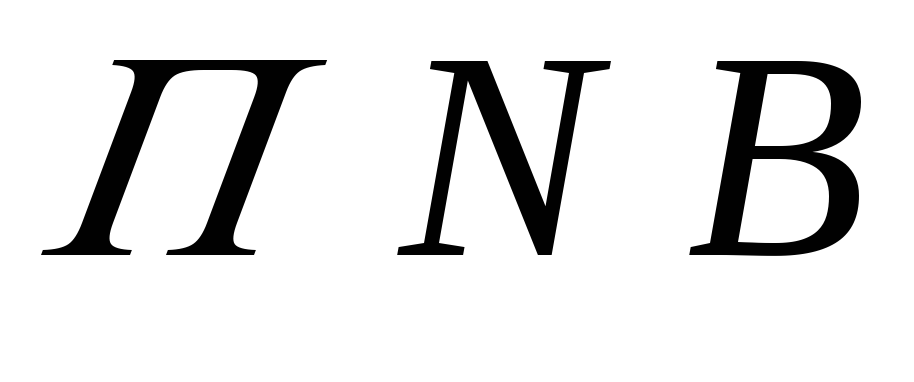
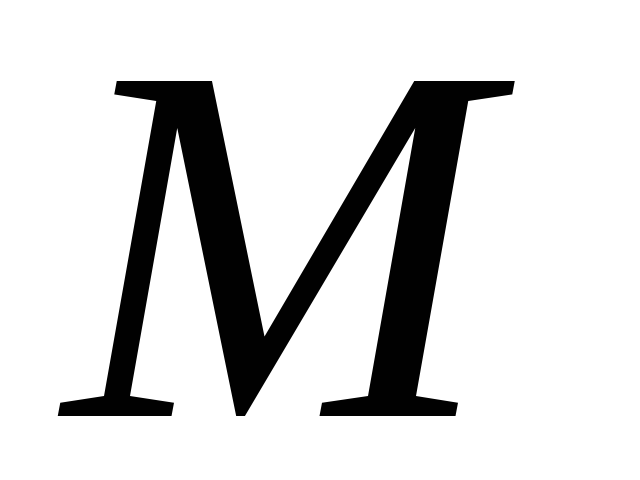
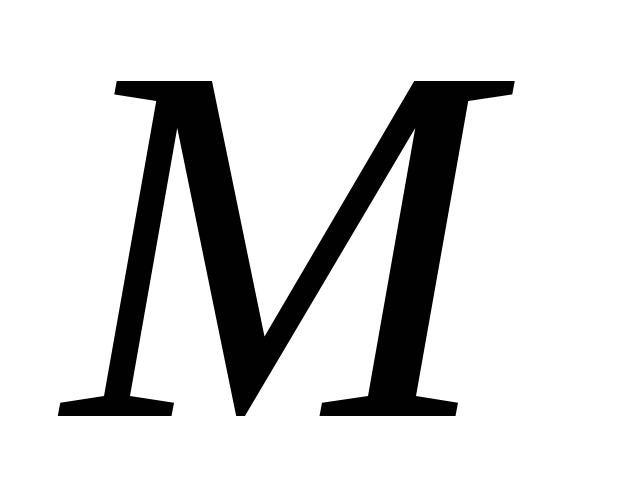
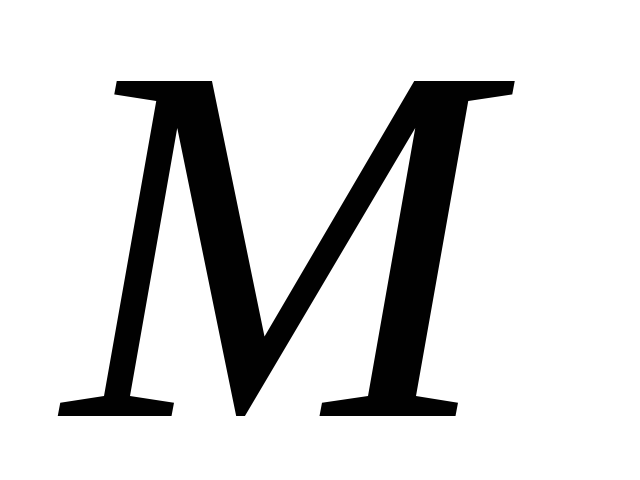
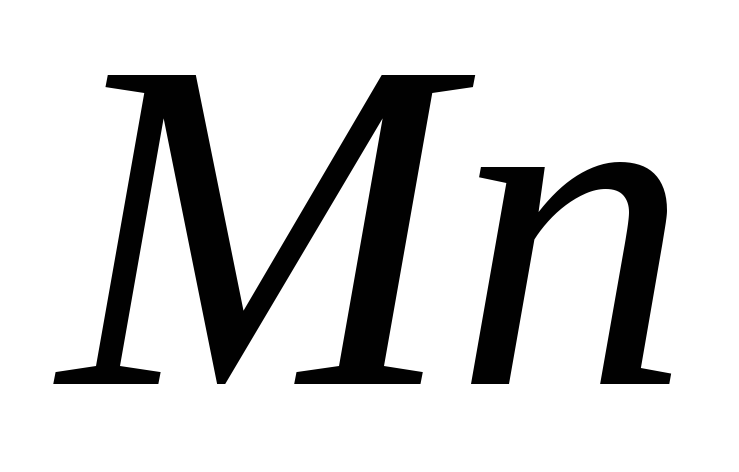
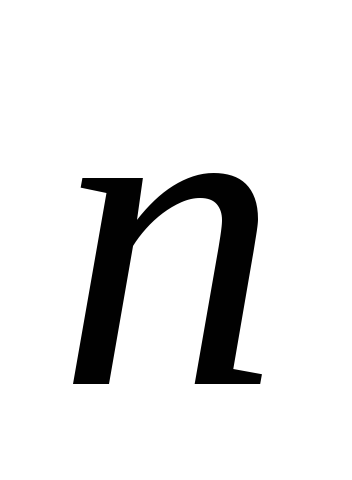
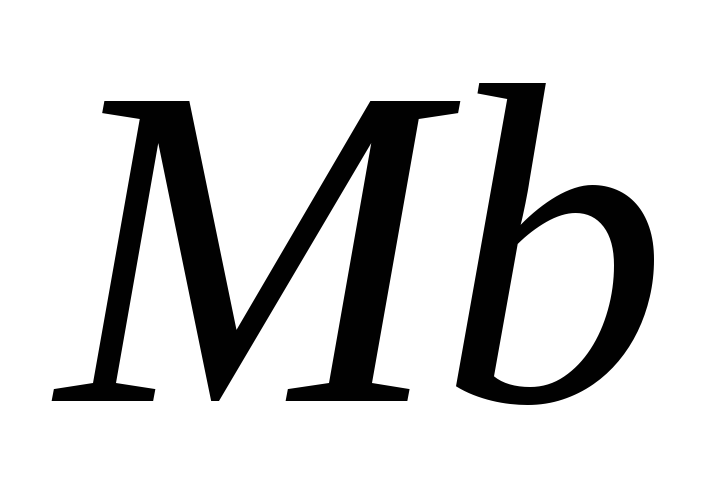
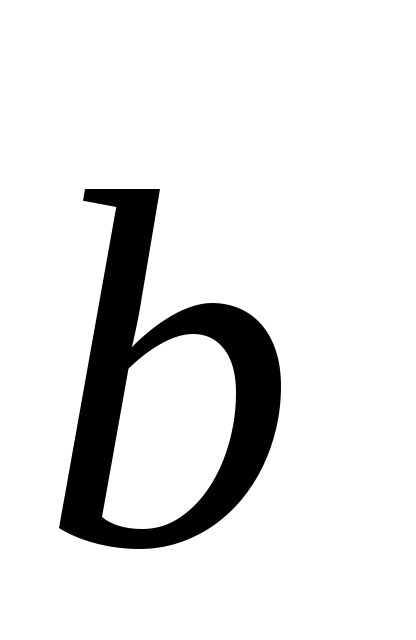
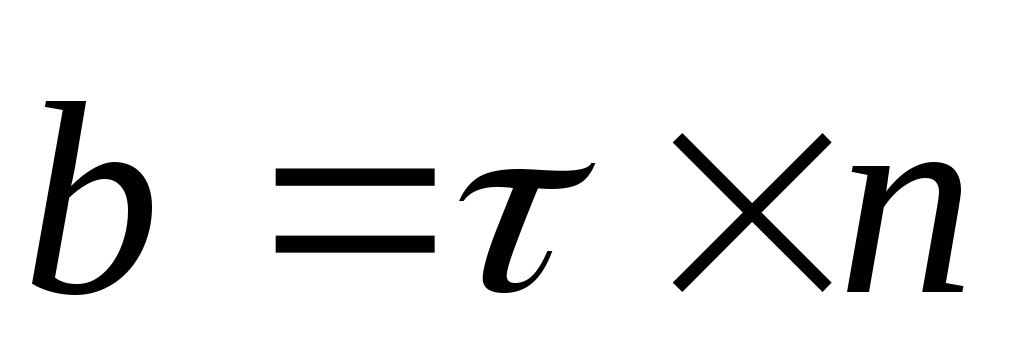

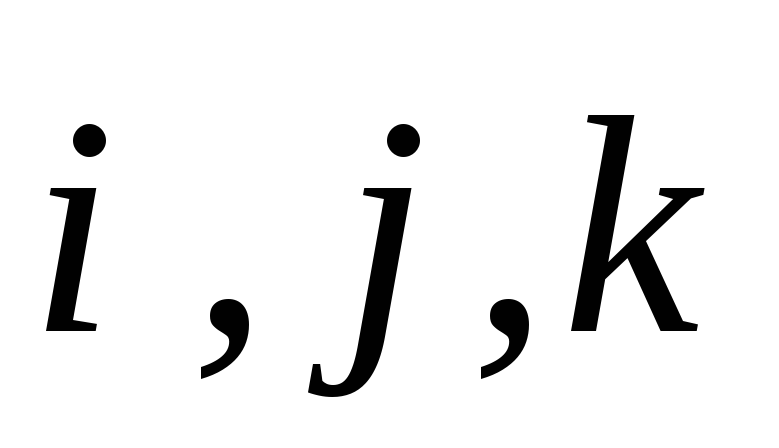

Т
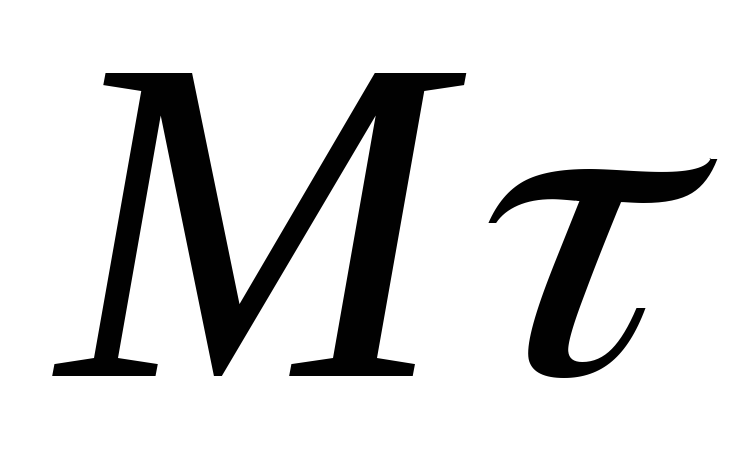
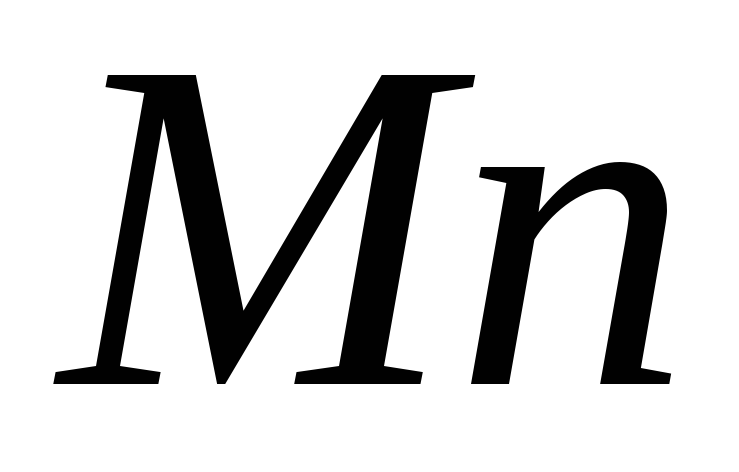
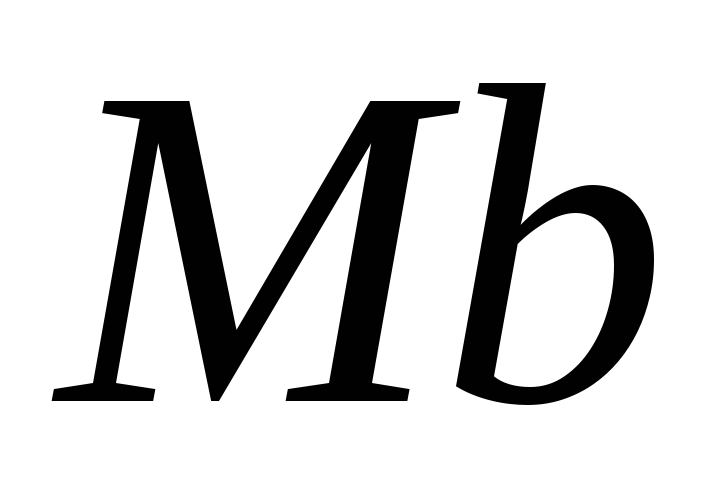
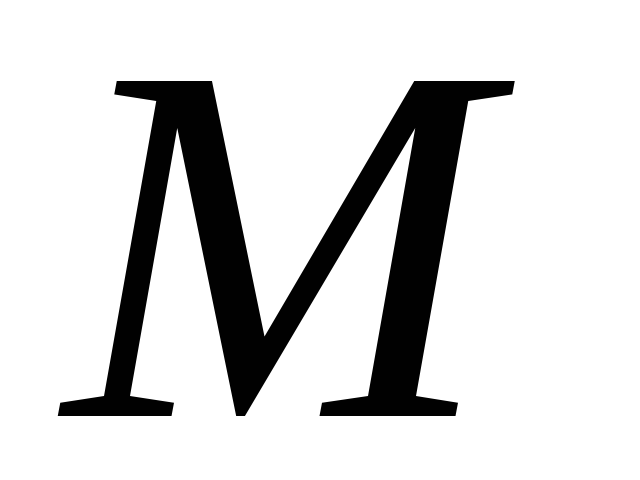
Разложим вектор 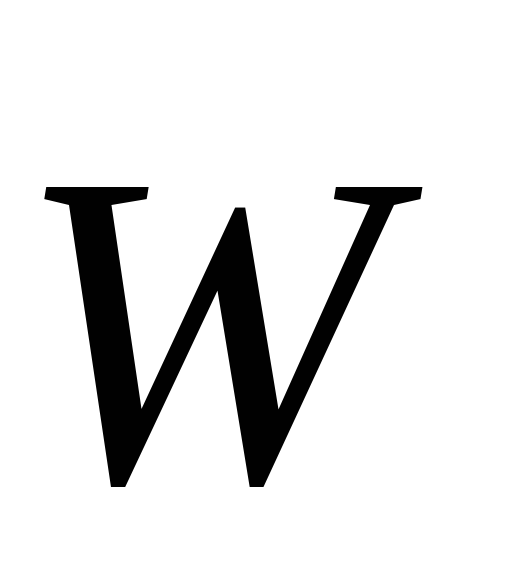
Дифференцируя выражение (1.1.17) скорости точки по времени, получаем
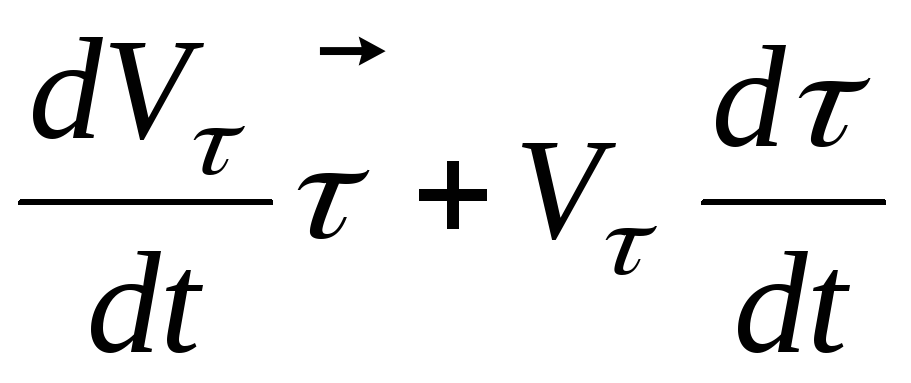
Здесь первое слагаемое – составляющая вектора ускорения по касатель-ной к траектории – 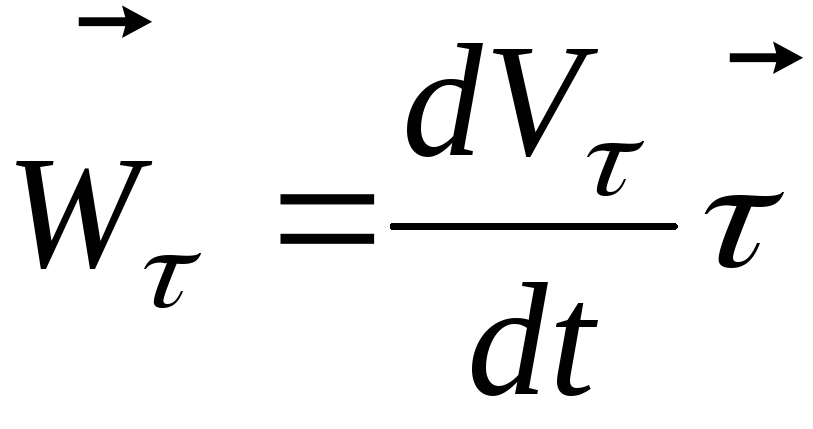
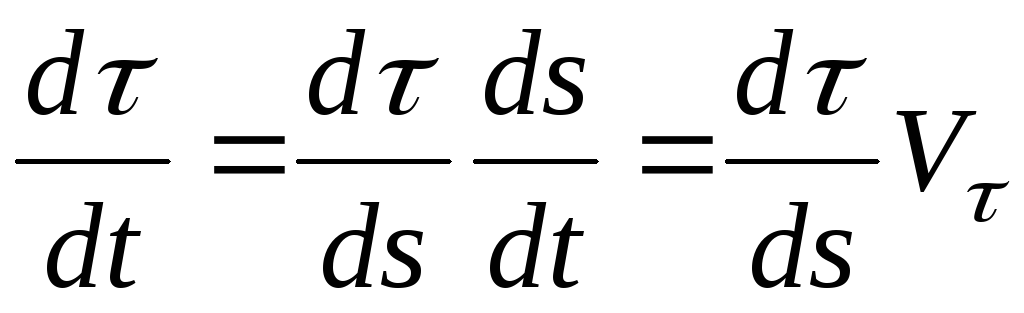
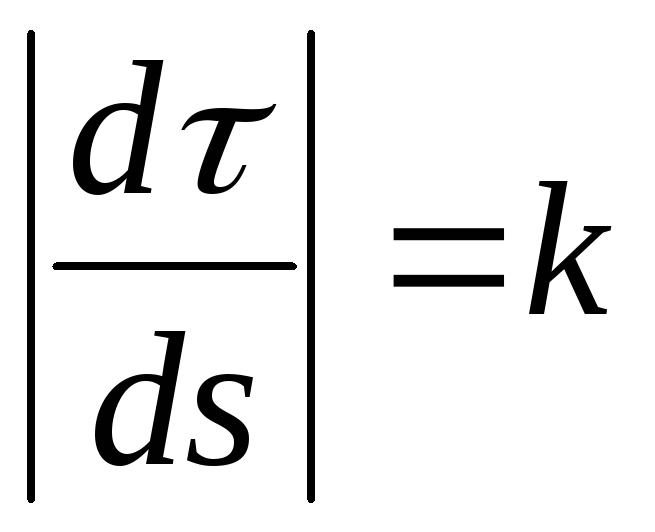
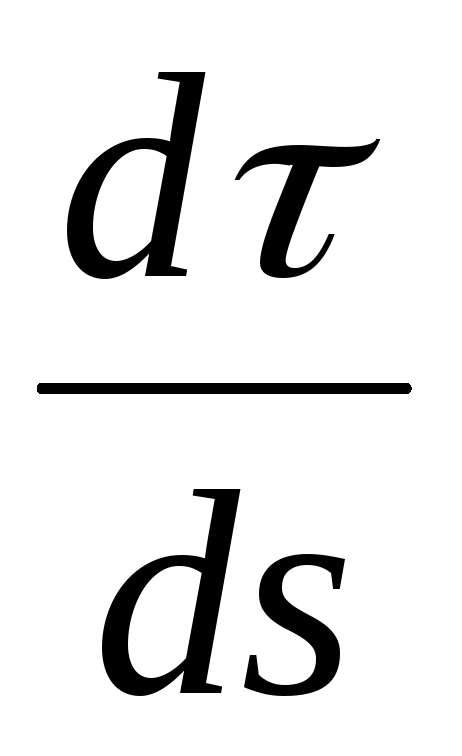

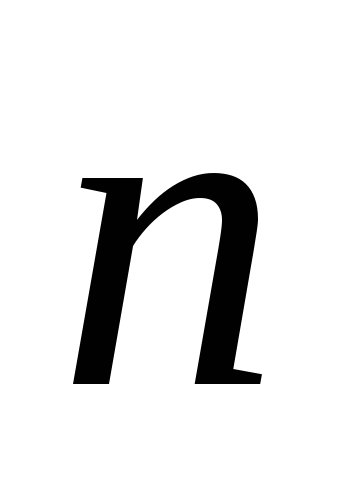
Радиусом кривизны кривой в данной точке 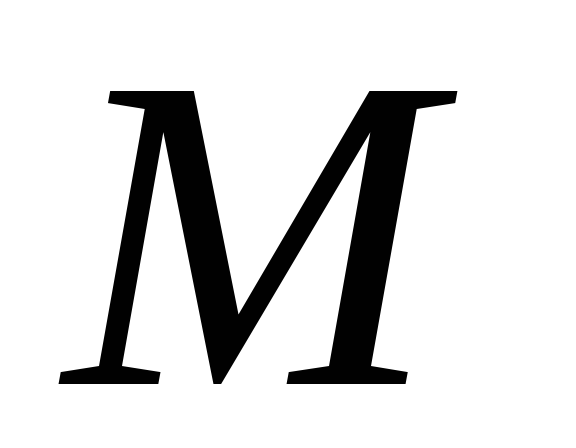
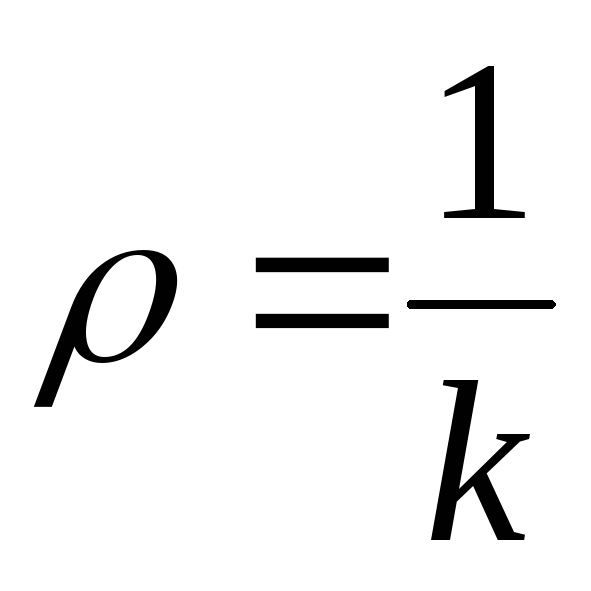
Следовательно, второе слагаемое в формуле (1.1.25) примет вид 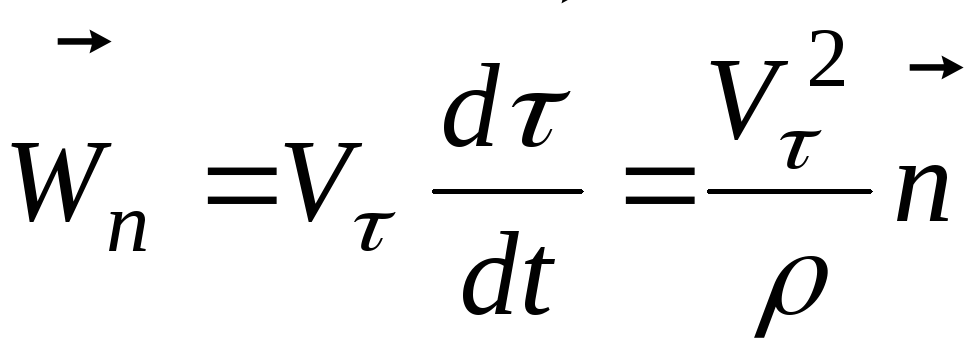
Таким образом, ускорение точки при естественном способе задания её движения раскладывается на две составляющие: — ускорение 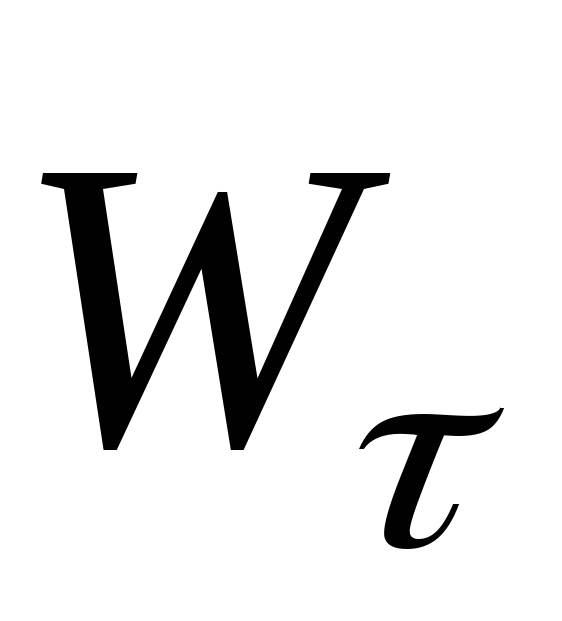
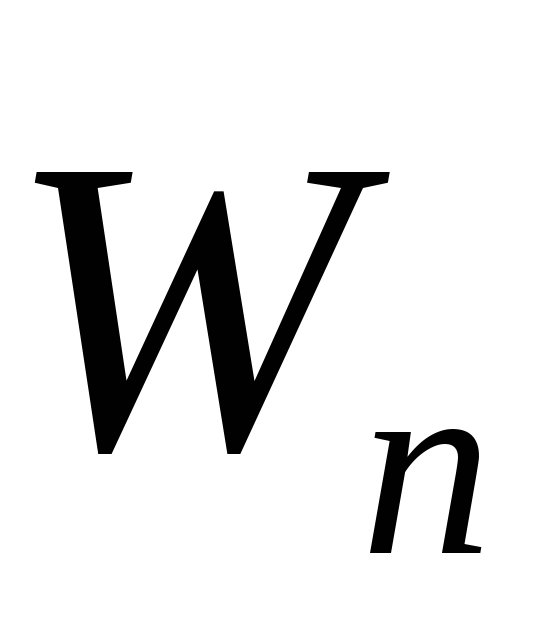
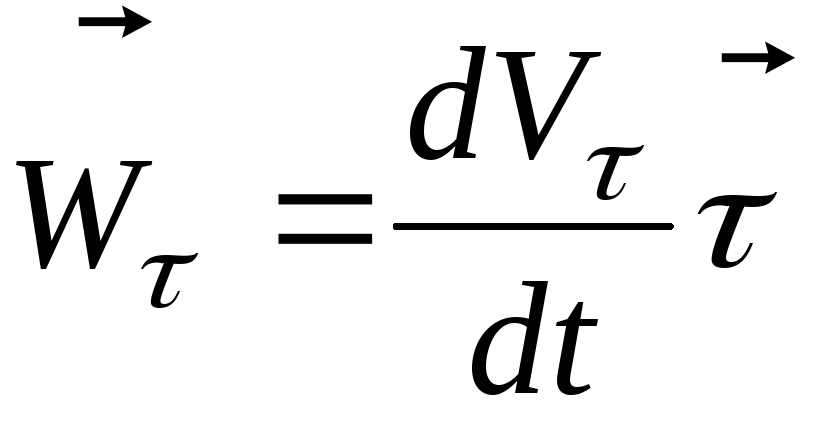

В итоге, формулу (1.1.25) можно представить в виде
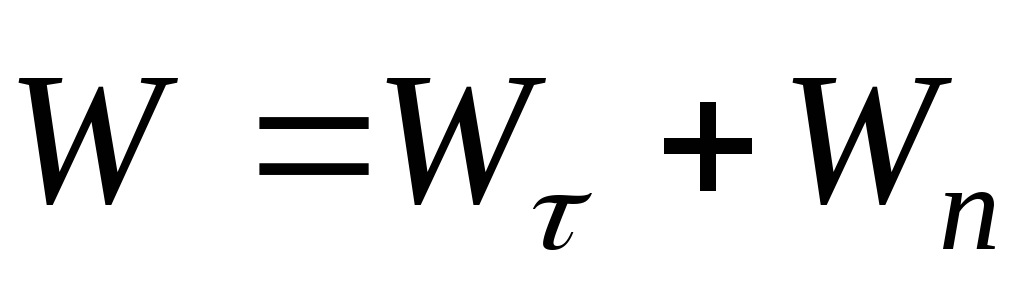
Скалярные множители в (1.1.25) являются проекциями ускорения точки на касательную и главную нормаль:
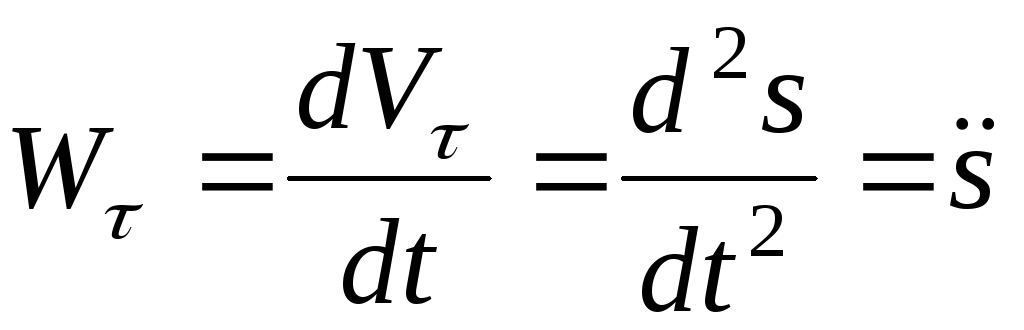
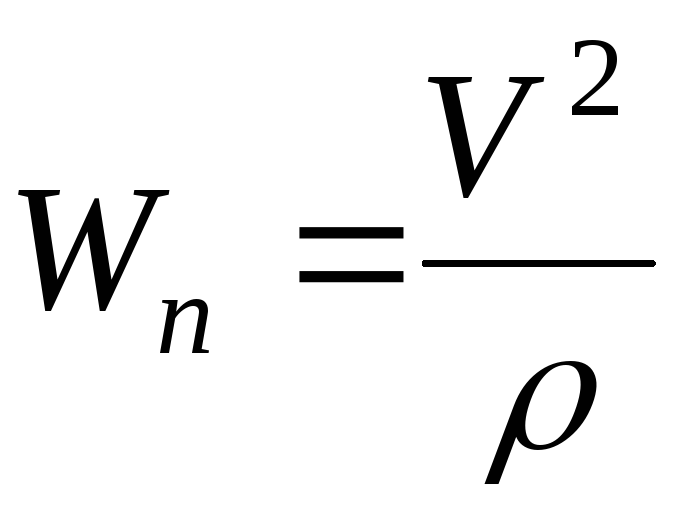
Модуль касательного ускорения равен 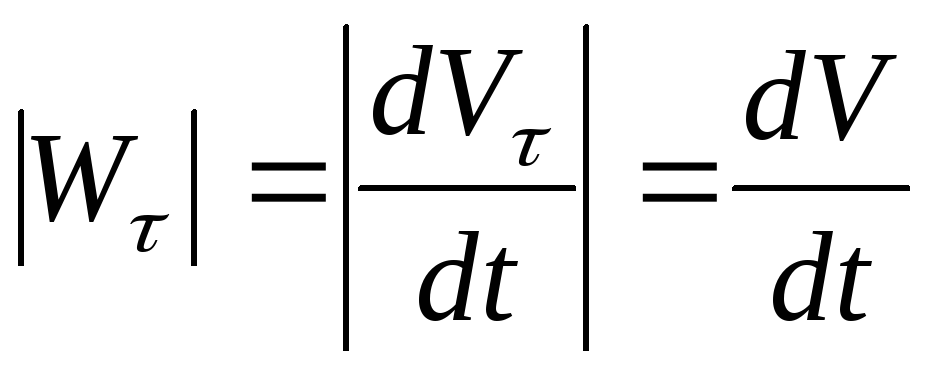
Из зависимости (1.1.25) видно, что вектор ускорения точки 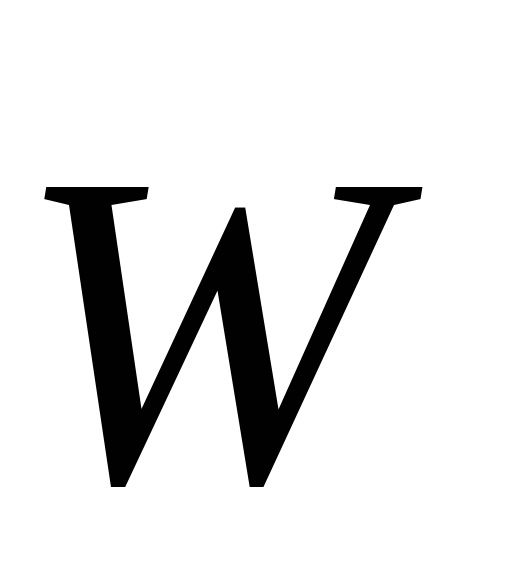
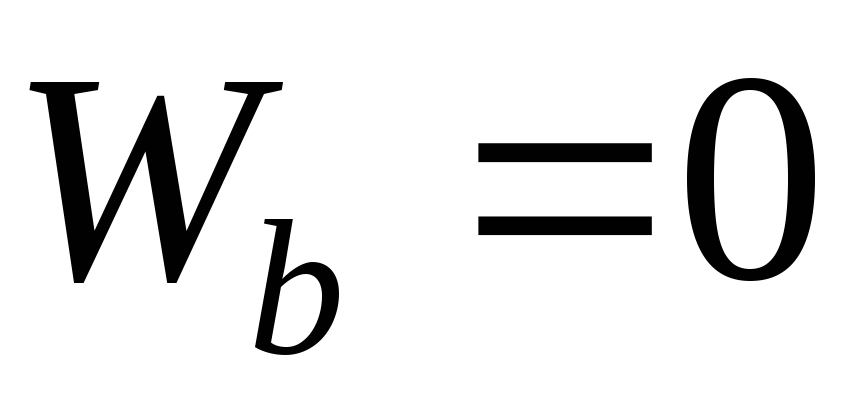
Касательное ускорение 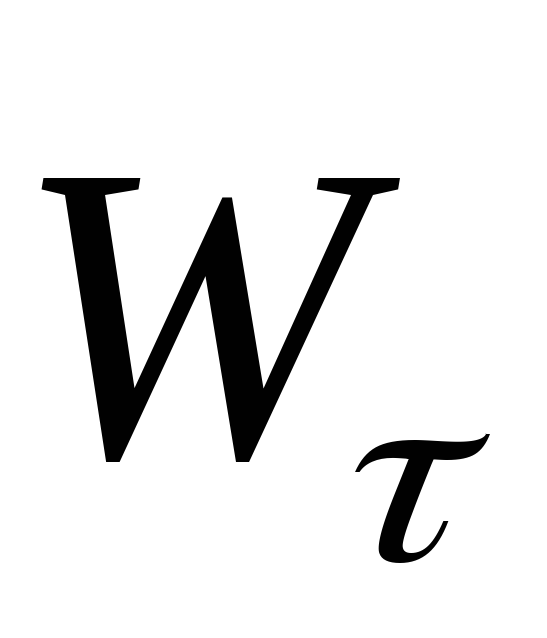

Нормальное ускорение 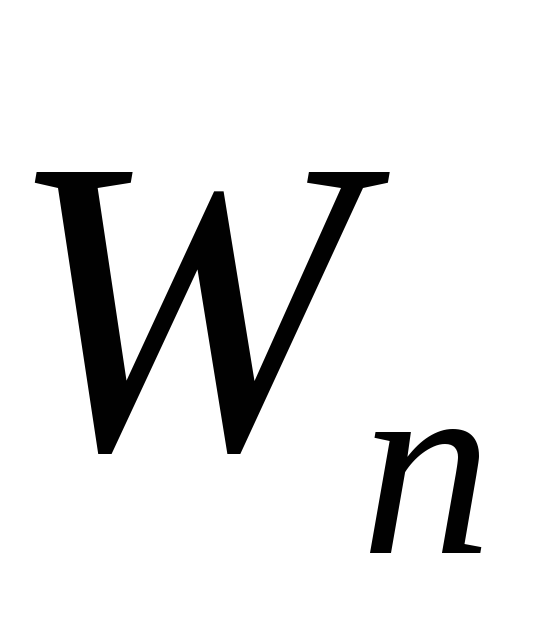

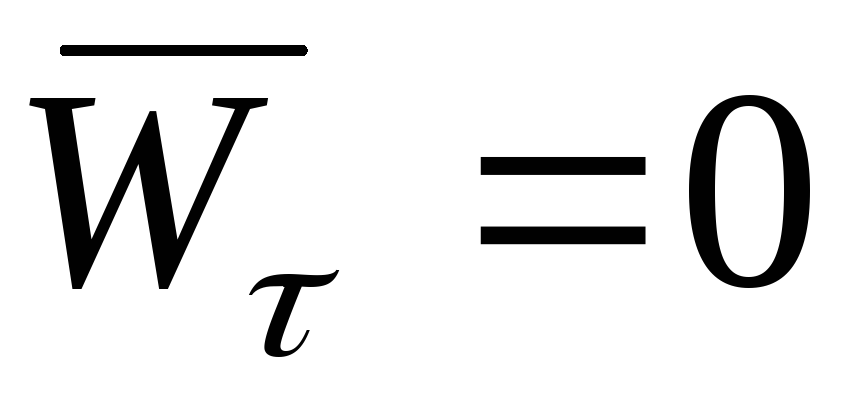
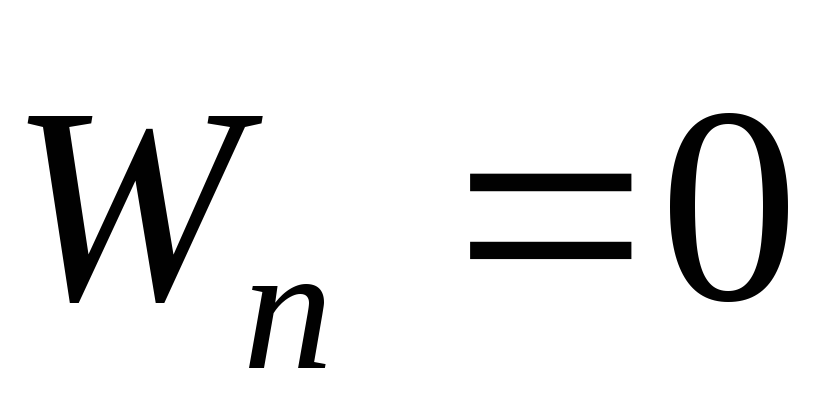
Поскольку векторы 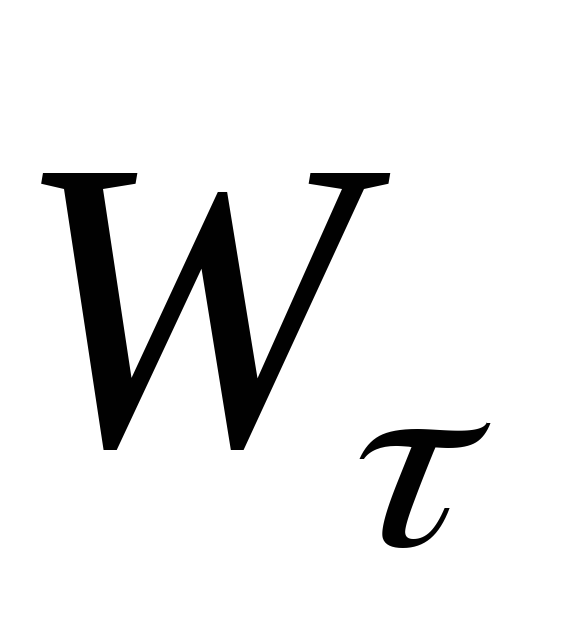
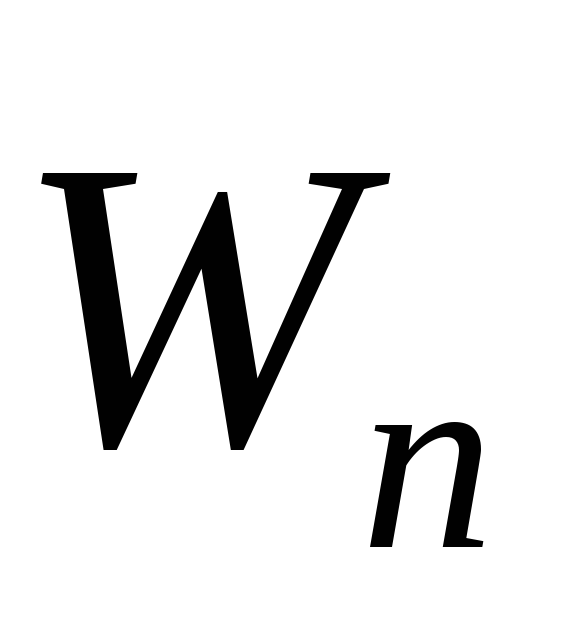
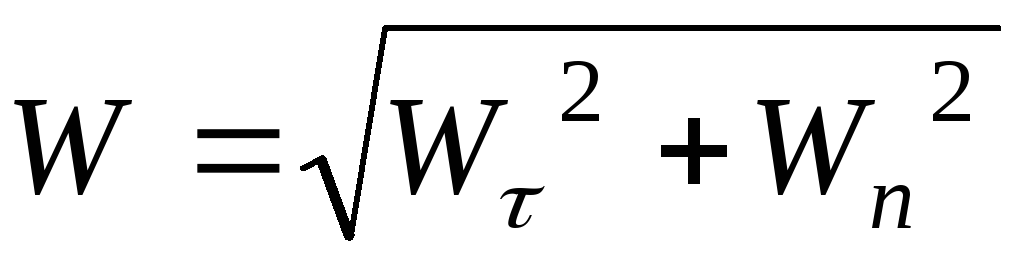
Вопросы для самопроверки по теме 1.1
1. Что является предметом теоретической механики?
2. Что называется механическим движением материальных тел?
3. В чем состоит метод абстракции в механике?
4. Какими способами задается движение точки?
5. Установите связь между векторным и координатным способами задания движения точки.
6. Как определяют траекторию движения точки, если заданы её уравне-ния движения в проекциях на декартовые оси?
7. Дайте определение скорости точки при векторном и координатном способах задания движения.
8. Дайте определение скорости точки при естественном способе задания её движения.
9. Дайте определение ускорения точки при задании её движения векторным и координатным способами.
10. Перечислите естественные оси, их орты и названия координатных плоскостей.
11. Чем орты естественных осей отличаются от ортов осей неподвижной декартовой системы отсчета?
12. Что характеризует касательное ускорение?
13. Что характеризует нормальное ускорение?
14. Как движется точка при 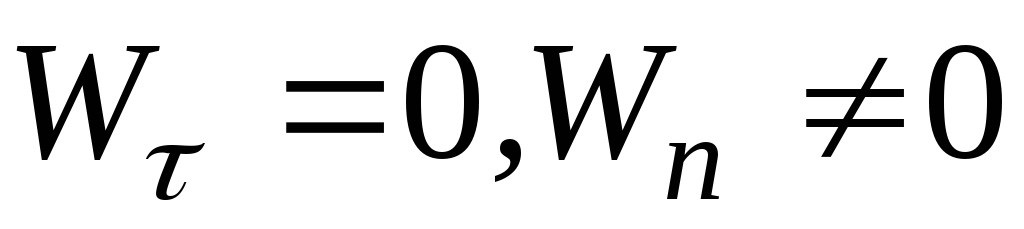
15. Как движется точка при 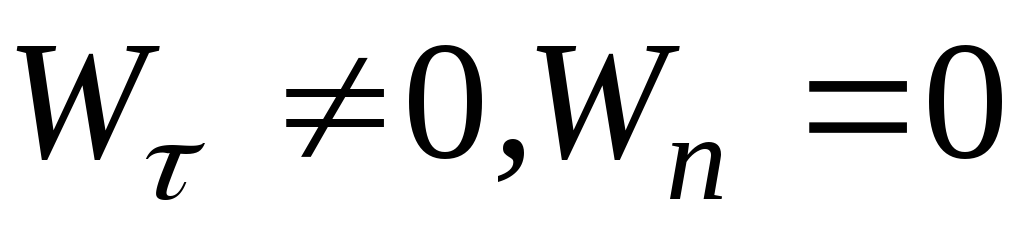
16. Какое движение точки называется равноускоренным, равнозамедлен-ным?
17. Назовите кривые, имеющие постоянный радиус кривизны.
18. Решите самостоятельно задачи 12.4(12.5), 12.9(12.10), 12.14(12.15), 12.22(12.23), 12.25(12.26) из [3].
Источник