Урок способы заданий функции график функции

Конспект урока по теме: «Определение функции. Способы задания функции»

Государственное бюджетное образовательное учреждение лицей № 95

г. Санкт-Петербург

Комягина Наталья Валерьевна, учитель математики

Алгебра 9 класс.

Тема урока «Определение функции. Способы задания функции».

Продолжить знакомство учащихся с понятием «функция»;

Рассмотреть способы задания функции: аналитический, графический, табличный, словесный;

Закрепить эти понятия в ходе выполнения упражнений.

Содействовать развитию познавательного интереса, творческих способностей;

Развитие познавательного интереса,

Развивать память, внимание, логическое мышление, умение анализировать, обобщать, систематизировать и делать выводы,

Формировать умения чётко и ясно излагать свои мысли.

Воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов.

Привитие учащимся навыков самостоятельной работы,

Умение слушать и слышать товарищей.

Воспитывать интерес к предмету и уверенность в том, что при добросовестном отношении, трудолюбии все трудности могут быть преодолены

Тип урока: Урок изучения нового материала.

Оборудование и дополнительные материалы.

Интерактивная презентация PowerPoint , карточки с заданиями

1. Организационный этап.

Здравствуйте, ребята. Я предлагаю вам сегодня поразмышлять о том, что в мире всё зависимо. Наступает весна, длинней становится день.

Придумайте зависимости, которые встречаются в жизни.

Несколько пар приводят свои примеры. Каждая область знаний: физика, химия, биология и другие устанавливает свойства и, что особенно важно, взаимосвязи изучаемых объектов. А математика описывает всё это на своём математическом языке

Изобразить графически зависимость величин из пословицы . ( слайды 1-6)

Разуму свойственно размышлять, то есть связывать причины и следствия, давать ответ на вопрос «почему», выявлять случайное, обнаруживать закономерности, находить в цепи происходящего начала и концы. (Ж.Фабр)

2. Изучение нового материала.

Так как с понятием функция учащиеся уже знакомы с 7-го класса, то должны догадаться о теме урока. Тема нашего урока «Понятие функции. Способы задания функции» (слайд 8)

Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем сильнее натянута тетива лука, тем дальше полетит стрела, чем дольше горит костер, тем теплее будет в пещере.

В те времена редко приходилось сталкиваться с более сложными зависимостями. Но когда возникли первые цивилизации, образовались большие (по тогдашним масштабам) армии, началось строительство гигантских пирамид, то понадобились писцы, которые учитывали поступающие налоги, необходимое для строительства дворцов, подсчитывали, сколько продовольствия надо заготовить для дальних походов. От одного поколения писцов к другому переходили правила решения задач, и чем лучше писец справлялся с ними, тем большим почетом он пользовался.

В ходе изучения истории развития понятия функции был сделан следующий вывод о том, что в древнейшие времена люди видели, что существует какая-то связь между окружающими их явлениями. Они не могли ей дать точное определение и лишь применяли ее на практике. Но после того как было введено понятие переменной величины в науку, расцвела вычислительная математика, была создана буквенная алгебра, и с помощью координат удалось изобразить соответствия между величинами графически. Первым из ученных дал определение функции И. Бернулли в 1817 году: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных» (слайд9)

Но в результате дальнейшего развития понятия функции пришлось отказаться от этого определения, так как оно оказалось неполным и не могло объяснить можно ли одну и ту же функцию задать несколькими аналитическими выражениями. И после длительных споров Лобачевского и Дирихле общепризнанным стало следующие определение: «переменная величина у называется функцией переменной величины х , если каждому значению величины х соответствует единственное, определенное значение величины у » (слайд10)

Это понятие было дано в начале XIX века, и господствует по сей день.

Прочитайте и запишем в тетрадь строгое определение функции. ( слайд 11), подчеркните главные слова в определении.

Согласно определению, рассмотрим примеры и выясним, задана функция или нет?

( слайды 12-15). Повторить определение.

Какие функции вы изучали ранее? (ответы учащихся)

2. 3. Контроль и самоконтроль учащихся.

Проверим свои знания по теме «Квадратичная функция»

Маленький тест (приложение 1) Взаимопроверка (слайд 16)

Источник

Разработка урока по алгебре «Понятие функции. Способы задания функции»(7 класс)

Выбранный для просмотра документ Конспект урока.docx

муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа №45

Разработка урока по теме

«Понятие функции. Способы задания функции»,

алгебра, 7 класс.

Автор учитель математики

МАОУ СОШ №45 г. Калининграда

Гавинская Елена Вячеславовна.

2016 – 2017 учебный год

Автор – Гавинская Елена Вячеславовна

Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45

Предмет – математика (модуль «Алгебра»)

Тема – « Понятие функции. Способы задания функции »

Алгебра. 7 класс: учебник для общеобразовательных учреждений /Ю.М.Колягин и др., — М.: Просвещение, 2012 г.

Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010

ввести понятие функции, зависимой и независимой переменных, рассмотреть способы задания функции.

формирование функциональных представлений на наглядном материале;

формирование способности анализировать, обобщать полученные знания;

развитие навыков применения компьютерных технологий;

формирование логического мышления;

активизировать интерес к получению новых знаний,

воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.

Обоснование выбора методов, средств и форм обучения:

оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.

Оборудование и материалы для урока : проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.

Тип урока : комбинированный.

Целесообразность использования медиа продукта на занятии продиктована следующими факторами:

интенсификацией учебно-воспитательного процесса:

автоматизацией процесса контроля,

улучшением наглядности изучаемого материала,

увеличением количества предлагаемой информации,

уменьшением времени подачи материала;

повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.

Обоснование выбора форм и методов работы на обобщающем уроке по теме «Понятие функции. Способы задания функции» и методические рекомендации по применению презентации на уроке.

Тема « Понятие функции. Способы задания функции» входит в тему «Линейная функция и её график» (первый урок по теме) по авторскому планированию Ш.А.Алимова или Ю.М.Колягина. В заданиях ОГЭ прошлых лет указанная тема встречается как основной компонент при решении заданий. Поэтому предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения понятия функции к решению различных заданий . Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.

И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.

Объявляется цель и план урока.

Записывается домашнее задание: №538, 545, 547.

2.Актуализация опорных знаний.

С комментированием у доски (наиболее подготовленный учащийся) решается №556 .

3.Изложение нового материала.

С помощью презентации и фронтальной беседы вводится понятие функции, независимой и зависимой переменной, рассматриваются способы задания функции. Слайды №3 — №16 .

4. Гимнастика для глаз.

5. Закрепление первичных знаний.

Учащиеся работают в парах, выполняют задания, предложенные на слайдах №23 — №25.

В это время учитель помогает учащимся группы А (которые сидят вместе за одним столом) выполнить те же задания. При необходимости учитель оказывает помощь и остальным ребятам. По окончании работы – фронтальная проверка с обсуждением трудностей, с которыми столкнулись ребята при выполнении указанных заданий.

7.Подведение итогов урока, выставление отметок.

Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?

Анкетирование можно провести с помощью системы Verdict:

Источник

Конспект урока по математике «Функция и способы ее задания»

Описание разработки

Задачи:

Определить виды величин.

Напомнить понятие функции, ее области определения и множества значений.

Рассмотреть способы задания функции.

Закрепить полученные знания при решении задач.

Ход урока

Сообщение темы и цели урока.

Повторение изученного материала.

В математике одним из важных понятий является понятие ФУНКЦИИ. Как вы понимаете это слово? Вспомним пройденное за курс алгебры 7 — 9 класса. (Ответы учеников. )

Функцией у от х называется такое соответствие между переменными х и у, при котором каждому значению х соответствует не более одного значения у.

Функцию можно задать формулой, таблицей, графиком.

Устная работа

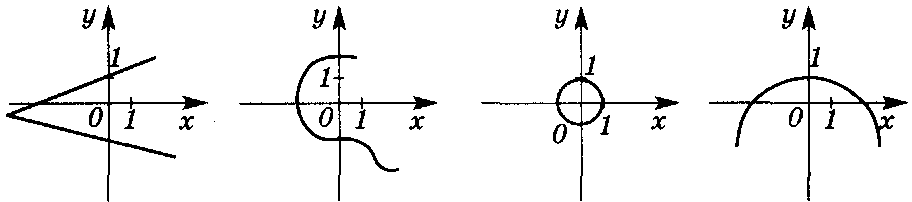
Среди данных линий найти такую, которая является графиком какой — либо функции.

Решение: На первых трех графиках имеются точки с одинаковыми абсциссами и разными ординатами. Это значит, что на этих линиях одному и тому же значению х соответствует более одного значения у, то есть эти линии не являются графиками функций. На четвертом графике каждому значению х соответствует не более одного значения у – это график функции.

Среди данных таблиц найдите такую, которая является таблицей функции.

Решение: В первой и второй таблице имеются значения х, которым соответствуют два разных значения у, то есть эти таблицы не являются таблицами функций. В третьей таблице каждому значению х соответствует не более одного значения у – это таблица функции.

Изучение нового материала

Рассмотрим понятие функции более широко.

В своей практической деятельности человек сталкивается с величинами различной природы: длина, площадь, объем, масса, температура, вес и т. д.

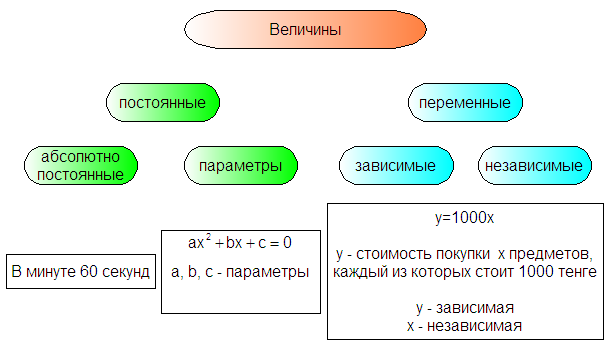
В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т. е. не меняются; другие наоборот, принимают различные значения.

Все величины, изучаемые в математике, делятся на постоянные и переменные. (Формулируются соответствующие определения)

Весь материал – смотрите документ.

Содержимое разработки

Тема: Функция и способы ее задания.

Определить виды величин.

Напомнить понятие функции, ее области определения и множества значений.

Рассмотреть способы задания функции.

Закрепить полученные знания при решении задач.

Сообщение темы и цели урока.

Повторение изученного материала.

В математике одним из важных понятий является понятие ФУНКЦИИ. Как вы понимаете это слово? Вспомним пройденное за курс алгебры 7-9 класса. (Ответы учеников.)

Функцией у от х называется такое соответствие между переменными х и у, при котором каждому значению х соответствует не более одного значения у.

Функцию можно задать формулой, таблицей, графиком.

Среди данных линий найти такую, которая является графиком какой-либо функции.

Решение: На первых трех графиках имеются точки с одинаковыми абсциссами и разными ординатами. Это значит, что на этих линиях одному и тому же значению х соответствует более одного значения у, то есть эти линии не являются графиками функций. На четвертом графике каждому значению х соответствует не более одного значения у – это график функции.

Среди данных таблиц найдите такую, которая является таблицей функции.

Решение: В первой и второй таблице имеются значения х, которым соответствуют два разных значения у, то есть эти таблицы не являются таблицами функций. В третьей таблице каждому значению х соответствует не более одного значения у – это таблица функции.

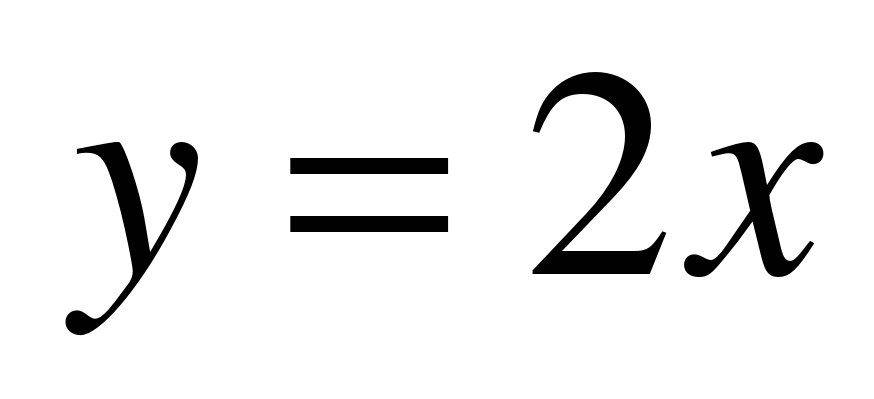
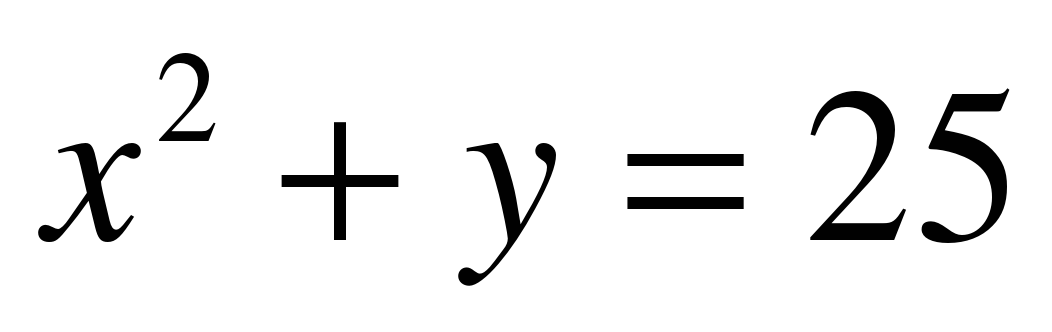
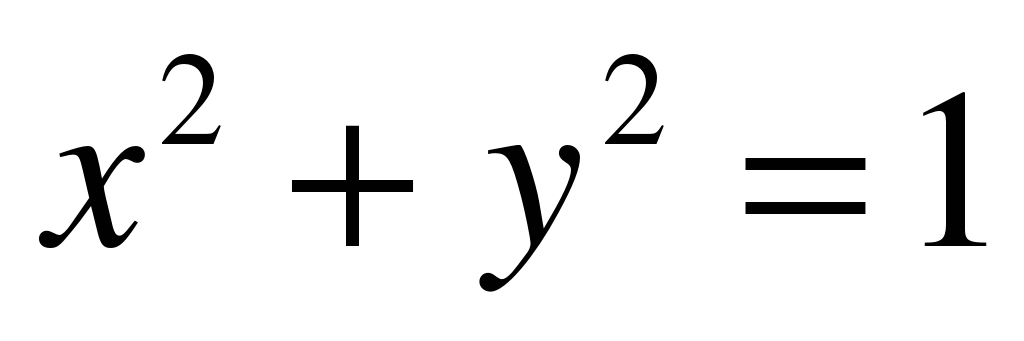
Среди формул а) ; б) ; в) найти такую, которая задает функцию.

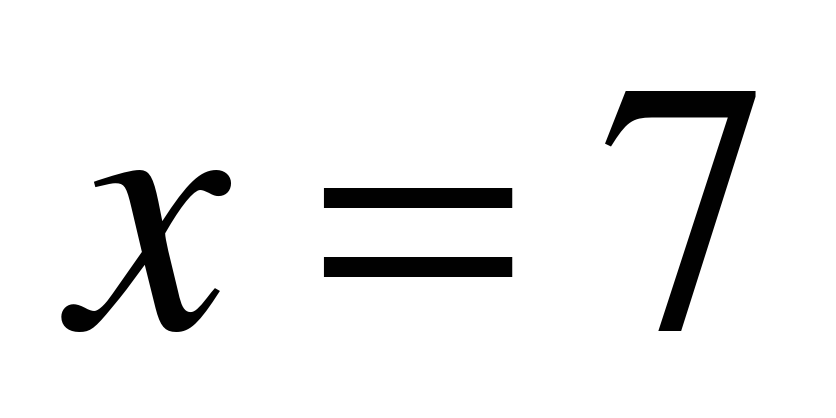
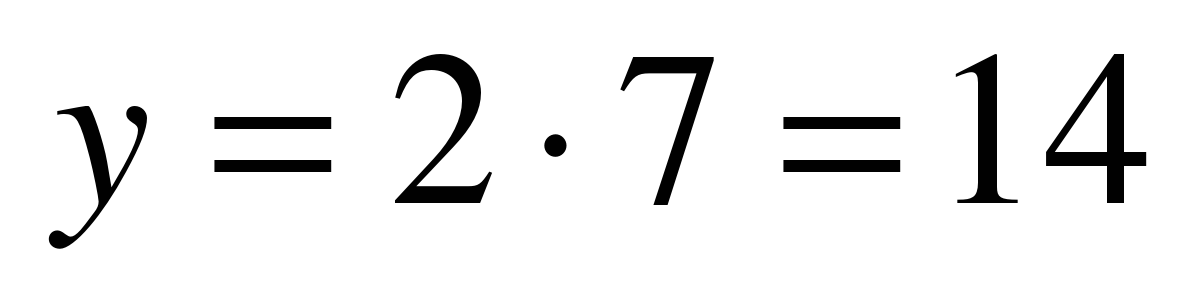
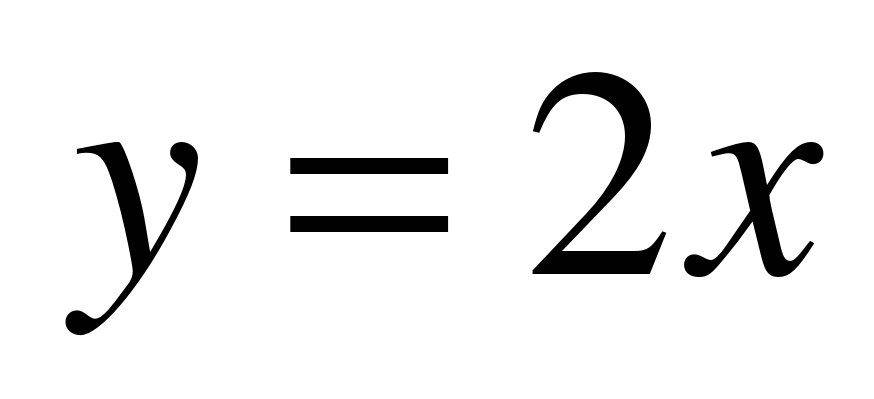
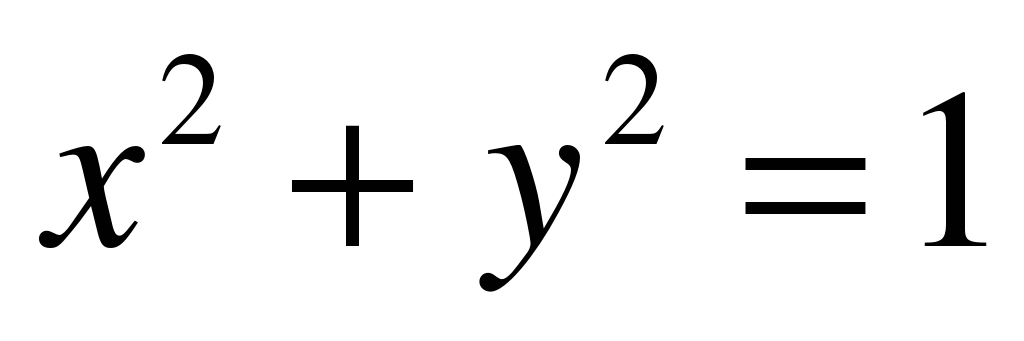
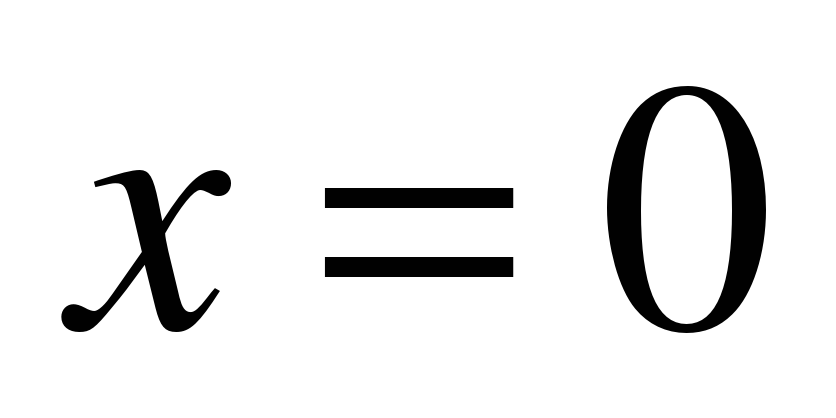
Решение: а, б) Для любого значения х по данной формуле значение у находится единственным образом, например, при получим, что , значит – формула, задающая функцию у от х. в) Формула не задает функцию, так как, например, значению , можно найти два соответствующих значения у: 1 и -1.

Изучение нового материала

Рассмотрим понятие функции более широко.

В своей практической деятельности человек сталкивается с величинами различной природы: длина, площадь, объем, масса, температура, вес и т.д.

В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т.е. не меняются; другие наоборот, принимают различные значения.

Все величины, изучаемые в математике, делятся на постоянные и переменные. (Формулируются соответствующие определения)

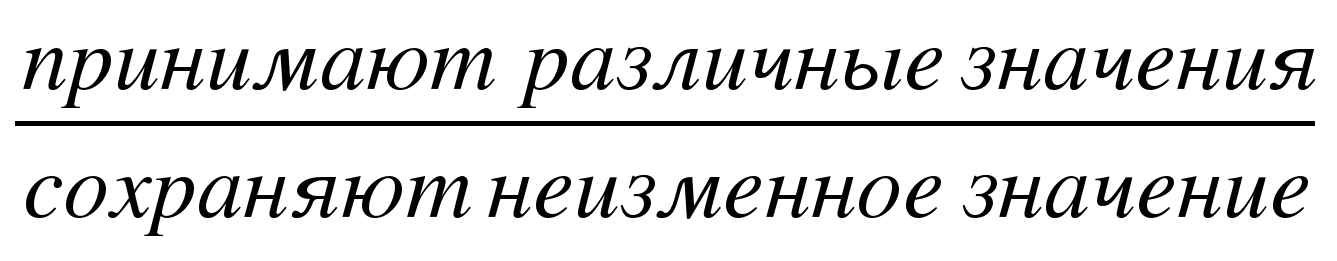
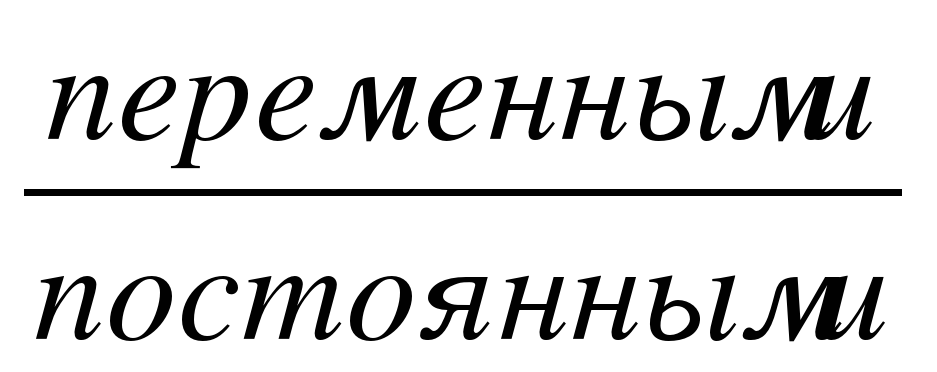
Те из величин, которые в рассматриваемом процессе называются величинами.

Определение. Правило, или закономерность, при котором каждому значению х из множества Х соответствует единственное значение у из множества Y, называется функцией. Обозначение: .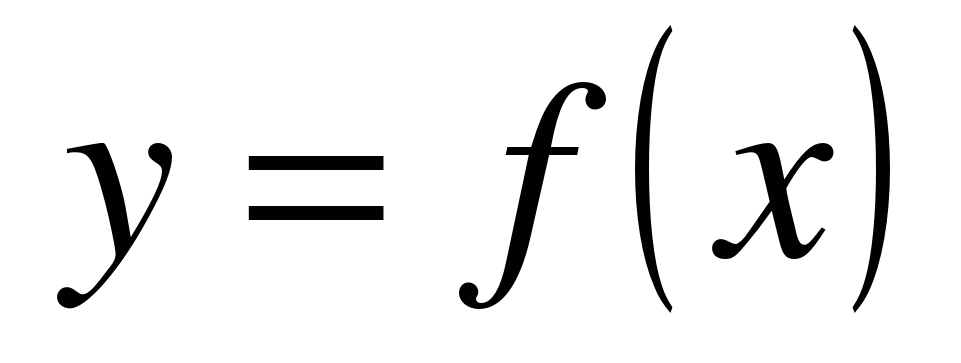

Уточним смысл некоторых понятий, известных вам из курса алгебры 7-9 класса. (Ученики формулируют, учитель при необходимости корректирует. Формулировки выводятся на экран.)

Источник