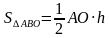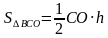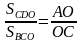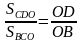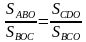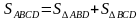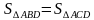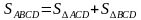Урок решения одной задачи разными способами

Конспект урока математики по теме: «Решение задач разными способами»
план-конспект урока по математике (1 класс) по теме

Конспект урока с использованием деятельностного подхода.

Скачать:

Вложение	Размер
reshenie_zadach_raznymi_sposobami.docx	76.11 КБ

Предварительный просмотр:

Тип урока: открытие новых знаний.

Тема: Решение задач разными способами.

1. предметные: учить решать задачи разными способами; совершенствовать умение составлять модель к задаче;
2. метапредметные : способствовать овладению способностью принимать и сохранять цели и задачи учебной деятельности; формировать умения планировать, контролировать и оценивать учебные действия;
3. личностные: развивать мотивы учебной деятельности; развивать навыки конструктивного сотрудничества со сверстниками и учителем.

Формы организации познавательной деятельности: групповая, индивидуальная, фронтальная.

1. по источнику знаний : словесные, практические;
2. по уровню познавательной активности: частично — поисковый;
3. по принципу расчленения или соединения знаний: аналитический, сравнительный.

Оборудование: карточки со схемами слов, фишки, карточки для парной и групповой работы, презентация на интерактивной доске МIMIO .

Источник

Урок одной задачи

Урок одной задачи – это поиск разных способов решения одной задачи. Ученик имеет возможность найти тот способ решения, который ему понятен. Учет подструктур математического мышления побуждает учащихся к поиску различных приемов решения. Психологи установили, что решение одной задачи разными способами приносит больше пользы, чем решение подряд нескольких однотипных задач.

Просмотр содержимого документа
«Урок одной задачи»

Тема урока: Урок одной задачи

Учитель: Турова Оксана Владимировна

Урок одной задачи – это поиск разных способов решения одной задачи. Ученик имеет возможность найти тот способ решения, который ему понятен. Учет подструктур математического мышления побуждает учащихся к поиску различных приемов решения. Психологи установили, что решение одной задачи разными способами приносит больше пользы, чем решение подряд нескольких однотипных задач.

Решить задачу несколькими способами, учитывая структуры математического мышления. Показать многообразие и красоту математических решений. Создать ситуацию успеха и радости.

Образовательные: обобщить изученный по теме материал, формировать умение применять знания к решению задач;

Развивающие: развивать познавательную активность, творческие способности и интерес к предмету. Индивидуальные способности и критическое мышление;

Воспитательные: учить прислушиваться к мнению товарищей, развивать умение работать в группах, воспитывать у учащихся гибкость мышления.

Организационный момент (2 мин);

Решение задач в группах (15 мин);

Представление решения членами группы (20 мин);

Заключительное слово учителя (5 мин);

Рефлексия, домашнее задание (3 мин).

Учитель объясняет учащимся, что сегодня предстоит необычный урок. Решая задачу по группам и защищая свое решение, они смогут увидеть большие возможности геометрии, когда одну и ту же задачу можно решить разными способами.

Затем учащимся предлагается сесть по группам, выбрать капитана, который будет представлять решение задачи на доске.

Перед уроком класс разбивается на 5 групп (на основе диагностики) по доминантным подструктурам математического мышления: на «топологов», «метристов», «порядковцев» и «алгебраистов».

Решение задач и в группах

Учитель предлагаем приступить к решению задачи.

Задача:

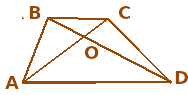
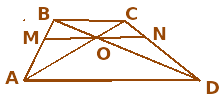
Трапеция разбита диагоналями на четыре треугольника. Докажите, что треугольники, прилежащие к боковым сторонам, равновелики.

В процессе урока учитель подходит к отдельным группам и наблюдает за работой учеников. Роль учителя заключается в том, чтобы в зависимости от доминантного кластера математического мышления детей той или иной группы, найти те подсказки, которые окажут реальную помощь школьникам.

Для группы с доминантной топологической подструктурой естественной подсказкой может быть акцент на использование принадлежности одних треугольников другим, а именно:

— Не видите ли вы треугольник, в который включаются треугольники АОВ и СОD?

-Что является пересечением △АВD и △АСD?

Обычно топологи, опираясь на подсказки, выстраивают следующее доказательство:

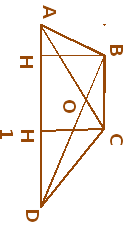
Рассмотрим △АВD и △ACD.

У них общее основание АD и равны высоты ВН=СН₁, тогда

Алгебраическая подструктура позволяет осуществлять не только прямые, но и обратные операции, заменить несколько операций одной, вычислить части и собрать их в единое целое. Для них удобны следующие подсказки:

— Используйте метод от противного;

-Проведите через точку О отрезок MN ││ BC и докажите, что OM=ON

Группой алгебраистов были представлены следующие решения:

Пусть S_△ABO ≠ S_△CDO, тогда S_△ABD ≠ S_△ACD и ВС ││ АD.

Получили противоречие с тем, что АВСД трапеция. Значит, S_△ABO = S_△CDO

Проведем MN ││ BC, О MN, OM=ON

Треугольники АВО и СВО состоят из двух треугольников, площади которых равны.

Метрическая подструктура акцентирует внимание человека на количественных преобразованиях и позволяет пересчитывать, определять конкретные числовые значения.

Хорошей подсказкой является следующая:

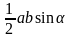
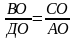
-По формуле S_△ = вычислите S_△ABO и S_△CDO, используя подобие △ВСО и △АДО

,

АО·ВО =СО·ДО │·

АО·ВО = СО·ДО,

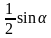
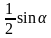
Для проективистов очевидной и полезной будет подсказка:

— заменить («спроецировать») треугольники на одну из сторон каждого из них, то есть на отрезки диагоналей трапеции.

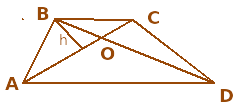
Аналогично,

△ВСО ∽ △АДО, значит ,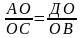

Для порядковцев важны такие отношения, как «больше-меньше», «равно». Они любят действовать последовательно, поэтому для них предлагаются подсказки:

— Установите последовательность величин площадей треугольников от большего к меньшему;

— Есть ли среди них треугольники с равными площадями?

— На каком основании вы можете заключить, что площадь каждого последующего треугольника меньше площади предыдущего?

— Попробуйте последовательно заменять площадь трапеции суммой площадей больших треугольников, а сумму последних – суммой площадей меньших треугольников;

Разные дети, после разного количества подсказок приходят к следующим решениям:

Тогда,

Заменяя площади больших треугольников площадями меньшими, получаем:

(1)

) (2)

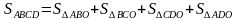
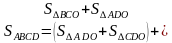
Приравниваем правые части (1) и (2), приводим подобные слагаемые:

)

=

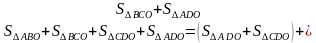
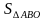
Используя формулу , замечаем =

=

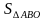
Представление решения членами группы

Каждая группа выступает со своим доказательством.

Это очень важный этап урока, так как только после того как школьник усвоил решение адекватное своему кластеру, он способен осознанно и неформально овладеть другими способами решения.

Рефлексия. Домашнее задание.

Задача 2: Докажите, что медиана разбивает треугольник на шесть равновеликих треугольников.

Источник

Конспект урока математики « Решение задач… (разными способами).»

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ, СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 43 Г. ТОМСКА

Кулеш Валентина Васильевна

учитель начальных классов

высшая квалификационная категория

в 4 классе V вида для детей с ТНР

Тема: « Решение задач… (разными способами).»

Цели: 1. Формировать умения решать текстовые задачи и видеть

различные способы их решения.

2. Закрепить алгоритм умножения и деления на однозначное

3. Способствовать развитию учебной и познавательной

У- Заливистый школьный звонок

Позвал нас опять на урок.

Будьте все внимательны,

А ещё — старательны.

У- Урок математики.

Тема урока записана на доске. Но она записана не полностью. Предложение не закончено!

А неизвестность — одних — пугает,

Но и тем и другим хочется раскрыть тайну. Не так ли?

Интересно, у вас с какими существительными ассоциируются прилагательные: тайное,

Д — ( М.б. – клад, сокровище … .)

У — Я приглашаю вас на поиски сокровищ.

— А какими д. б. кладоискатели и почему?

Д — ( м.б. — настойчивыми, терпеливыми, дружными…)

У — Нам сегодня пригодятся эти качества.

У — К любому путешествию нужна подготовка.

Нам надо потренироваться в счёте.

( На доске — плакат.)

У — * Найдите число, в котором 26 сотен. Уменьшите его

* Найдите число, выражающее единицы массы.

Разделите на 60 кг.

* Найдите число, которым может быть выражена

цена товара. Увеличьте в 15 раз.

* Найдите двузначное чётное число. Умножьте на 30.

* Найдите восьмую часть от числа, обозначающего

У — А сейчас — проверим.

Встаньте те ребята, у которых такие ответы.

(Ключ: 200, 9кг, 75руб, 360, 11м.)

У — В Средние века алхимики были одержимы идеей

создания философского камня, который должен был

превращать все металлы в золото.

— Так, в 1669 году ( а какой это век?) солдат- алхимик

Хенни Бранд смешал 6 мешков твёрдой соли и 3

таких же мешка угля. Получившуюся смесь массой

522 кг он долго прокаливал ( т.е. обжигал на огне.)

— Сколько килограммов каждого вещества он взял

— И получил он… а что — вы узнаете, если задачу

( На доске прикреплены рисунки трёх колб с варианта-

ми ответов. На правильном варианте на обратной

стороне написано « фосфор.»)

У — Как и в тестовых заданиях, я даже предлагаю

Но чтобы получить любой из них — задачу надо

решить, т.е. провести по ней рассуждения.

( Дети решают самостоятельно, устно комментируют.)

Итог: У каждой группы на отдельных листах — краткая

На доску: из одной группы — краткая запись,

из другой группы — решение.

С

2. 522:9=58 (кг) – в 1 мешке

3. 58*6=348 (кг) – соль

4. 58*3=174 (кг) – уголь

или 4. 522-348=174 (кг) – 2 способ.

У – Прочитайте на колбе ответ.

У – Так был открыт фосфор – белый, ядовитый, светящийся ночью порошок.

У – Алхимикам принадлежит еще много открытий и изобретений. Они изобрели химические приборы, массу лекарств, открыли мышьяк, никель.

— Можно ли это считать сокровищами?

Д – Да. Для науки.

У – А мы что с вами открыли для себя?

Д – Два варианта последнего действия.

— Вот так! (С настроением показать большой палец)

— Вот так! (Любым стилем)

— Вот так! (Руки «козырьком»)

— Вот так! (Подпереть щеку рукой)

— Вот так! (надуть щеки и хлопнуть по ним).

VI . Продолжение работы по теме урока. Работа в группах. Межпредметные связи: География.

У – Вам знакомо имя Христофор Колумб?

У – А в 1492 г. (какой это век?) Христофор Колумб по велению испанского короля поплыл на трех кораблях за золотом и специями (а специи тогда ценились на вес золота) в Индию. Но он решил попасть к берегам Индии, не огибая Африку, а плывя на Запад. Привез ли он сокровища, вы узнаете, если решите следующую задачу:

Из 4 метров ткани можно сшить 20 лент на паруса.

Сколько лент получится из 12 метров ткани?

1. 20 : 4 = 5 (л.) из 1 метра

1. 12 : 4 = 3 (р) – в разы больше.

1. 400 : 20 = 20 (см) – 1 лента

2. 1200 : 20 = 60 (л) – будет.

У – Раскрылись все 3 способа. Все 3 корабля повернули домой (обр. сторона).

У – Но Колумб вернулся без золота и пряностей. Он даже не доплыл до Индии. Но он привез великое открытие – Новый Свет – Америку.

У – Можно ли открытие Америки назвать сокровищем?

У – Можно ли сказать, что вы совершили маленькое открытие?

VII . Физминутка для глаз.

Глазки видят всё вокруг –

Обведу я ими круг.

Глазкам видеть всё дано –

Где стена, а где окно.

VIII . Продолжение работы по теме урока.

У – А давайте придумаем аналогичную задачу. А дома вы ее решите несколькими способами.

У – За основу сюжета возьмем желание короля продать за золото те пряности, которые должен был привезти Колумб.

И следующие числа:

6 кг; 48 кг; 24 слитка золота

(Дети работают в группах).

Устно формулируется задача:

Д – 1. 6 кг пряностей можно продать за 24 слитка золота. Сколько стоят 48 кг этих пряностей?

У – И Бранд, и Колумб сделали свои открытия случайно. Мы с вами случайно решили задачи?

Д – Нет. Мы рассуждали….

У – Какие сокровища нашли герои?

У – Какие сокровища нашли мы с вами?

Д – Варианты, разные способы решения.

У – Какая «тайна» скрывалась в теме нашего урока? Допишем ее.

Д – «разными способами».

У – Какое значение слова «сокровище» мы раскрыли?

Д – Новые знания, сбывшаяся мечта,……

У – Да, на любом уроке можно сделать открытие, равноценное кладу.

У – Для того, чтобы вы не забыли исходные данные домашней задачи, я записала их на символах. Возьмите. Прочитайте.

У – Переверните эти символы на другую строну. Обозначьте свое настроение в конце урока после поиска сокровищ.

У – Я благодарю вас за дружную и интересную работу и желаю вам каждому в жизни найти свое сокровище.

XI . Домашнее задание

У –Дома постарайтесь решить задачу разными способами.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 801 человек из 76 регионов

Курс повышения квалификации

Специфика преподавания предмета «Родной (русский) язык» с учетом реализации ФГОС НОО

• Сейчас обучается 313 человек из 58 регионов

Курс повышения квалификации

Скоростное чтение

• Сейчас обучается 619 человек из 79 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-551184

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Правительство предложило потратить до 1 млрд рублей на установку флагов РФ у школ

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российские адвокаты бесплатно проконсультируют детей 19 ноября

Время чтения: 2 минуты

В проекте КоАП отказались от штрафов для школ

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник