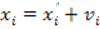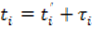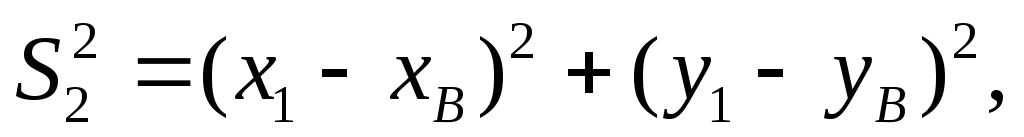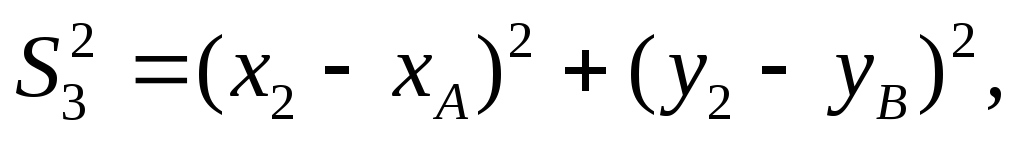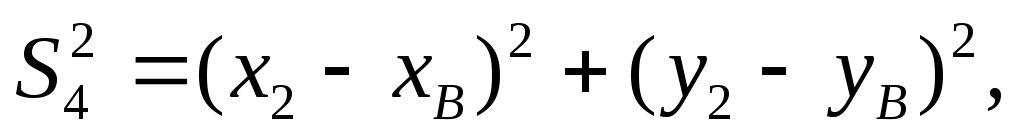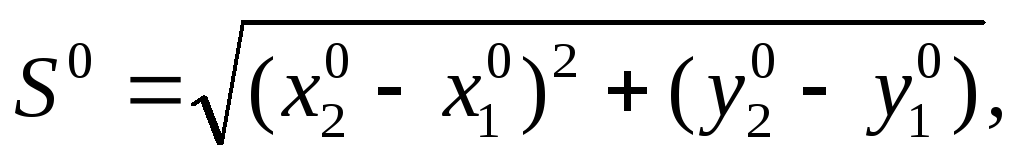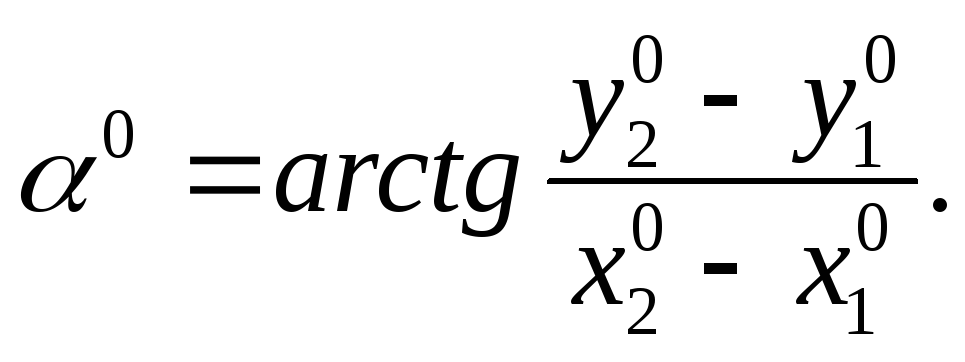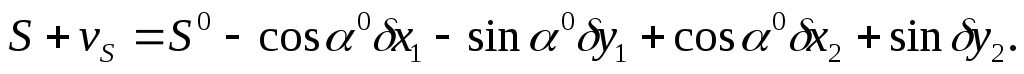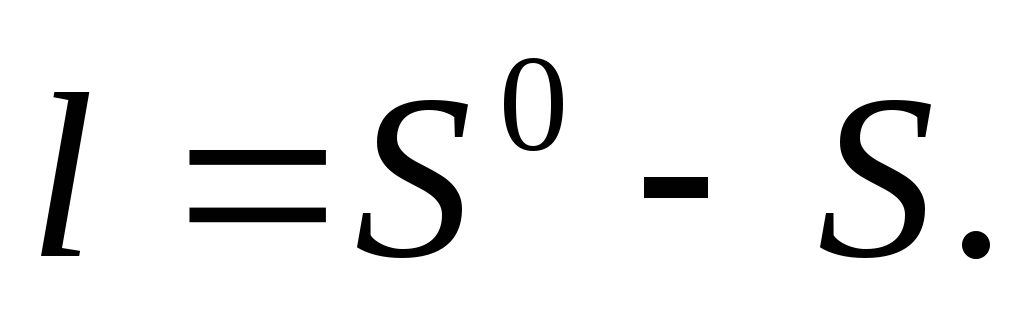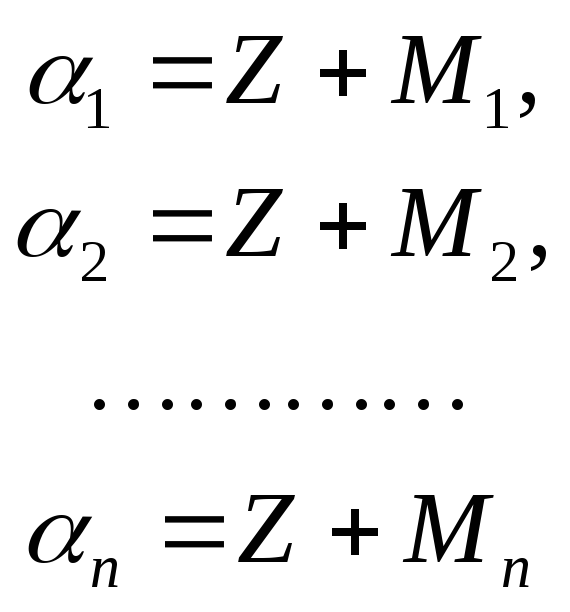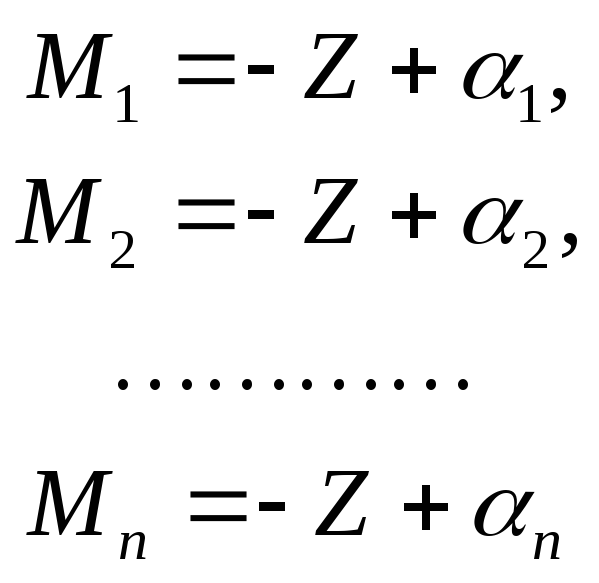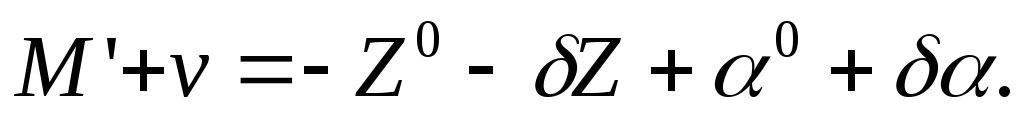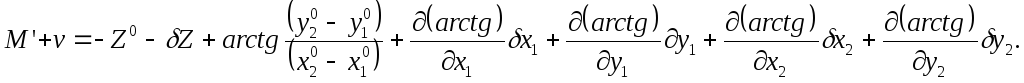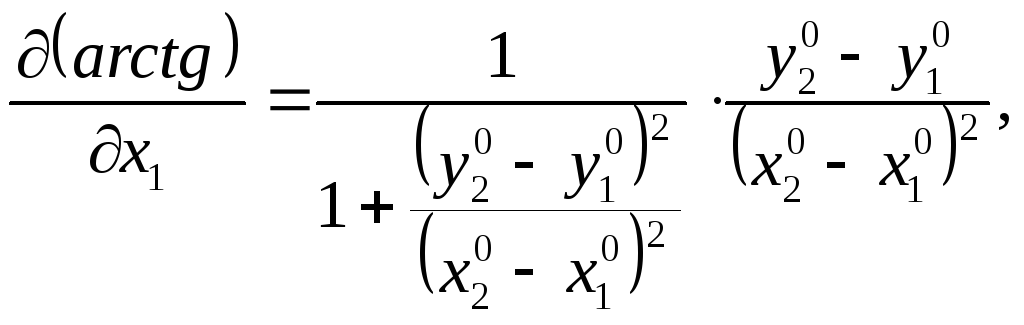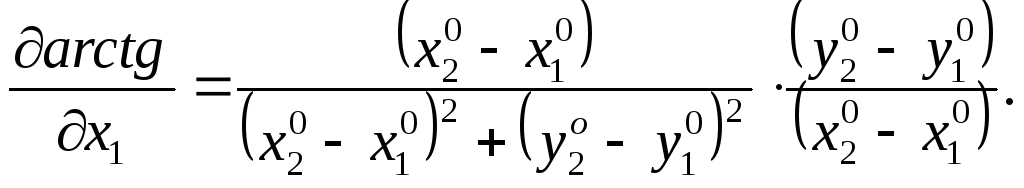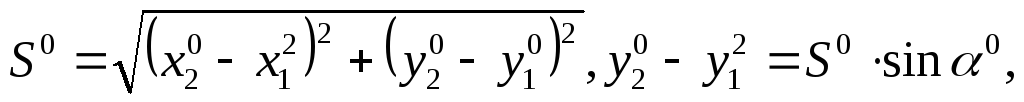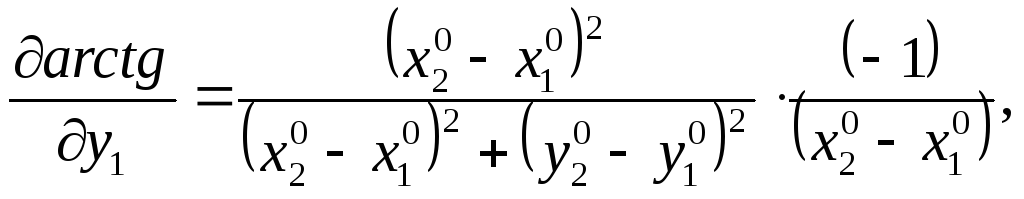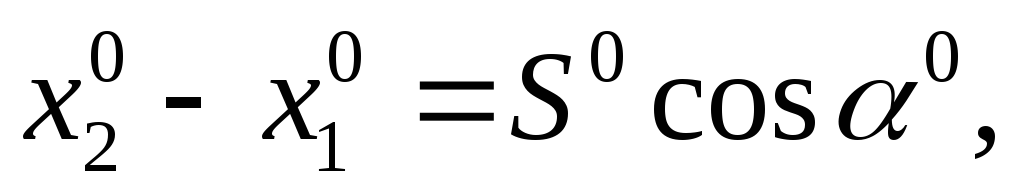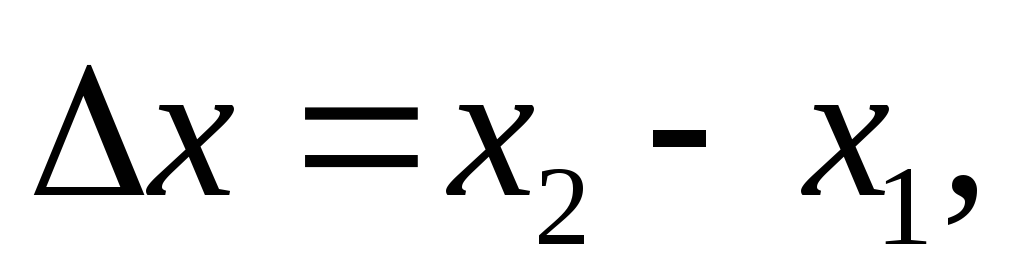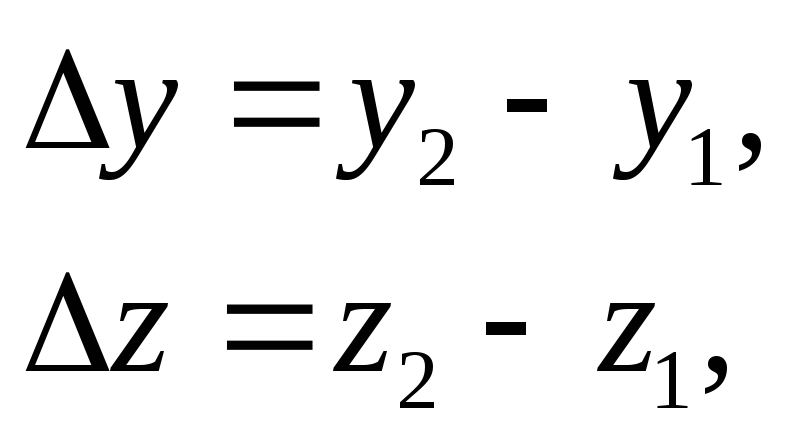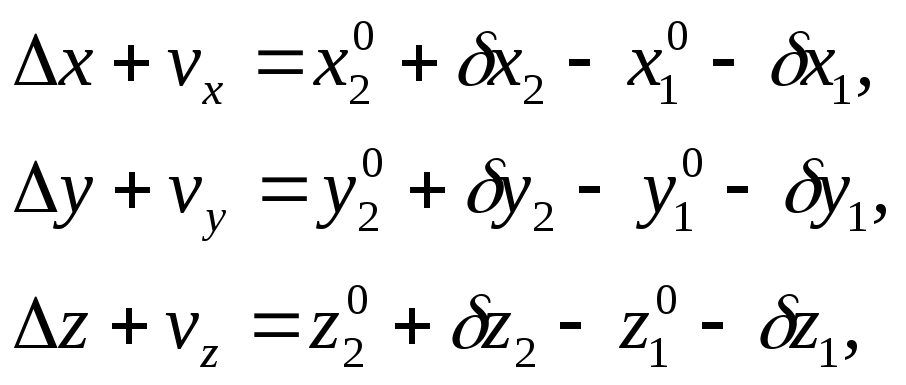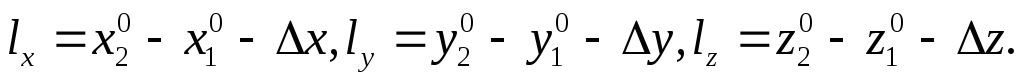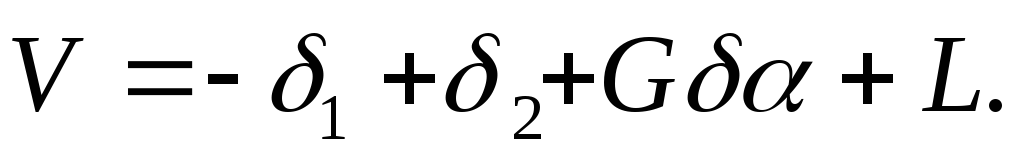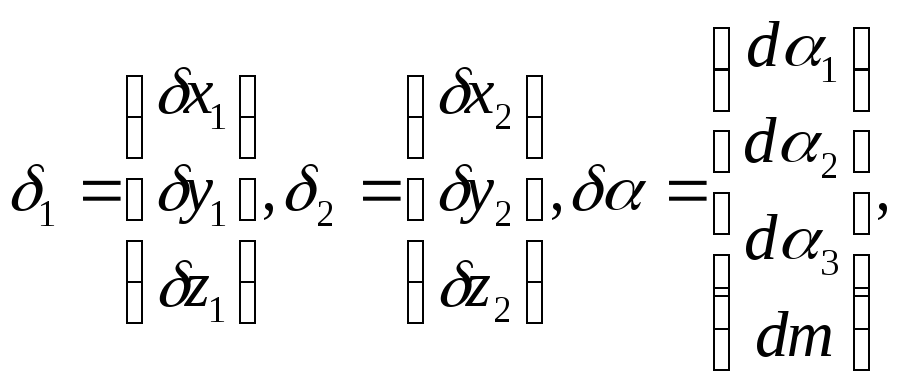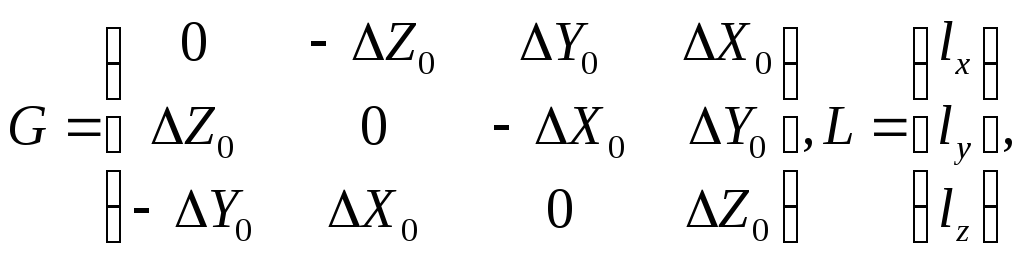Уравнивание триангуляции параметрическим способом

Сущность параметрического способа уравнивания

При уравнивании геодезических сетей параметрическим способом первоначально выбираются так называемые параметры, через которые посредством уравнений связи выражается каждая измеренная величина. Поэтому непосредственно уравниваемыми величинами являются параметры, а затем уже по уравненным значениям параметров вычисляются уравненные значения непосредственно измеренных величин..

Пусть в геодезической сети измерено величин , , …, , из которых величин являются избыточно измеренными. Далее выбирается ряд независимых неизвестных параметров , , …, , через которые могут быть выражены значения измеренных величин , ( ). Число таких параметров должно быть равно числу избыточно измеренных величин. Каждая избыточно измеренная величина в геодезической сети приводит к возникновению одного уравнения связи вида

, ( ) , (7.43)

где , ( ) – истинные значения измеренных величин;

, ( ) – истинные значения параметров.

Уравнения (7.43) называются параметрическими уравнениями связи в общем виде .

Как уже ранее отмечалось, целью уравнительных вычислений является вычисление таких поправок в измеренные величины , при которых удовлетворялись бы все существующие зависимости между элементами сети, причем не только измеренными, но и вычисляемыми. Это означает, что если в левой части выражений (7.43) поставить уравненные значения измеренных величин, то должны измениться и правые части, а именно, должны измениться значения параметров , т.е. в правой части должны стоять соответствующие уравненные значения параметров.

(7.44)

уравненные значения измеренных величин, а через

(7.45)

уравненные значения параметров, где – приближенные значения неизвестных параметров , а – поправки к приближенным значениям параметров. Тогда система уравнений (7.43) может быть переписана в виде

, ( ) , (7.46)

, (7.44)

1. Гудков В.М., Хлебников А.В. Математическая обработка маркшейдерско-геодезических измерений. Учеб. для вузов. – М.: Недра, 1990.– 335 с.

2. Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений. – М.: Недра, 1977. 387 с.

3. Смолич Б.А. Уравнительные вычисления. Учеб. для техникумов – М.: Недра, 1989. – 245 с.

4. Мазмишвили А.И. Теория ошибок и метод наименьших квадратов. – М.: Недра, 1978. 311 с.

5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.1 – М.: Недра, 1970. 456с.

6. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.2 – М.: Недра, 1970. 576с.

7. Бермант А.Ф. Курс математического анализа. Часть 1. – М.: Госуд. изд-во физ-мат. литературы. 1959, 466 с.

8. Селиханович В.Г. Геодезия. Учеб. для вузов.Ч. II – М.: Недра, 1981. 544 с.

Источник

Проекция Гаусса-Крюгера. Элементы геометрии земного эллипсоида. Радиусы кривизны главных нормальных сечений и параллели, средний радиус кривизны , страница 14

§3. Уравнивание сети триангуляции параметрическим способом.

В параметрическом способе уравнивания на основании функциональных зависимостей между определенными неизвестными и измеренными величинами составляют уравнения поправок.

Сущность способа уравнивания заключается в следующем: сначала вычисляем приближенные значения координат определяемых пунктов, а затем составляют уравнения поправок для всех измеренных углов и линий.

Поправки в измеренные углы получаем через поправки координат.

Последовательность уравнивания параметрическим способом:

1. Определяем число избыточных измерений.

2. Выбираем параметры, чтобы они не имели математических связей между собой. Параметрами могут являться непосредственно измеренные углы треугольника и стороны, а также координаты пунктов. Число таких параметров должно равняться числу необходимых измерений. Важно, чтобы параметрические уравнения поправок, составленные с помощью этих параметров, были простые.

3. Все измеренные величины выражают в виде функций выбранных параметров

, где

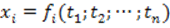
4. Находим приближенные значения параметров .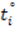

5. Приводим функции к линейному виду, а для этого, вычисляем коэффициенты и свободные члены параметрических уравнений поправок.

6. Составляем и решаем систему нормальных уравнений, в результате чего получаем поправки .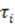

7. Вычисляем значение поправок 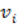в результаты измерений.

8. Находим уравненные значения измеренных величин и параметров

9. Осуществляем контроль выполненного уравнивания.

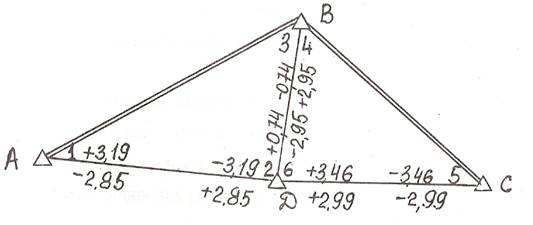
А теперь рассмотрим уравнивание на конкретном примере:

Примечание: по каждому нетвердому направлению выписаны коэффициенты a и b направлений (см. таблицу №4)

Источник

§ 154. Параметрический способ уравнивания

При уравнивании сложных по построению геодезических сетей, в которых имеется обычно большое число избыточных измерений, применение коррелатного способа является практически менее выгодным. Это связано с тем, что в сложных сетях образуется сравнительно большое число геометрических условий (см. § 151), т.е. возникает необходимость решения значительного числа нормальных уравнений. При уравнивании сложных геодезических сетей предпочтение отдают параметрическому способу. В данном случае его рекомендуется применять практически для любых построений: обширных геодезических сетей триангуляции и трилатерации, для весьма сложных фигур триангуляции 3 и 4 классов, в схемах различных линейноугловых построений и др.

Чаще всего при уравнивании плановых геодезических построений параметрическим способом в качестве неизвестных величин (или необходимых параметров t j ) выбирают координаты определяемых пунктов, для которых из предварительных вычислений находят приближенные значения t j o , а затем

определяют поправки τ j к этим приближенным значениям. В качестве уравниваемых величин в плановых построениях принимают измеренные направления, углы, дирекционные углы (азимуты), длины сторон сетей. Промежуточными уравниваемыми величинами (как косвенными величинами) могут явиться и приращения координат точек планового построения.

Для нахождения поправок при уравнивании параметрическим способом необходимо составить параметрические уравнения связи, которые в полной мере обеспечат решение поставленной задачи. Все измеренные величины практически можно выразить через координаты точек сети, т.е. через выбранные параметры t j , что и требуется при уравнивании параметрическим способом. Так, дирекционные углы α и длины s сторон можно найти по разностям координат, горизонтальные углы, в свою очередь, выразить через разность дирекционных углов и т.п.

Рассмотрим различные виды уравнений поправок, применяемых при уравнивании параметрическим способом.

Уравнение поправок для измеренного дирекционного угла находится из параметрического уравнения связи между дирекционным углом и координатами точек данной линии:

Источник

Суть параметрического способа уравнивания

В данном способе устанавливается связь между измеренными величинами и определяемыми.

Измеренными величинами в плановых геодезических сетях в основном являются длины линий, углы и направления. Определяемыми – координаты определяемых пунктов. В пространственных геодезических сетях GPS – измеренными являются приращения координат, а определяемыми – пространственные координаты определяемых пунктов. В нивелирных сетях измеряемыми являются приращения, а определяемыми – высоты пунктов.

Например, пусть в некоторой сети измерены длины сторон S₁, S₂,S₃,S₄ (рис. 22), известными являются координаты исходных пунктов А и В.

Определяемыми являются координаты пунктов 1 и 2. Всего четыре неизвестных: x₁, y₁,x₂, y₂. Для определения необходимо и решить следующие четыре уравнения:

В данной системе – четыре уравнения с четырьмя неизвестными, которые называются параметрами. А сами уравнения называются параметрическими. Если измерить дополнительно сторону S₅ между пунктами 1 и 2, то можно записать еще одно уравнение

Тогда получится пять параметрических уравнений с теми же четырьмя неизвестными. Система уравнений связи будет переопределена. Ей будет соответствовать множество решений. Это вызвано тем, что неизвестные величины S₁, S₂,S₃,S₄, S₅ являются результатами измерений, которые отягощены ошибками измерений. Из этого множества необходимо выбрать такое решение, которое удовлетворяет статистическим свойствам оценок: несмещенности, достаточности, эффективности.

К настоящему времени методы решения нелинейных систем уравнений разработаны недостаточно. Поэтому данные уравнения приводят к линейному виду и решение выполняют методом приближений. Линеаризованные уравнения выражаются через поправки к измеренным величинам и параметрам и называются параметрическими уравнениями поправок.

Параметрические уравнения поправок

а) Уравнение поправок сторон.

Линеаризация параметрического уравнения измеренной стороны выполняется разложением его в ряд Тейлора.

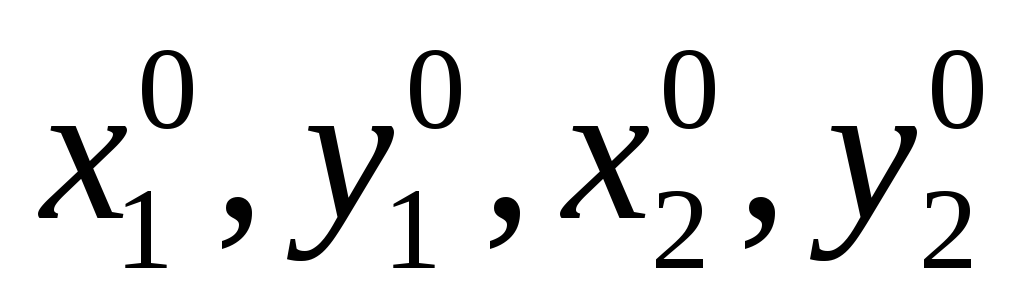
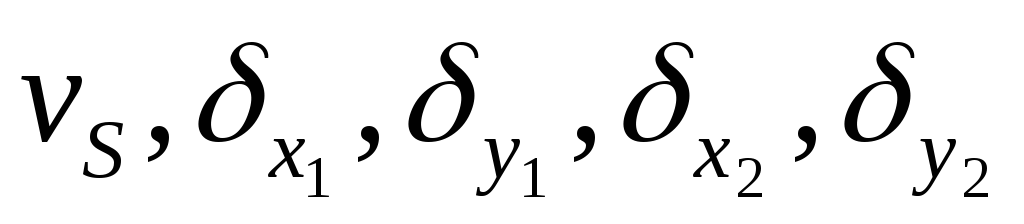
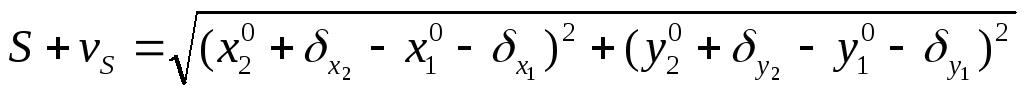
Пусть известны с определенной точностью приближенные значения координат определяемых пунктов . Они могут быть найдены по измеренным значениям линий или углов, или наперед заданными. Измеренную между ними длину стороны обозначим черезS. В результате уравнивания должны быть получены такие поправки , при которых удовлетворяется равенство

(104)

Разложение выражения, стоящего в (104) справа от знака равенства, в ряд Тейлора приводит к следующему равенству

(105)

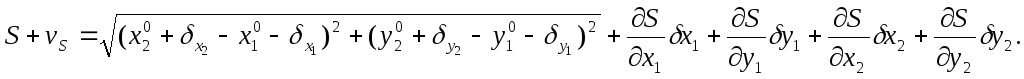
Найдем теперь частные производные

(106)

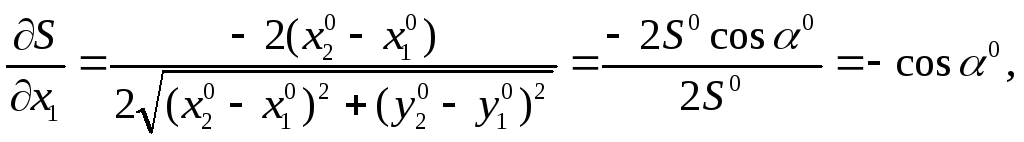
Напомним, что при разложении ряд Тейлора частные производные берутся при начальных значениях: .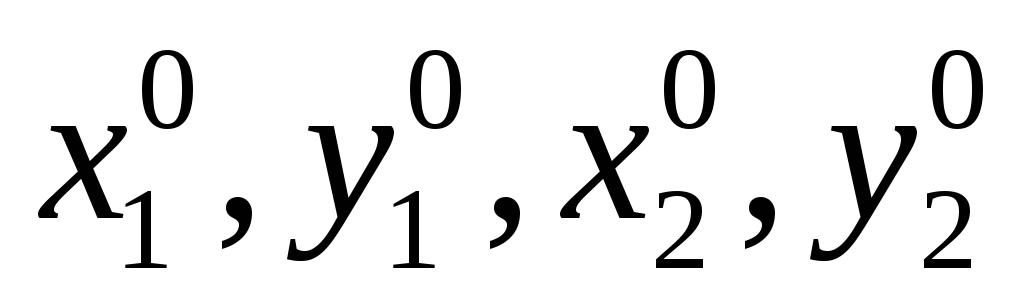

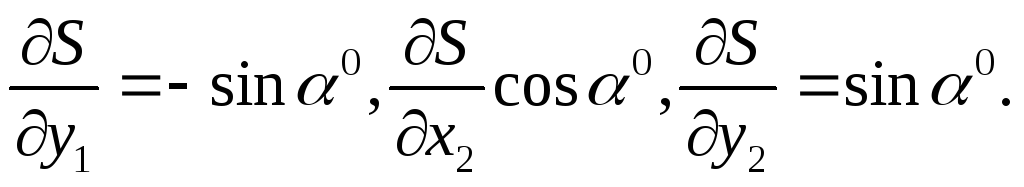
(107)

С учетом полученных выражений производных (106), (107) параметрического уравнения представим вид

(108)

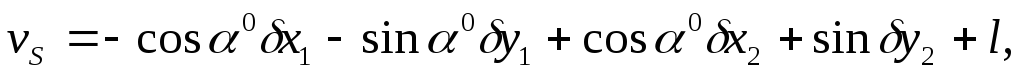
где

б) Уравнение поправок направлений.

При измерении направлений зрительной трубы теодолита наводят на точку и берут отсчет М по горизонтальному кругу. Пусть имеется n таких отсчетов на n точек: М₁, М₂,…,М_n. Назовем их измеренными направлениями.

Введем дополнительное неизвестное – дирекционный угол направления, соответствующего нулевому отсчету по лимбу. Его называют еще ориентирующим углом. Тогда дирекционные углы направлений будут:

Исходя из этих выражений можно записать, что

Для направления из точки 1 в точку 2 можно записать

(109)

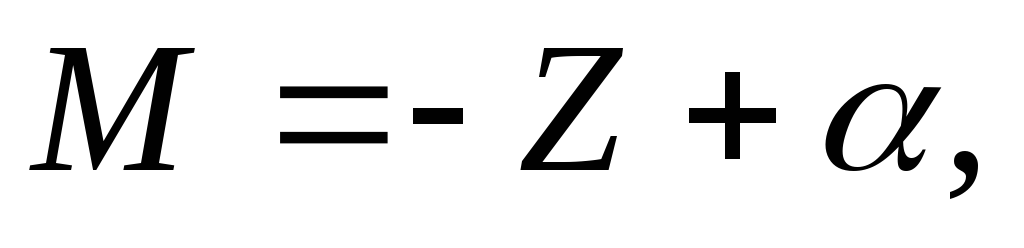
где

Из-за ошибок измерения направлений и наличия лишь приближенных координат определяемых пунктов уравнение (109) не выполняется.

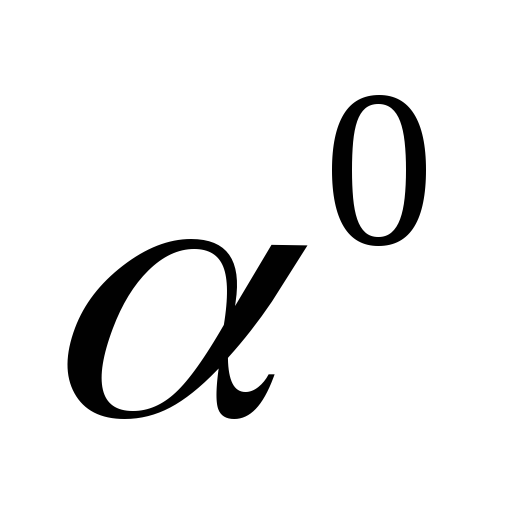
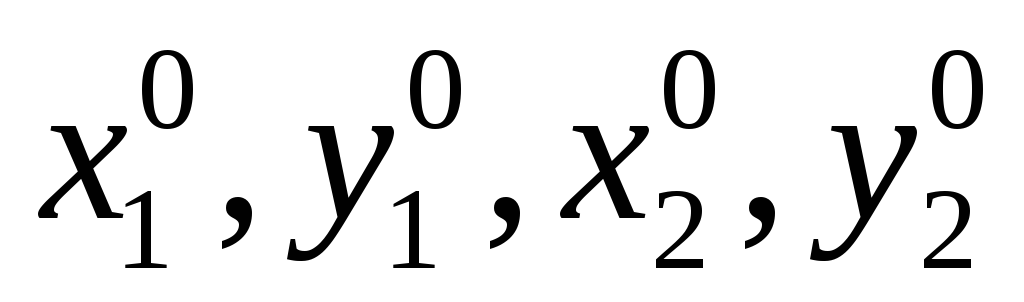
Если обозначить измеряемое направление через М, поправку в него через v, приближенное значение ориентирующего угла через Z 0 ,поправку к нему через и аналогично:– приближенное значение дирекционного угла,– поправку к нему, то можно записать:

Приближенное значение дирекционного угла вычислено по приближенным координатамопределяемых пунктов, в значения которых должны быть введены поправки.

Поправки должны быть такими, чтобы в соответствии с (109) выполнялось равенство

(110)

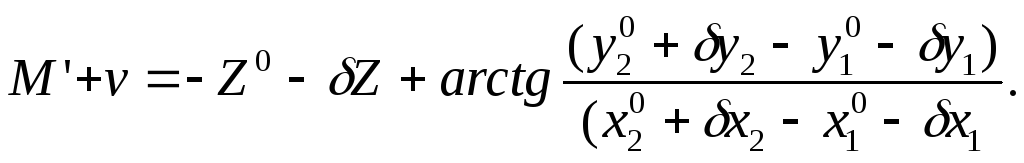
Разлагая в (110) функцию arctg в ряд Тейлора найдем

Найдем частные производные этой функции по всем параметрам

(111)

(112)

(113)

(114)

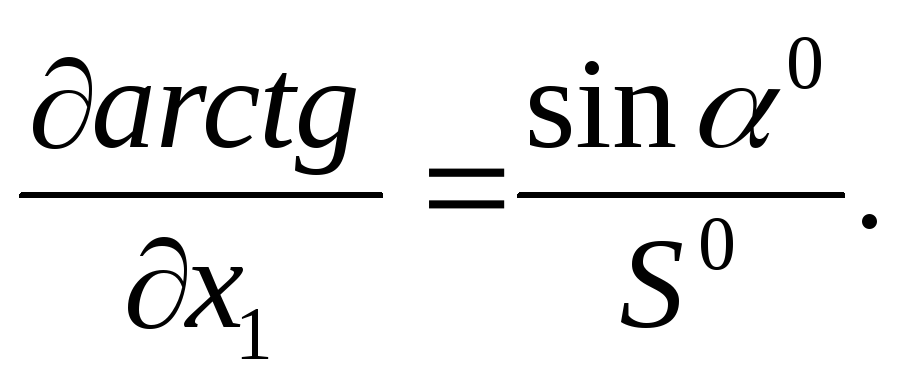
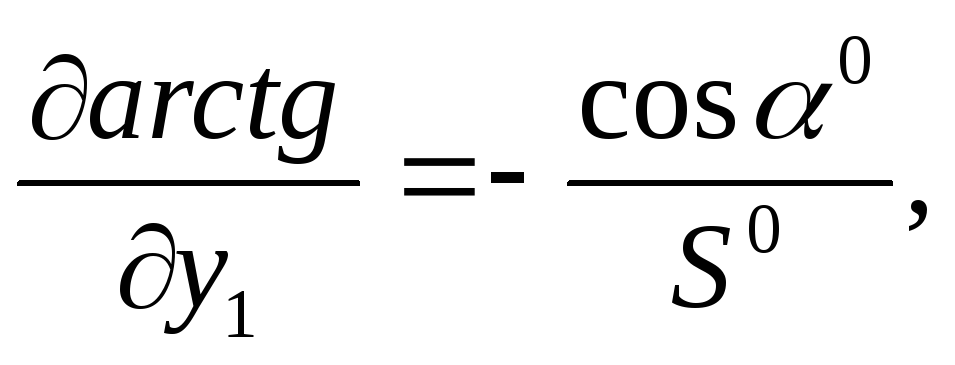
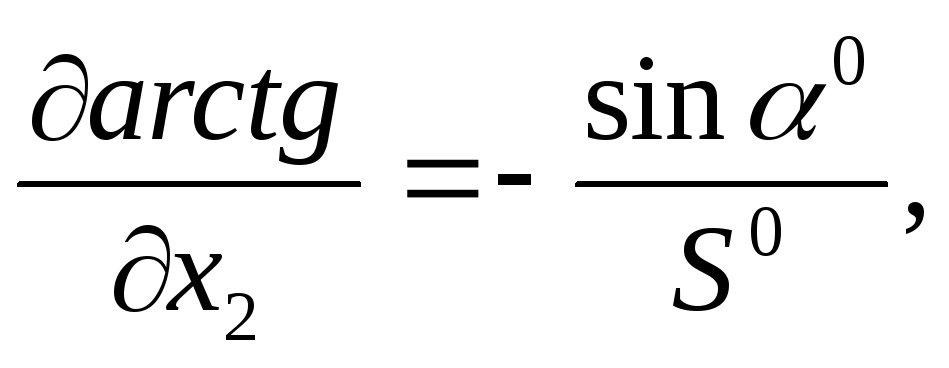
С учетом выражений для частных производных (111)-(114) параметрическое уравнивание поправок будет иметь вид

(115)

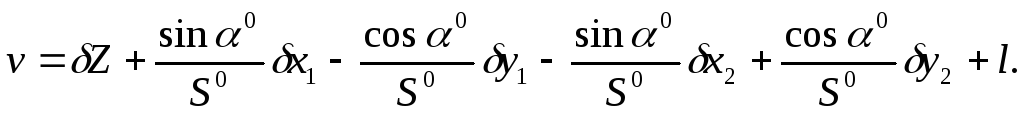
где

Если одна из точек направления является исходным пунктом, то ее координаты считают безошибочными и потому поправки в ее координаты принимают равными нулю. В том случае, если ошибками координат исходных пунктов пренебречь нельзя, выполняют уравнивание с учетом ошибок исходных данных, которое здесь не рассматривается.

в) Уравнения поправок GPS-построений.

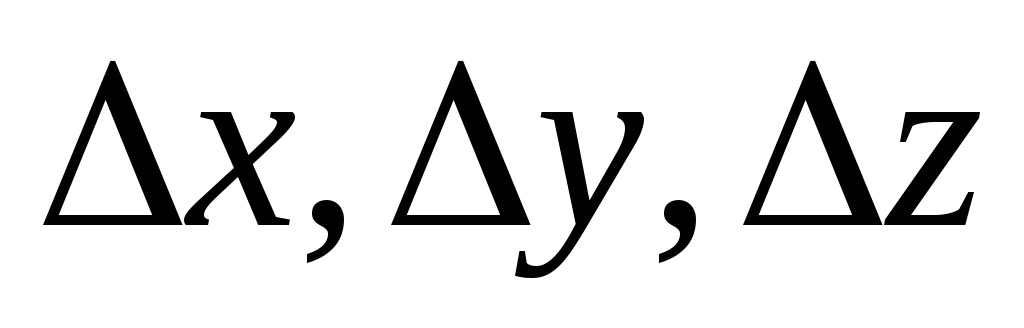
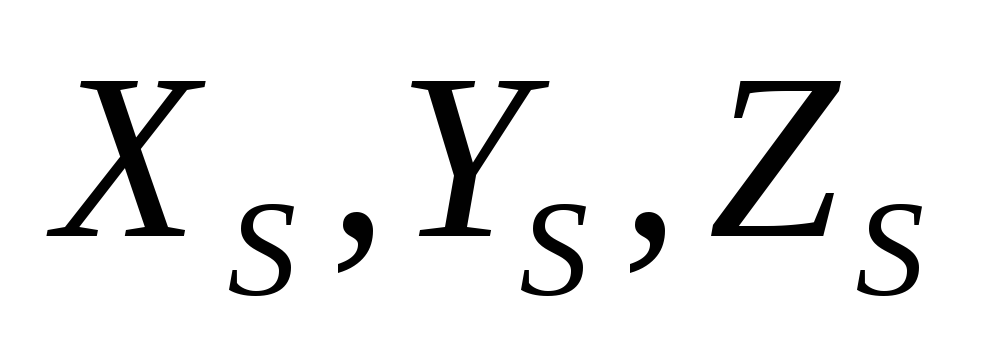
В геодезических сетях, построенных с помощью GPS, измеряются приращения координат между пунктами 1 и 2 (рис. 24) в геоцентрической системе координат. Эту систему еще называют спутниковой

Справедливы следующие очевидные равенства

где x₁, y₁,x₂, y₂ – геоцентрические координаты точек 1 и 2.

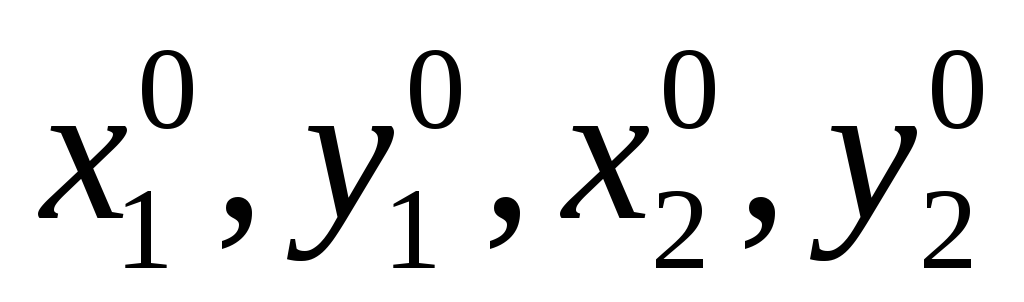
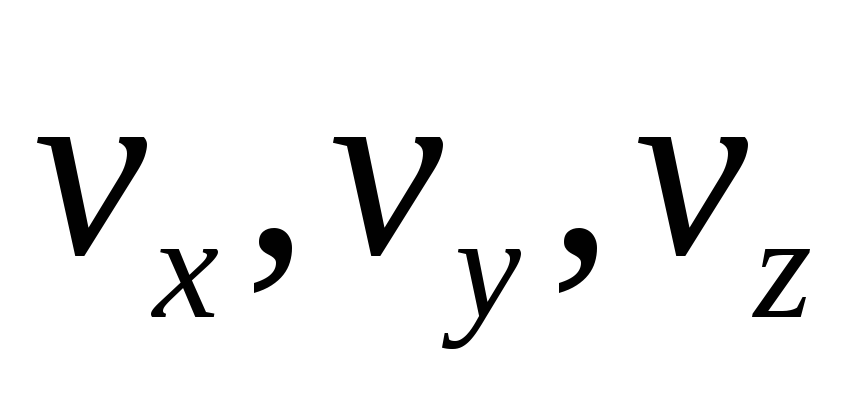
Если задаться приближенными значениями координат определяемых пунктов а поправки измеренных приращений обозначить черезсоответственно, то после уравнивания должны выполняться следующие равенства

на основе которых получают уравнения поправок

(116)

где

Следует отметить, что в геодезических сетях координаты исходных пунктов приведены в наземной системе координат, например xyz.

В этом случае по угловым и линейным элементам ориентирования их необходимо перевычислить в спутниковую систему и уравнение выполнять в этой системе. При этом элементы ориентирования могут быть заданы с определенной точностью или быть неизвестными. В последнем случае они выступают как дополнительные параметры. Если в их качестве принять углы Эйлера 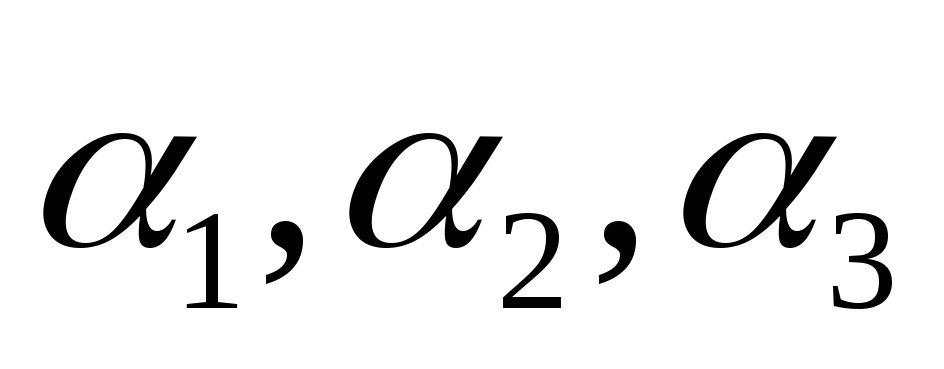и масштабный факторm то уравнение поправок в матричном виде будет таким

а – приращения координат в спутниковой системе координат, полученные по приближенным значениямуглов Эйлера и масштабного фактора– поправки в приближенные значения Эйлера и масштабного фактора.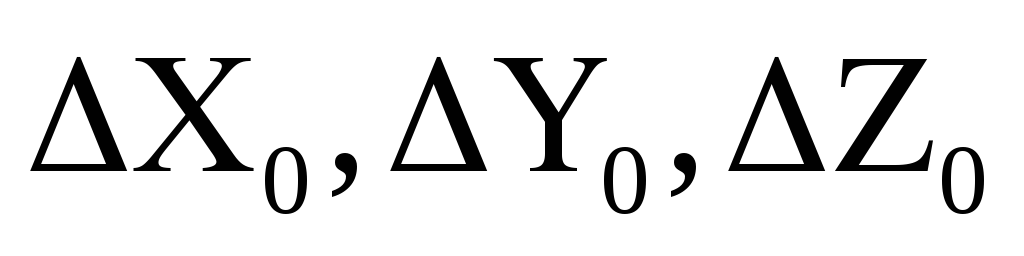

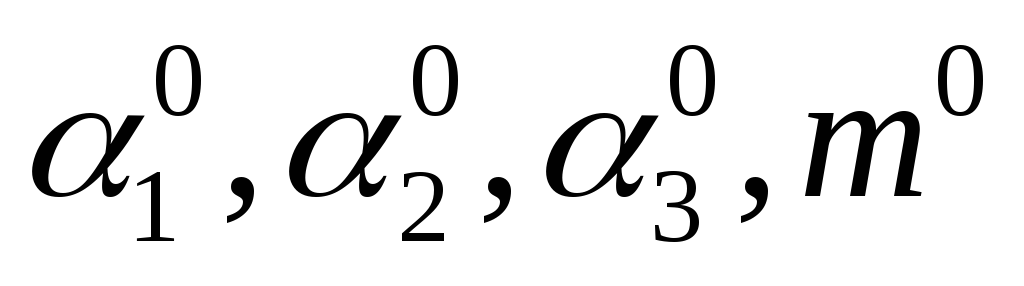
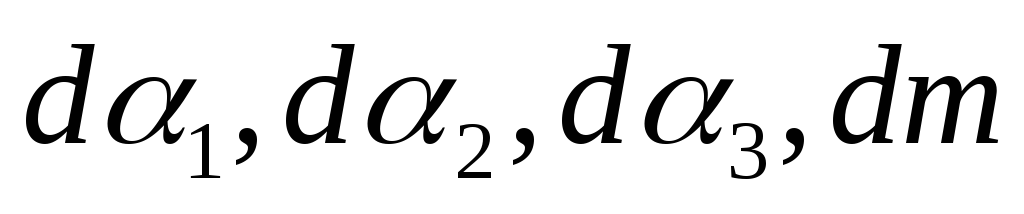
Приближенные значения координат определяемых пунктов в спутниковой системе находятся по приближенным значениям параметров и приближенным координатам этих пунктов в наземной системе координат. В данном случае перевычисляют не координаты, а приращения координат, которые используются для вычисления свободных членов.

Источник