Уравнивание полигонометрического хода параметрическим способом

4.6.4. Уравнивание системы полигонометрических ходов с одной узловой точкой

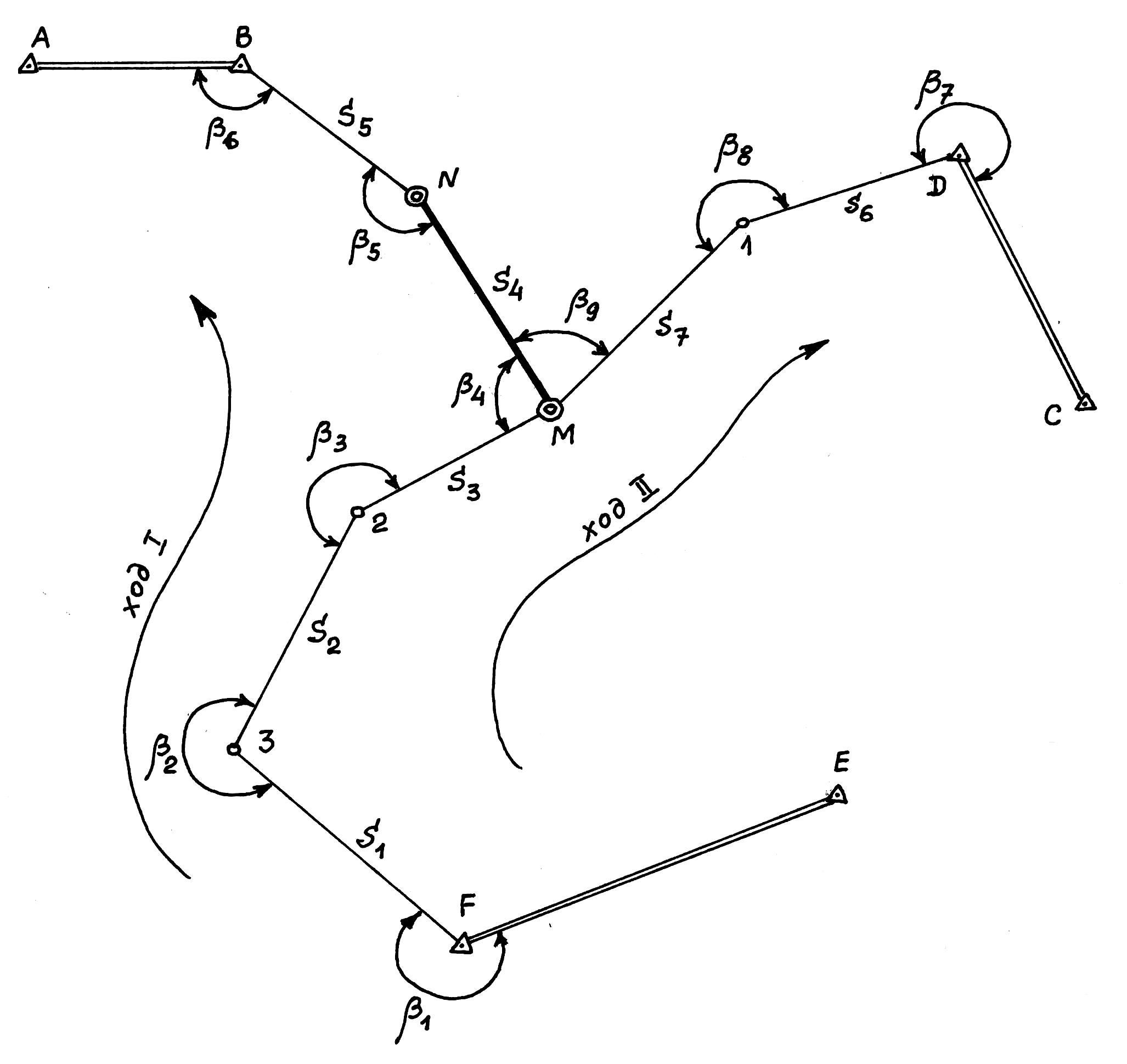
На местности между исходными линиями АВ, CD, FE проложена система полигонометрических ходов (рис. 4.10) с одной узловой точкой М: В-N—M; D-1-M; F-3-2-M. На схеме указано направление движения в полигонометрических ходах.

Координаты исходных пунктов В, D и F приведены в табл. 4.18, значения исходных дирекционных углов – в табл. 4.19, измеренных горизонтальных углов и расстояний – в табл. 4.20.

Средняя квадратическая погрешность измерения горизонтальных углов m_β = 2,0″ (измерения углов равноточные). Относительная погрешность измерения расстояний составила m_s(отн) 1:120000. Используя формулу

, (4.159)

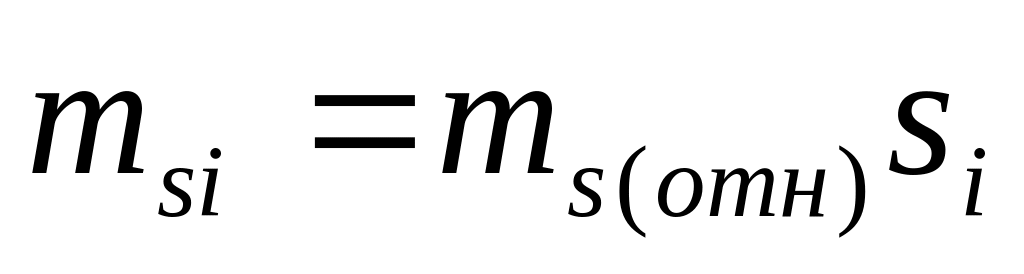
Значения весов p_i и обратных весов q_i измеренных величин в соответствии с принятой их нумерацией приведены в табл. 4.21. Значения весов получены по формулам (3.5).

Рис. 4.10. Схема полигонометрических ходов с одной узловой точкой

Источник

Беляев В.А. , Ph. D.

Система Автоматизации Геодезических работ

Уравнивание сетей полигонометрии и теодолитных ходов

Эта программа была написана мною в 1980 году для машин серии ЕС языке PL -1 и немедленно начала использоваться на предприятих Госстроя СССР и ГУГК СССР. В 1986 году вышла ее расширенная версия со строгим уравниванием для машин серии СМ на языке FORTRAN и ЕС на языке PL -1. В 1989 году программа была переписана в кооперативе «Радуга» в операционной системе MS DOS для персональных компьютеров на языке FORTRAN. С 1896 года программа работает под WINDOWS и и переведена на язык Object Pascal в среде DELPHI .

В настоящее время, и в частности, в АРМИГе полигонометрическую сеть можно уравнять как линейно-угловую без заметной потери времени на уравнивание. Однако преимущество уравнивания полигонометрической сети как полигонометрии состоит в раздельном уравнивании дирекционных углов и линий, что предоставляет существенное удобство в поиске ошибок – сперва угловых, а затем линейных. Отлаженную полигонометрическю сеть затем можно легко переуравнять как линейно-угловую и представить протокол уравнивание в формате протокола уравнивания полигонометрической сети, но с оценкой точности координат каждого пункта сети.

В институте УкрГиигис ГУГК СССР этой программой была переуравненена вся городская полигонометрическая сеть Украины и Молдавии.

Метод полигонометрии

Известные геодезические понятия, приводимые ниже, тесно связаны с правилами и логикой ввода исходных данных, поэтому приведение их с моей точки зрения не является излишним.

Полигонометрическая сеть – это сеть полигонометрических ходов между твердыми и узловыми пунктами. Полигонометрический ход — это последовательность геодезических точек на местности. На каждой из этих точек измеряется с помощью теодолита левый по ходу угол между задней и передней точками. Также измеряется расстояние между смежными точками хода светодальномером или другим мерным прибором. Твердой точкой называется точка, координаты которй не изменяются в результате уравнительных вычислений.

Узловой точкой называется конечная точка хода, которая не является твердой. Как правило, узловой точкой является точка в которой встречаются несколько ходов, однако за узловую точку может быть принята также конечная точка висячего хода с произвольным углом на этой точке.

Если первой точкой хода является твердая точка B (Рис.1), и ход направлен в направлении стрелки, то углом на этой точке является угол между другой твердой A и второй точкой хода a как передней точкой. Если точка С является конечной точкой хода, то углом на этой точке является угол между предпоследней точкой хода b как задней точкой и твердой точкой D как передней.

Если первой точкой хода является узловая точка J (Рис.2), то углом на этой точке является угол между узловым направлением и следующей по ходу точкой.

За узловое направление может быть принята любая сторона любого хода, одним из концов которой является данная узловая точка, например, направление j — e .

Если первой точкой хода является узловая точка, то углом на этой точке является угол между узловым направлением и следующей по ходу точкой. Если узловая является последней точкой хода, то углом на этой точкой является угол между предпоследней точкой и узловым направлением на данной узловой точкой.

Если на некоторой твердой точке нет направления на другую твердую точку, то в случае, когда эта твердая точка является концом только одного хода, угол на этой точке считается не измеряемым и не вводится таблицу измерений (см. ниже). Если в этой точке встречается два и более ходов, то угол на этой точке вводится в таблицу измерений, как на узловой точке.

На Рис.6 узловым направлением на твердой точке С1 является направление е-С1. Угол на твердой точке С1 в ходу 1 равен нулю, а в ходу 2 — угол еС1с.

Алгоритм уравнивания полигонометрии

Описание алгоритма уравнивания поможет пользователю правильно реагировать на сообщения программы во время процесса уравнивания.

Уравнивание полигонометрических сетей распадается на следующие этапы.

· Уравнивание сумм углов в ходах

· Уравнивание сумм приращений абсцисс

· Уравнивание сумм приращений ординат

Предполагется, что каждая узловая точка имеет три компоненты: координаты X , Y узловой точки и дирекционный угол узлового направления. Каждая из этих компонент для каждого узлового пункта принимается в качестве незвестных в процедуре уравнивания на соответствующем этапе раздельного уравнивания.

Раздельное уравнивание начинается с уравнивания дирекционных углов. На этом этапе за измеренные величины принимаются суммы углов в ходах, за неизвестные — дирекционные углы узловых направлений (вернее, поправки к предварительным значениям дирекционных углов). Предварительные значения дирекционных углов получаются простым «навешиванием» одного хода на другой. Затем вычисляются свободные члены уравнений ошибок для каждого хода как разность сумм углов и разность предварительных дирекционных углов на концах хода. Эти свободные члены выводятся в таблицу предварительных невязок. По величине этих невязок пользователь может решить – прервать уравнивание, попытаться найти ошибку или продолжить уравнивание.

Если процесс уравнивания дирекционных углов продолжен, то программа составляет нормальные уравнения – их число равно числу узлов, решает их, и в результате решения вычисляет уравненные значения дирекционных углов узлов.

На этом первый этап раздельного уравнивания завершается.

По уравненным дирекционным углам, измеренным сторонам и координатам твердых пунктов вычисляются предварительные координаты узлов также простым «навешиванием» одного хода на другой.

На втором и третьем этапе раздельного уравнивания уравниваются соответственно координаты узлов X , Y , вернее, поправки к предварительным значениям координат.

Также, как и на первом этапе вычисляются свободные члены уравнений ошибок, как разности между суммами приращений и координат и разностями координат концов ходов. Эти сободные члены – предварительные невязки по ходам – выводятся в таблицу на экран. По величине этих невязок пользователь может решить – прервать уравнивание, попытаться найти ошибку или продолжить уравнивание.

Следующий этап – это строгое уравнивание сети по теории Forstner ’ а – по методу условий с долнительными неизвестными. Неизвестными здесь являются поправки к предварительным координатам и дирекционных углов узловых пунктов. Таким образом, общее число неизвестных равно числу узлов, умноженному на три. Это обстоятельсво позволило уравнивать обширные полигонометрические сети с тысячами пунктов на таких слабых машинах как СМ, где оперативная память составляла всего лишь 64К байт.

Предварительные значения координат и дирекционных пунктов и средне-квадратические ошибки измерения углов и линий приходят из результатов раздельного уравнивания сети. Однако, средне-квадратические ошибки измерения углов и линий можно установить как опции перед началом уравнивания.

Именно проблема начальных значений средне-квадратических ошибок непосредственных измерений привела к применению итеративного уравнивания сети. На первой итерации эти значения берутся как результаты раздельного уравнивания. На следующей итерации предварительные значения координат и дирекционных углов и средне-квадратические ошибки непосредственных измерений берутся из предыдущей итерации и снова производится строгое уравнивание сети и т.д. до сходимости средне-квадратических ошибок углов и линий, либо до исчерпания установленного числа итераций.

По завершению строгого уравнивания сети программа приступает к уравниванию ходов. Хода уравниваются независимо друг от друга по методу условий. Для каждого хода составляется три условных уравнения — два условных уравнения коодинат и одно — углов. Если на одном из концов хода нет дирекционного угла, то условие углов не составляется. В результате уравнивания ходов вычисляются поправки к измеренным сторонам и углам и вычисляются окончательные координаты точек ходов.

Исходные данные

Данные, описывающие некоторую полигонометрическую сеть, распределяются в таблицах «Измерения по ходам», «Твердые пункты» и «Узлы». Дополнительные данные в виде параметров находятся на панели «Режимы».

Эти таблицы появляются на экране после открытия некоторого существующего файла, содержащего описание полигонометричекой сети. Для этого необходимо кликнуть Файл|Открыть (здесь и далее таким образом обозначается дерево меню: пункт главного меню, затем пункт в этом меню и т.д.) и в появившемся диалоговом окне выбрать нужный вам файл. При этом содержимое этого файла будет распределено по соответствующим таблицам на экране.

Если кликнуть Файл|Новый файл, то на экране появятся пустые таблицы, готовые к вводу исходных данных вручную.

Правила ввода

При вводе угловых величин необходимо придерживаться следующего:

Угол вводится в виде (символы « » не вводятся). Между градусми и минутами, минутами и секундами должен быть хотя бы один пробел. Также законно описывать угол только в градусах, например, 123.45, в градусах и минутах: 123 45.67, в градусах минутах и секундах: 122 45 59.57.

При вводе имен пунктов следует избегать применения следующих символов:

Числовые величины могут вводится как целые, числа с десятичной точкой, как числа в научном формате, например, 1 e 2 или 1.00 e 2 или 100.000.

Несоблюдение этих правил приводит к восстановлению предыдущего содержимого ячейки.

Управляющие команды

· Alt+ Del Удалить текущую строку

· F 5 вставить пустую строку ниже курсора

· Enter Ввойти в ячейку для редактирования или подтврдить ее содержимое.

· Esc Восстановить предыдущее содержимое ячейки во время редактирования.

· Alt + Backspace Отменить предудущие изменения в таблицых ( Undo ) .

· Стрелка вниз, вверх, вправо, влево, страница вверх, страница вниз — перемещение курсора по таблице.

Таблица твердых пунктов

Каждая точка в таблице Твердые пункты должна по крайней мере иметь три параметра – имя точки и координаты X и Y . Четвертый параметр – дирекционный угол может отсутствовать. Дирекционный угол можно ввести как угол или как ссылку на другой пункт в таблице, с тем, что бы он был вычислен по координатам как обратная геодезическая задача на плоскости. При этом перед именем пункта нужно ввести символ @. Ссылку на другой пункт можно ввести следующим образом. Кликните првой кнопкой мыши и в появившемся меню кликните пункт Azimuth references . Кликните в колонке дирекционных углов в таблице Твердые пункты по ячейке, в которой вы хотите вставить ссылку, а затем в колонке Имя кликните по ячейке, содержащей нужное имя пункта.

Дирекционный угол задается как направленный на пункт, которому он принадлежит, как показано стрелками на рис. 1. На пункте В твердый дирекционный угол будет иметь направление АВ, а на пункте С – направление DC .

Таблица измерений по ходам

Хода полигонометрии могут быть двух видов – обычные хода и «висячие» хода. Конечными точками обычных ходов должны быть узловые или твердые пункты. Первая и вторая точки висячего хода должны принадлежать ходу, от которого висячий ход ответвляется, и, который должен быть описан прежде описания висячего хода.

Впрочем, висячий ход можно задать и как обычный ход, включив первую и последнюю точку в число узловых, а на последней точке ввести произвольный угол, например, равный нулю.

Любой обычный ход должен иметь два начальных направления на концах. Один из них может быть пустым в случае, если этим концом является твердый пункт, на котором нет дирекционного угла, и к этому пункту примыкает только один ход.

Если конечной точкой хода является твердый пункт, то начальным направлением на этом пункте должно быть направление с этой точки на смежный твердый пункт, с которого задан дирекционный угол на данный пункт в таблице твердых пунктов.

Если конечной точкой является узловая точка, то начальным направлением должно быть узловое направление, общее для всех ходов, сходящихся в данной узловой точке. При этом на первой точке хода первым углом должен быть угол от начального направления (узлового направления) на вторую точку хода, а на последней точке хода углом должен быть угол от предпоследней точки хода на начальное направление (узловое направление) (Рис.2).

На Рис.2 J – узловая точка. Сторона Je – узловое направление. Угол, который должен быть введен на точке J , равен нулю, так как сторона Je совпадает с узловым направлением.

Узловое направление не обязательно должно совпадать с какой-нибудь стороной хода, сходящегося на данной узловой точке. За узловое направление может быть принято любое направление, исходящее из данного узла, как показано на Рис.3.

На Рис.3 углы, измеренные на узловой точке J отсчитывются от некоторого узлового направления JS .

Обычно узловыми точками сети являются такие точки, в которых сходится 3 и более ходов, как показано на Рис.2 и Рис.3. Однако любая точка сети может быть принята за узловую точку. Например, узловая точка J на Рис.4 является точкой, в

которой сходится только два хода. Угол на этой точке в ходе 1 равен нулю, а в ходе 2 – это левый угол aJb .

За узловую может также быть принята конечная точка висячего хода, как показано на Рис.5. Это другой сособ представления висячих ходов.

Для описания висячего хода в сети введите угол на точке J равный нулю. В сущности можно ввести любой угол на точке J, так его значение игнорируется программой. Он необходим только лишь для соблюдения общих правил описания ходов для избежания сообщения об ошибке.

Случай, когда конечная точка хода является твердой точкой, на которой нет дирекционного угла, распадается на два:

· На этой точке есть измеренный угол. К этой точке примыкает минимум два хода, Рис. 6.

· На этой точке угол не измерялся. К этой точке примыкает только один ход, Рис. 7.

На Рис.6 у твердой точки С1 нет дирекционного угла. Но, так как на точке С1 сходится два угла, то угол на этой точке должен быть измерен. Сторона С1е предполагается быть принята как узловое направление. Угол на этой точке в ходу 1 равен 0. Угол на этой точке в ходу 2 равен углу еС1е.

В случае, когда к твердой точке без дирекционного угла (Рис. 7) примыкает только один ход, угол на этой точке не измеряется и не вводится на соответствующей точке в таблице Измерения по ходам. Ячейка Угол на этой точке должна быть пустой.

При описании обычных ходов необходимо придеоживаться следующих правил.

· Начальные и конечные точки ходов должны быть узловыми или твердыми точками.

· На обеих конечных точках хода должен быть введен угол. Случай, когда угол не вводится, описан выше.

· На всех внутрених точках хода должны быть углы.

· На всех точках, кроме последней, должны быть введены расстояния. Расстояние предполагается между текущей и следующей точкой. Если расстояние на некоторой точке не вводится, то эта точка считается конечной точкой хода.

Висячие хода — это хода, исходящие из некоторой точки родительского хода и заканчиваются точкой, которая не является ни узловой, ни твердой точкой (Рис. 8).

При вводе висячих ходов нужно иметь ввиду

· Первая и вторая точка хода должны быть общими с точками родительского хода. На Рис. 8 висячий ход проходит через точки a , b , v 1, v 2, v 3 . Точки a и b – общие с точками родительского хода.

· Угол и сторона на первой точке висячего хода должны оставаться пустыми.

· Последняя точка не должна быть ни узловой ни твердой.

Формат исходных данных.

Исходные данные для уравнивания полигонометрических сетей могут храниться в двоичном или ASCII (текстовом) форматах. Если вы кликните Файл| Сохранить, то содержимое таблиц будет сохранено в двоичном формате. Если при последующем прогоне эти данные окажутся синтаксически корректными, то файл будет переписан в ASCII формат. Это свойство программы позволяет вам прервать ввод в любом месте, сохранить данные в двоичном формате и затем продолжить ввод на следующей сессии.

В обоих форматах файлы имеют умалчиваемое расширение . pol .

Как правило, нет необходимости готовить данные в виде текстового файла. Полигонометрическая сеть формируется автоматически из Редактора Полевых Данных, который, в свою очередь, как правило, заполняется автоматически из полевых регистраторов, или из Редактора уравнивания линейно-угловых сетей, куда данные поступают из Редактора Полевых Данных.

Данные в ASCII формате могут быть подготовлены в любом текстовом редакторе.

Данные, описывающее полигонометрическую сеть распадаются на блоки, записи, подзаписи и слова. Блоки должны заканчиваться символом «/», записи — символом

«)», подзаписи – символом «>». Слова отделяются друг от друга как минимум одним пробелом. Блок содержит одну или более записей, запись содержит одну или несколько подзаписей, подзапись содержит одно или более слов.

Последлвательность нескольких разделителей можно заменить одним старшим. Например, последовательность “>)/” можно заменить символом «/».

Исходные данные, описывающие полигонометрическую сеть, можно представить в виде следующей диаграммы.

Прямоугольники Опции и Твердые и узловые пункты представляются каждый в виде одного блока. Хода представляются в виде набора блоков. Каждый ход описывается одним блоком. Одно соединение означает, что старший прямоугольник порождает один младший, два соединения – много младших.

Опции содержат одну подзапись. Словами в этой подзаписи являются режимы уравнивания, представленные ключевыми параметрами. Класс сети представляется ключевым параметров k = n , где k – ключевое слово, n – его значение: 1 или 2 или 3 иди 4 или 5. Умалчиваемой значение для класса сети равно 5. Параметр класса сети и спользутся для установления допустимых значений невязок в ходах и средне-квадратических ошибок непосредственных измерений в соответствии со следующей таблицей.

Число итераций представляется ключевым параметром it = n , где it – ключевой слово, а n – число итераций. В случае, если в сети нет узлов, этот параметр игнорируется.

В БД – записать в базу данных. Представляется ключевым параметром db = y или db = n , в зависимости включен или выключен Check box .

Угл. ско и Лин. ско задают средне-квадратические ошибки измерения углов и линий соответственно, и представляются ключевыми параметрами mb = , ms = . Эти величины используются только на этапе строгого уравнивания. В случае, если эти величины заданы, то они будут использованы для вычисления начальных значений весов ходов, в противном случае эти величины будут взяты из результатов раздельного уравнивания.

Строгий способ уравнивания. Задается ключевым параметром su = y / n . Если параметр включен, то после завершения раздельного уравнивания будет произведено строгое уравнивание сети.

Три радио-кнопки Мерные устройства, Светодальномер, Оптический дальномер – определяют соответственно метод измерения линий – стальными мерными приборвми (лентами, рулетками, проволоками), оптическим дальномером и светодальномером. Представляются ключевым параметром miz = .

QReport . Если этот Check box включен то результаты уравнивания будут выведены в формате QUICK REPORT.

Блок 2 . (Твердые и узловые пункты). Данные этого блока размещаются в таблицах Твердые пункты и Узлы. В исходном файле данные этого блока задаются следующими записями.

· Имена твердых пунктов . Каждое имя задается в виде слова.

· Имена узловых пунктов . Каждое имя задается в виде слова.

· Координаты твердых пунктов . Каждая координата задается в виде слова. Каждая пара координат задается в виде подзаписи.

· Диреккционные углы . Каждый угол задается в виде подзаписи. Если угол отсутствует, то он задается пустой подзаписью в виде двух символов >>. Дирекционный угол может быть задан в виде ссылки на другой твердый пункт, например, @ , который описан прежде текущего.

Блок 3. Описание ходов. Данные этого блока размещаются в таблице Измерения по ходам. В исходном файле данные этого блока задаются следующими записями.

· Имена точек хода . Каждое имя задается в виде слова.

· Горизонтальные углы . Каждый угол задается в виде подзаписи. Число углов должно быть равным числу точек Если первый или последний угол не наблюдался, то он вводится в виде пустой подзаписи.

· Стороны хода . Каждая сторона задается в виде слова.

При описании висячего хода первая и вторая его точки должны быть точками родительского хода. Число углов и сторон должно быть равными числу точек хода минус 2. Первый угол должен относиться ко второй точке хода, а на последней точке хода угол не задается. Первая измеренная сторона должна быть между второй и третьей точками хода.

Ниже приведен фрагмент описания некоторй полигонометрической сети. Информация в строке после символа точка с запятой является комментарием и программой ввода игнорируется.

k=5 it=1 l=2 su=y db=y/ ; опции

P 20300 P 21500 P 20800 P 21000) ; имена твердых пунктов

T 111 T 213 T 206) ; имена узловых пунктов

788.680 569.840>808.891 494.911>

875.239 245.004>849.849 321.022) ; координаты твердых пунктов

@ P 21500>@ P 20300>@ P 21000>@ P 20800/ ; дирекционные углы в виде ссылок

P 20300 T 202 T 201 T 109

T 110 T 111); имена точек хода

90 28 30>177 19 24>179 39 30>86 29 12>

169 50 30>0 0 0); углы

45.490 45.930 72.570 92.330

P 20300 T 204 T 205 T 402

268 35 0>191 28 48>249 1 30>187 4 0>

49.260 61.900 122.190 106.120 /

P 21500 T 214 T 213)

242 29 30>105 38 0>0 0 0)

Главное меню

С помощью главного меню производятся следующие операции: чтение исходных данных, запуск задачи уравнивания, проверка корректности содержимого таблиц, поиск, операции с базой данных, преобразование полигонометрии в линейно-угловую сеть, печать протокола уравнивания и т.д.

Пункты главного меню .

· Файл. Этот пункт имеет следующие подпункты.

· Открыть . Открывается диалоговое окно и в нем существуюшие файлы с расширением . pol . Выберите нужный вам файл, и его содержимое появится в таблицах и опциях.

· Новый файл . В диалоговом окне введите имя файла, которое станет текущим для данных, вводимых вручную. После возвращения из диалогового окна перед вами появятся пустые таблицы и опции, готовые для ручного ввода.

· Сохранить . Этой командой содержимое таблиц и опций сохраняется в двоичном формате (вы не можете видеть содержимое двоичного файла в текстовом редакторе) под текущим именем . Если вы захотите прогнать этот файл, и он окажется синтаксически корректным, то он будет переформатирован в текстовый формат (вы сможете его увидеть в текстовом редакторе).

· Сохранить под другим именем . Этой командой содержимое таблиц и опций сохраняется в двоичном формате под новым именем, которое вы назначаете в диалоговом окне. Это имя становится текущим.

· Найти . Вы можете найти имя пункта или ход по его номеру, кликнув соответствующий пункт меню. Появляется диалоговое окно, в которое вы вводите имя пункта или номер хода.

· Начать уравнивание .Этой командой начинается синтаксическая проверка содержимого таблиц. И в случае отсутствия ошибок начинается процесс уравнивания.

· Проверить . Производится синтаксическая проверка без уравнивания.

· База данных .С помощью пунктов подменю этого пункта вы можете сделать следующее.

· Создать или очистить базу данных в текущей директории.

· Координаты твердых пунктов . При вводе твердых пунктов вы сможете вводить только имена твердых пунктов. Координаты пунктов будут считываться из базы данных и копироваться в соответствующие ячейки.

· Редактор базы данных .Появляется таблица с содержимым базы данных.

· Линейно- угловая сеть. Текущая полигонометрическая сеть переформатируется в линейно-угловую сеть. Запускается программа уравнивания линейно-угловых сетей. Уравненная линейно-угловая сеть снова переформатируется в полигонометрическую сеть, Протокол уравнивания формируется в формате полигонометрической сети, но с оценкой точности каждой точки сети. При уравнивании полигонометрии получаем оценку точности положения только узловых пунктов.

Читайте также:  Способы кодирования информации доклад для 5 класса

· Уравнять . Для превращения текущей сети в линейно-угловую сеть необходимо прогнать уравнивание в режиме с базой данных, так как данные для уравнивания линейно-угловой сети формируются из базы данных. Файл, представляющий полигонометрическую сеть в виде линейно-угловой сети, всегда имеет имя utb . tri .

· Снова превратить в сеть полигонометрии . Результаты уравнивания линейно-угловой сети utb . tri считывются из базы данных и переформатируются в протокол уравнивания полигонометрии в файле utb . lst .

· Протоколы . Пункты подменю этого пункта выводят в текстовый редактор, кроме протокола уравнвания в формате Quick Report , следующую информацию.

· Средние из полевого журнала . Если сеть сформировалась из Редактора Полевых Данных, то каждый угол и сторона из каждой станции формируются как средние из наблюдений на ту же самую точку. В файл average . lst выводятся наблюдения, средние из наблюдений и отклонения от средних. Кроме того выводятся средние из измерений сторон со смежных станций. По отклонениям от средних можно получить первое впечатление о качестве непосредственных измерений

· Анализ наблюдений на твердых пунктах . Если сеть сформировалась из Редактора Полевых Данных, то в файл cObserv . lst выводятся результаты сравнения между измеренными с твердых пунктов на твердые направления и стороны и этими же величинами, вычисленными по координатам соответствующих пунктов. По результатам такого сравнения можно сделать вывод о точности измерений или о правильности координат твердых пунктов.

· Протокол уравнвания в формате Quick Report . . этот пункт становится активным, если перед началом уравнивания установить в режимах опцию QReport .

· Протокол уравнивания в файле pol . lst . Протокол уравнивания выводится в текстовый редактор.

· Исходный файл линейно угловой сети utb . tri . В текстовый редактор выводится файл линейно-угловой сети, полученный из данной полигонометрической сети.

· Протокол уравнивания линейно-угловой сети utb . lst . В текстовый редактор выводится протокол уравнивания линейно-угловой сети в формате полигонометрической сети.

· Исходный файл полигонометрической сети . Исходный файл данной полигонометрической сети, если он в текстовом формате, выводится в текстовый редактор.

Предварительные угловые невязки

Таблица предварительных угловых невязок в ходах – это в сущности представление матрицы уравнений ошибок, свободные члены которых – это предварительные угловые невязки в ходах. Величины этих невязок не обязательно соответствуют угловым ошибкам в ходах, так как предварительная невязка в некотором ходе может «прийти» из другого хода во время вычисления предварительных величин дирекционных углов. По величине угловых невязок можно сделать вывод о наличии или отсутствии грубых угловых ошибок в ходах как результат наблюдений или ошибок в координатах твердых пугктов. Однако, если только в одном ходу появилась грубая невязка, то именно в этом ходу следует искать грубые ошибки в угловых измерениях.

Идея поиска хода с грубой ошибкой состоит в вычислении невязок полигонов, имеющих общий ход. Если, например, окажется, что в некотором «большом» полигоне нет грубой угловой невязки, а в каждом из двух «малых» полигонов, из которых состоит большой полигон, есть грубые невязки, то вероятнее всего ошибка находится в «перемычке» — в ходах, являющимися общими для двух малых полигонов.

Вы можете ввести список ходов, составляющих полигон, в редактирующее окно под таблицей невязок; номера ходов отделяются друг от друга хотя бы одним пробелом, либо путем двойного клика по номеру хода в таблице перенести номер хода в редактирующее окно. Номера ходов должны располагаться в порядке их следования в полигоне.

По завершении ввода номеров ходов кликнине по кнопке Невязки, и в окне MESSAGE появится величина невяки в ходу в минутах.

Если сеть состоит из одного или нескольких независимых ходов с заданными дирекционными углами на концах этих ходов, то при увереннсти отсутствия грубых ошибок в сторонах, можно попытаться локализовать грубую угловую ошибку в ходу.

Для этого кликните по кнопке Ошибка. В появившемся окне установите номер хода стрелкой вверх и кликните OK . В столбце Вероятный угол появится вероятное значение угла на точке в столбце Имя. Теперь вы можете заменить измеренный угол на вероятный и снова запустить уравнивание.

Предварительные линейные невязки

После уравнивания дирекционных углов узловых пунктов программа выполняет уравнивание координат X и Y узлов. За измеренные величины принимаются суммы приращений координат ходов. По суммам приращений координат вычисляются предварительные координаты узлов и свободные члены уравнений ошибок, как разности между предварительными координатами концов узлов и «измеренными» суммами приращений координат. В результате снова получаем окно предварительных невязок, по которым можно принять решение – продолжить уравнивание, прекратить уравнивание или в случае грубых ошибок попытаться локализовать ошибку. Если удалось найти ход, содержащий ошибку, то можно попытаться найти ошибочную линию.

Алгоритм поиска хода с грубой линейной ошибкой также, как и в случае уравнивания дирекционных углов, основан на сравнении невязок в полигонах.

Алгоритм поиска линии с грубой ошибкой основан на выборе линии, для которой вектор ошибки хода совпадает по направлению с вектором линии. Разумеется такой метод эффективен в случае только одной грубой линейной ошибки в ходу.

Строгое уравнивание сети

Если раздельное уравнивание сети завершилось благополучно, то программа переходит к строгому уравниванию по методу Ферстнера. Исходными данными для уравнивания являются суммы «измеренных» углов и приращений координат по ходам, уравненные на раздельном этапе дирекционные углы и координыты узловых пунктов, а также средне-квадратические ошибки измерения углов и линий.

В результате уравнивания вычисляются уравненные значения координат и дирекционных углов узловых пунктов, поправки в измеренные углы и линии, а также новые значения средне-квадратической ошибки измерения линий. Средне-квадратическая ошибка измерения углов не изменяется в процессе уравнивания, так как считается, что она определена достаточно надежно на этапе уравнивания дирекционных углов.

С эими новыми значениями и параметрами программа готова приступить к следующей итерации и т.д. до сходимости средне-квадратической ошибки измерения линий, либо до исчерпания числа итераций, заданных в опциях.

Случай сети без угловых привязок на твердых пунктах

В этом случае раздельное уравнивание сети производится дважды. Сперва все твердые пункты, кроме первого, переводятся в разряд узловых. Исходный дирекционный угол на первом твердом пункте принимается равным нулю. Таким образом, уравненные координаты после первого этапа уравнивания получаются развернутыми вокруг первого на угол, равный истинному значению дирекционного угла на этом пункте, который покамест нам не известен.

Для определения этого угла производится вычисление параметров преобразования координат по Гельмерту из старой системы координат, полученной на первом этапе, в новую систему, определяемую координами твердых пунктов сети.

Если задача Гельмерта завершается благополучно, то производится второй этап раздельного уравнивания, при этом за дирекционный угол на первом твердом пункте принимается угол поворота новой системы координат относительно старой.

Осбенность преобразования координат по Гельмерту состоит в необходимости достаточно точного определения начальных значений параметров преобразования. В противном случае итеративная процедура не сойдется.

Перед началом итераций вычисляются четыре параметра преобразования для пар точек с порядковыми номерами 1 и 2, 1 и 3, 1 и 4 и т.д., которые выводятся на экран в виде таблицы. Если для некоторой пары или все пары дают различные значения параметров, то это указывает на некорректность исходных данных для задачи Гельмерта – в нашем случае несоответствие координат твердых пунктов в условной и истинной системах координат. В этом случае лучше всего прервать уравнивание, нажав кнопку Выход. Если продолжить уравнивание, нажав кнопку Дальше, то получим остаточные невязки после завершения итераций Гельмерта в виде следующей таблицы.

Протокол уравнивания

Результаты уравнивания выдаются либо в тектовый файл pol . lst в текущей директории, либо в формате Quick Report , как показано ниже.

Автор выражает признательность работникам киевских институтов УкрГиигис и УкрГиинтиз за участие в отладке программы, без чего ее промышленное использование оказалось бы невозможным.

1. Forstner. Ausgleichung und Genauigkeit von Polygonzugen im weitmaschigen Dreiecksnetz. Stuttgart . 1933.

2. Антонюженко В.Ф. Уравновешивание полигонометрических сетей. Геодезиздат, 1962.

Источник