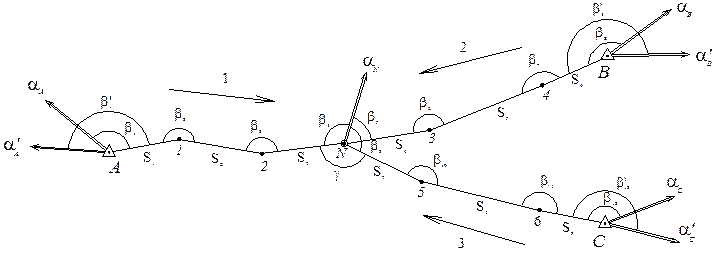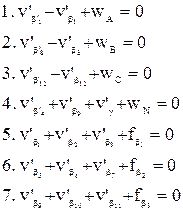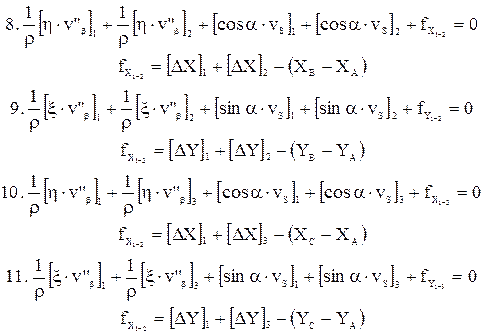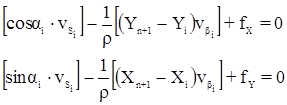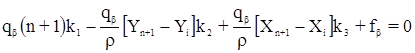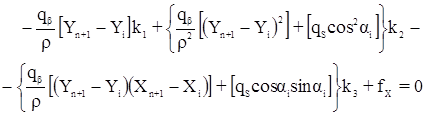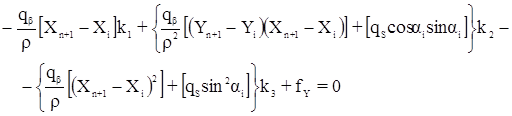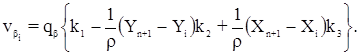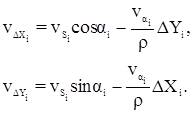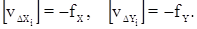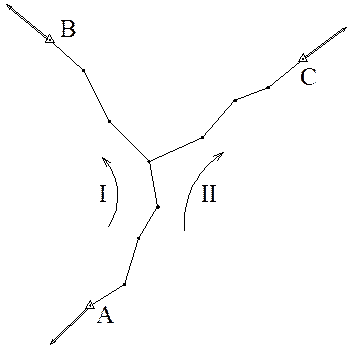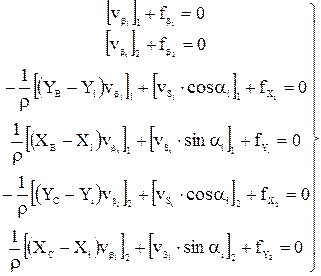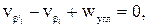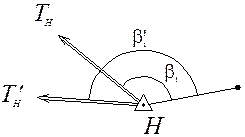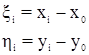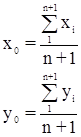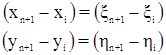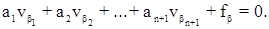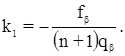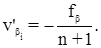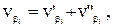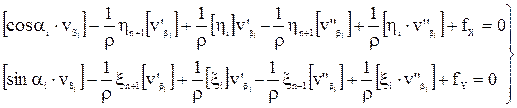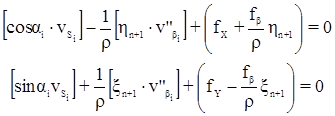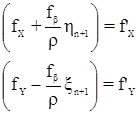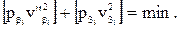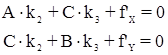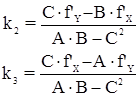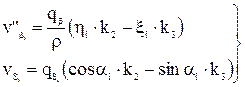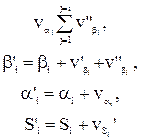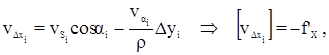Уравнивание полигонометрического хода любой формы двухгрупповым коррелатным способом

Уравнивание полигонометрической сети двухгрупповым коррелатным способом

При наличии исходных дирекционных углов на узловых пунктах, а также при измерении по два примычных угла в исходных пунктах целесообразно применение двухгруппового способа уравнивания. В этом случае вводятся центральные координаты , соединяющего для каждого хода сети, соединяющего узловые пункты с исходными (рис. 20.3). например, в данной сети измерено 16 углов и 9 линий для определения положения 7 новых пунктов полигонометрии, т.е. число избыточных измерений составляет:

R = (16 + 9) – (7·2) = 11,

r_α = N + T + Q – 1 = 0 + 3 + 1 – 1 = 3,

r_X,Y = (N + T – 1)·2 = (0 + 3 – 1)·2 = 4,

Рисунок 20.3 – Схема сети

При этом в 7 уравнениях дирекционных углов, примычных углов и горизонта все коэффициенты равны ±1. Эти уравнения включаются в 1-ю группу и решаются совместно. А затем решаются 4 преобразованные условные уравнения координат.

Рассмотрим вид этих условных уравнений поправок:

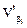
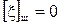
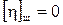
Невязки f_X и f_Y вычислены после предварительного исправления углов введением первичных поправок ; — центральные координаты для каждого хода, т.е. и . Если в полигонометрической сети возникают только уравнения 5-11 (т.е. нет условия горизонта и углов) , то каждое из угловых уравнений (5, 6, 7) решается отдельно, а затем совместно решаются четыре условных уравнения координат (8-11). В остальном ход уравнивания и оценки точности не отличается от уравнивания одиночного хода.

Дата добавления: 2016-06-02 ; просмотров: 1169 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Уравнивание коррелатным способом хода, опирающегося на исходные пункты и направления

Рассмотрим схему хода (рис. 19.1). В таком ходе общее измерение составляет п – линий и п + 1 углов, т.е. всего (2п + 1) измерений. Количество необходимых измерений составляет 2(п – 1). следовательно, число избыточных измерений r = (2n + 1) — 2(п – 1) = 3.

Рисунок 19.1 – Схема полигонометрического хода

Возникают три условных уравнения поправок:

Эти уравнения имеют вид:

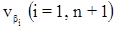
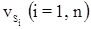
где – поправки в измеренные углы;

– поправки в измеренные длины линий;

X_i, Y_i (i = Нач, 1,2, …, n-1, Кон) – координаты текущей точки хода, в которой измерен угол b_i;

X_n, Y_n – координаты конечной точки хода.

При этом a_i, f_X, f_Y вычисляются без предварительного распределения угловой невязки. Для упрощения вычислений координаты пунктов полигонометрии могут вычисляться в условной системе, когда координаты начального пункта приравниваются к нулю.

Система нормальных уравнений коррелат имеет вид:

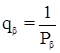
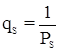
Здесь — обратный вес измеренных углов, — обратные веса измеренных длин линий. В результате решения нормальных уравнений определяют коррелаты k₁, k₂ и k₃. Поправки в измеренные углы вычисляются по формуле:

Контроль: .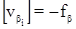

Поправки в измеренные длины линий вычисляются по формуле:

.

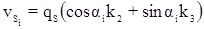
Поправки в предварительные значения дирекционных углов вычисляются по формуле:

.

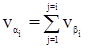
Уравненные углы, дирекционные углы и длины линий находят введением поправок v_b, v_a и v_S в значения b, a и S. Уравненные значения приращений координат вычисляют по уравненным дирекционным углам и длинам линий:

.

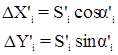
Кроме того, поправки в приращения координат можно вычислить по формуле:

Контроль:

В этом случае уравненные приращения координат вычисляются по формулам:

.

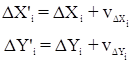
Уравненные координаты пунктов полигонометрического хода вычисляются по формулам:

Источник

Уравнивание полигонометрической сети коррелатным способом

Число условий, возникающих в сети, определяется по формуле:

где N – число замкнутых полигонов;

Т – число исходных пунктов в сети.

Если на узловых пунктах были измерены (определены по астрономическим или гироскопическим наблюдениям) дирекционные углы, то:

где Q – количество измеренных дирекционных углов в узловых пунктах.

Из всех условий будем иметь r_α условий дирекционных углов и r_X,Y условий координат. Кроме того, в сети могут возникать условия горизонта и твердого угла. Для составления условных уравнений поправок по схеме сети намечают замкнутые и разомкнутые полигоны, опирающиеся на исходные пункты. При этом все полигоны должны быть независимыми и все ходы должны быть включены в полигоны. Намеченные полигоны нумеруют, а их направление показывают стрелкой (рис.20.1).

Рисунок 20.1 – Схема полигонометрической сети

т.е. в такой системе 6 условных уравнений, из которых 2 – дирекционных углов и 4 – координат.

Эти уравнения имеют вид:

Если в сети измерялись по два примычных угла в исходных пунктах (рис. 20.2), то условные уравнения поправок угла имеют вид:

Рисунок 20.2 – Схема примыкания к двум пунктам

Эти условия необходимо составлять не только для контроля, но и включать их в уравнивание, т.к. это повышает вес уравненных элементов сети. Аналогично поступают с условием горизонта, когда в узловом пункте измерены не только необходимые углы, но и углы, замыкающие горизонт.

От условных уравнений в соответствии с принципом наименьших квадратов переходят к системе нормальных уравнений коррелат, число которых равно числу условий. По найденным из решения нормальных уравнений коррелатам определяют поправки в углы и длины линий. Дальнейший процесс уравнивания и оценки точности полигонометрической сети такой же, как и при уравнивании отдельного полигонометрического хода.

Дата добавления: 2016-06-02 ; просмотров: 1366 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Двухгрупповое уравнивание полигонометрии

Введем в исходную систему условных уравнений (20.1) центральные координаты:

где х₀ и у₀ – координаты центра тяжести хода, вычисляемые по формулам:

При этом 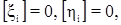т.к. ξ_i и η_i представляют собой уклонения отдельных значений от среднего арифметического из них. Вычисление центральных координат по сути соответствует параллельному переносу системы координат, поэтому:

С учетом центральных координат исходная система условных уравнений примет вид:

(19.2)

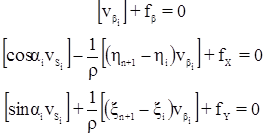
Полученную систему условных уравнений разделим на две группы:

в I группу отнесем условное уравнение поправок дирекционных углов:

;

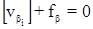
во II группу отнесем условные уравнения поправок абсцисс и ординат.

В общем виде условное уравнение поправок дирекционных углов можно записать в виде:

Этому условному уравнению будет соответствовать одно нормальное уравнение коррелат вида:

Учитывая, что a₁ = a₂ = … = 1 и 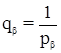, получаем:

В коррелатное уравнение поправок 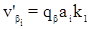подставим значения a_i и k_i:

Таким образом, первичные поправки в углы равны невязке с обратным знаком, деленной на количество углов. Полная поправка в измеренные углы будет равна:

где 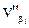— вторичные поправки в углы.

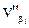
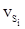
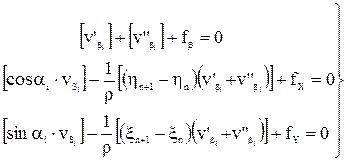
Для определения вторичных поправок в углы и одновременно поправок в длины линий надо совместно решить систему условных уравнений поправок:

.

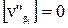
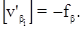
Из первого уравнения следует, что , т.к. Раскроем круглые скобки во втором и третьем уравнениях:

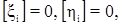
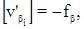
Учитывая, что получим:

В полученных уравнениях

являются преобразованными свободными членами, которые равны невязкам в приращениях координат, вычисленных после введения в измеренные углы первичных поправок. Окончательно получим систему преобразованных условных уравнений поправок:

которую необходимо решить при условии:

Этой системе условных уравнений соответствует система трех нормальных уравнений коррелат с тремя неизвестными коррелатами – k₁, k₂ и k₃:

.

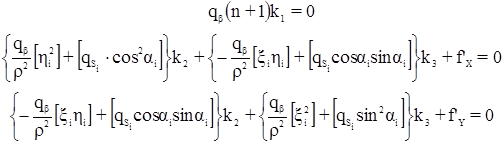
При этом нормальные уравнения разделились на две независимые группы, т.к. коррелата k₁ входит только в первое уравнение, а k₂ и k₃ – только во второе и третье. Из первого уравнения следует, что k₁ = 0, т.к. q_β ≠ 0 и (n + 1) ≠ 0. Обозначим коэффициенты во втором и третьем уравнениях через А, В и С. Тогда:

Вторичные поправки в углы и поправки в длины сторон вычисляются по формулам:

Остальные вычисления выполняются аналогично коррелатному уравниванию:

,

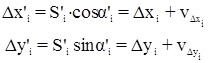
где

Источник