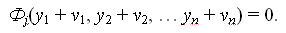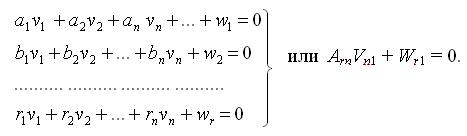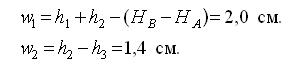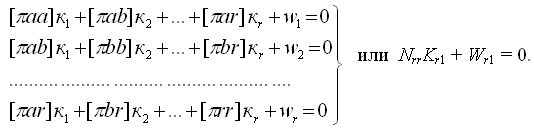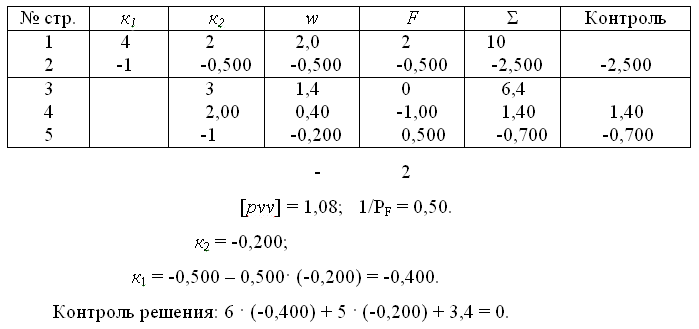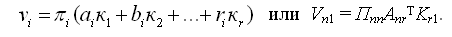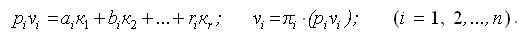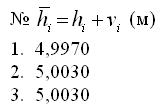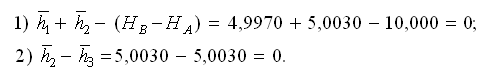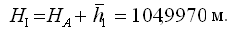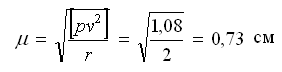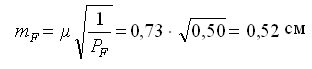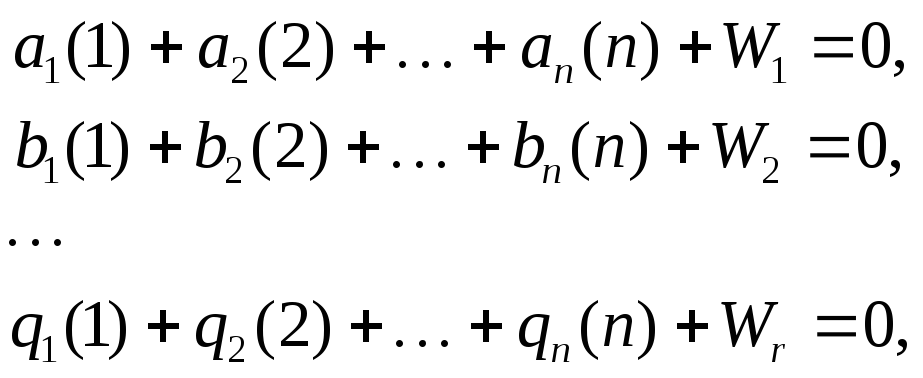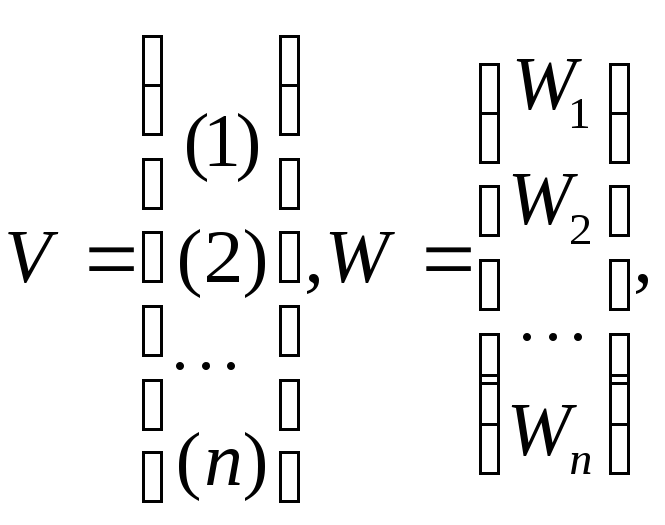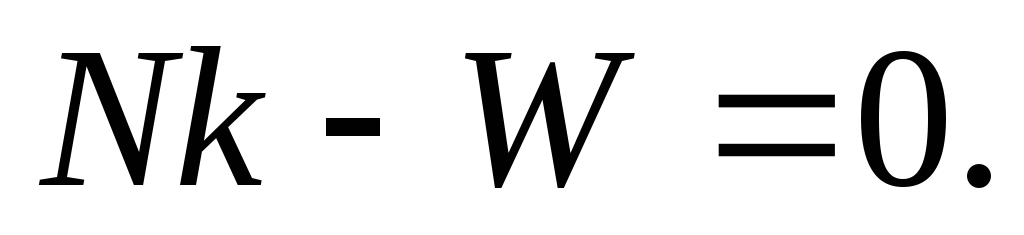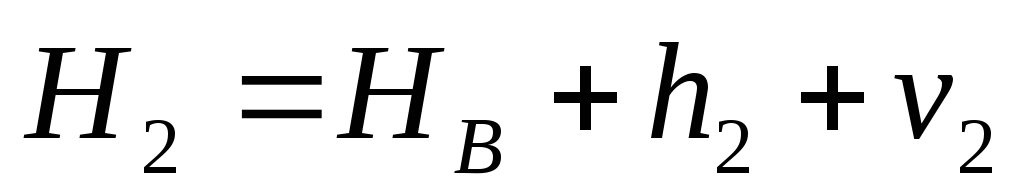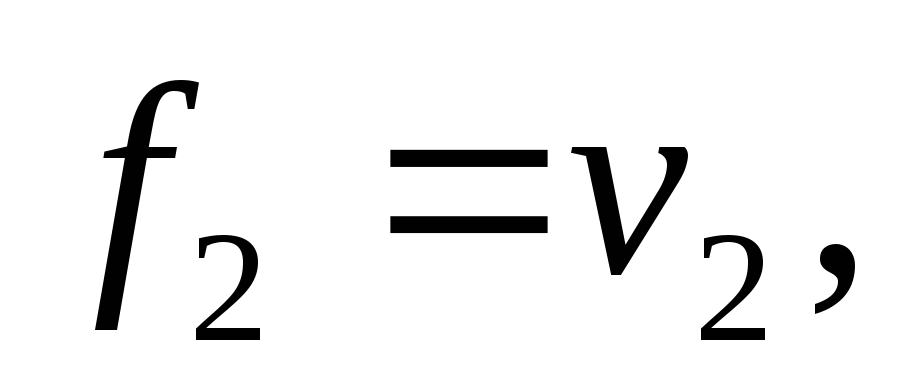Уравнивание нивелирной сети коррелатным способом
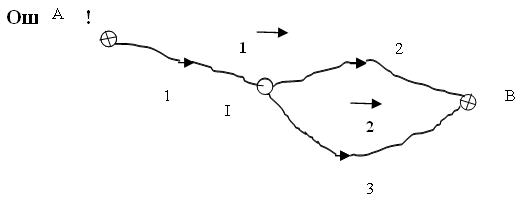
Исходные данные для нивелирной сети, представленной на рис. 1:
НА = 100,000 м; НВ = 110,000 м — отметки исходных пунктов.
h (м): 5,005; 5,015; 5,001 — измеренные превышения.
S (км) : 2; 2; 1 — длины ходов.
pi = c/Si: 0,5; 0,5; 1,0 — веса измерений, с = 1 — постоянная .
Рис. 1. Нивелирная сеть
Определим число независимых условных уравнений.
Уравнивание нивелирной сети начинают с подсчета числа независимых условных уравнений по формуле r = n — t. В сети, представленной на рис. 1, число измеренных превышений n = 3. Число необходимых измерений t = 1 — количеству вновь определяемых пунктов. Таким образом, r = 2.
Составим условные уравнения связи.
В нивелирной сети имеют место полигонные условия: разность суммы превышений в полигоне после уравнивания и теоретической суммы превышений должна быть равна нулю. Выбирают независимые полигоны — замкнутые или разомкнутые, опирающиеся на твердые пункты, в количестве r. На схеме сети показывают номера выбранных полигонов и стрелкой направление суммирования превышений в полигоне. Если направление хода и напрaвление суммирования превышений в полигоне совпадает, знак у превышения «плюс», если не совпадает, превышение следует взять со знаком «минус».
Условные уравнения связи можно записать в форме (4):
Система имеет вид:
(21)
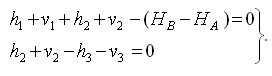
Составим условные уравнения поправок:
Система (21) линейного вида. Для перехода к условным уравнениям поправок достаточно вычислить невязки, которые следует выразить в сантиметрах или миллиметрах, чтобы порядок коэффициентов и невязок был одинаков.
Условные уравнения поправок имеют вид:
(22)
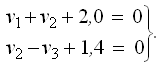
Составим весовую функцию:
В качестве весовой функции целесообразно взять отметку определяемой точки и записать ее математическое выражение через измеряемые превышения от ближайшего исходного пункта.
(23)
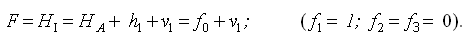
Составим нормальные уравнения коррелат:
Коэффициенты условных уравнений поправок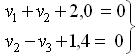 
и весовой функции F = HI = f0 + ν1 поместим по столбцам (табл. 1) в табл. 3. πi = 1/pi — обратный вес результата измерения.
Коэффициенты условных уравнений и функции
Решим в схеме Гаусса (табл. 4) полученную систему нормальных уравнений коррелат, обратный вес функции вычислим в дополнительном столбце схемы ( табл. 2).
Решение нормальных уравнений коррелат
ляемых при решении нормальных уравнений, зависит от тоСледует иметь в виду, что количество запасных знаков, оставчности невязок w и соответствует представленному в данном примере.
Вычислим поправки к результатам измерений:
Поправки вычисляют в табл. 3, вначале piνi, как сумму произведений по строке коэффициентов условных уравнений на соответствующие коррелаты, затем νi:
После этого делают контроль поправок: [pν²]= -[кw] и по формуле (16) в схеме решения нормальных уравнений.
Вычислим уравненные значения измеренных величин:
Вычислим отметку определяемого пункта:
Выполним оценку точности по материалам уравнивания.
— средняя квадратическая ошибка единицы веса (превышения по ходу в 1 км).
— средняя квадратическая ошибка функции.
Дата добавления: 2016-06-24 ; просмотров: 2029 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
З а д а н и е 3. Уравнивание нивелирной сети коррелатным способом
Задание. Уравнять нивелирную сеть, изображенную на рис.1, коррелатным способом. Исходные данные используются по тому же варианту что и при уравнивании сети параметрическим способом.
3.1. Краткая суть коррелатного способа.
Пусть известны истинные значения Х1, Х2, …Хnизмеряемых величин х1, х2, …,х, которые удовлетворяют следующим условиям или условным уравнениям
Если вместо истинных значений принять измеренные, то условия нарушатся и будут иметь вид
Где Wi – свободный член условного уравненияi.
Для их выполнения в измеренные величины х необходимо ввести поправки v . Тогда условные уравнения будут иметь вид
.
Пусть имеется система условных уравнений, записанная в общем виде
где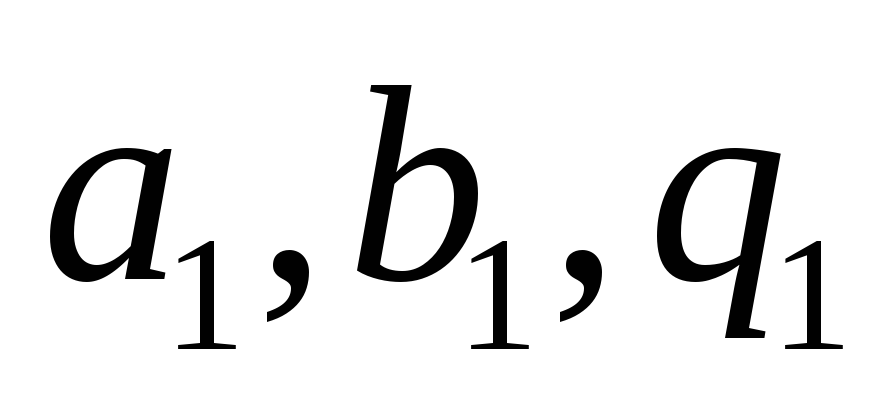 
– коэффициенты условных уравнений (i=1,2,…,r),Wi– их свободные члены (i=1,2,…,r), (2),…,(n) – поправки в измерения.
то матричный вид системы условных уравнений будет
где В – матрица коэффициентов уравнений, а V,W– вектор поправок и свободных членов условных уравнений.
Число условных уравнений в нивелирных ходах
где n– число нивелирных ходов между всеми пунктами,m– число определяемых пунктов.
Алгоритм уравнивания коррелатным способом.
1. Составляется система условных уравнений . Соответственно матрица коэффициентов В и вектор свободных членов W.
2. Вычисляется матрица нормальных уравнений
и решается система нормальных уравнений
3. Находятся поправки к измеренным величинам по формуле
4. Оценка дисперсии любой функции уравненных величин производится по формуле
а оценка стандарта единицы веса вычисляется по формуле
где r– число условных уравнений.
Решение нормальных уравнений обычно ведется по схеме Гаусса.
3. 2. Решение задачи
В сети имеется 6 измерений и 3 определяемых пункта. По этой причине возникает r=6-3=3 условных уравнения, для 3-х полигонов. Полигоны можно сформировать различным образом. При этом 2 полигона обязательно разомкнутыми, а один или замкнутым или разомкнутым. В данном случае сформированы 2 разомкнутых полигона и один замкнутый.
В нивелирных сетях возникают условные уравнения вида
где hi– измеренное превышение, (hi) – поправка в превышение, аHk, Нн– отметки исходных реперов: конечного и начального.
Это уравнение можно записать в виде
где 
В замкнутых построениях Нk=Hн.
Условные уравнения для наших полигонов будут:
При этом невязки в полигонах можно посчитать по формуле
В рассматриваемом примере невязки составят
Оценим также высоты наших станций 1, 2, 3. Для этого составим весовые (оценочные) функции координат точек.
Поскольку координаты исходных пунктов безошибочны, то оценочные функции fбудут следующими
Запишем, как и в параметрическом способе, условные уравнения в табл.19. Также в эту таблицу запишем и оценочные функции. В качестве обратных весов (1/р) примем длины наших ходов в км.
Таблица.19 Система условных уравнений
Система нормальных уравнений получается как и в параметрическом способе, только вместо веса используется обратный вес (1/р). Результат вычисления системы нормальных уравнений записывают в табл.20 следующего вида
Таблица20 Система нормальных уравнений
Полученную систему нормальных уравнений решают по схеме Гаусса, как и в параметрическом способе. Отличие данной схемы от параметрического способа состоит в том, что здесь еще выполняется оценка точности и ищется ковариационная матрица оцениваемых функций. Так при оценке функции f1значение 0,926 было получено по формуле:
Аналогичным образом находятся и остальные элементы ковариационной матрицы.
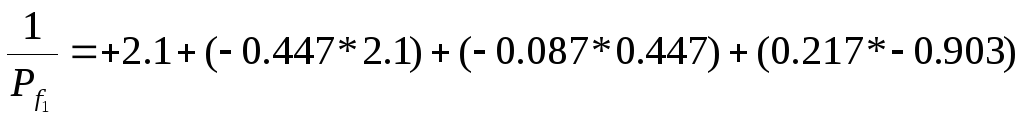
После решения системы нормальных уравнений коррелаты были подставлены в условные уравнения и по формуле поправки в измерения
Поправки в измерения, полученные коррелатным способом, должны совпадать с полученными параметрическим в пределах ошибки округления – 0,1-0,3 мм. Это является контролем правильности вычислений.
Далее вычисляем высоты узловых точек:
Расхождение составило 1 мм, что свидетельствует о наличии только ошибок округления последних двух превышений. При сравнении высот точек полученных коррелатным и параметрическим способом необходимо отметить, что оба способа приводят к одинаковым результатам. Наличие расхождений объясняется лишь ошибками округления.
Для оценки точности высот наших точек определить [pv 2 ] и найти среднюю квадратическую ошибку единицы веса
Таблица решение системы нормальных уравнений по схеме Гаусса с оценкой точности
Источник
