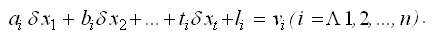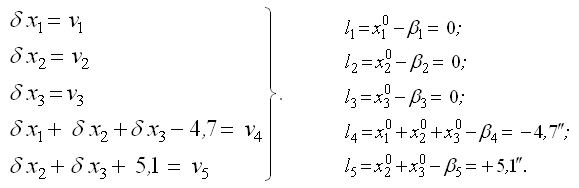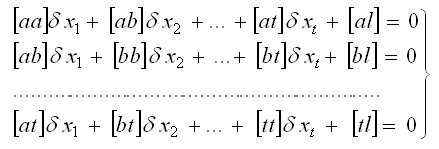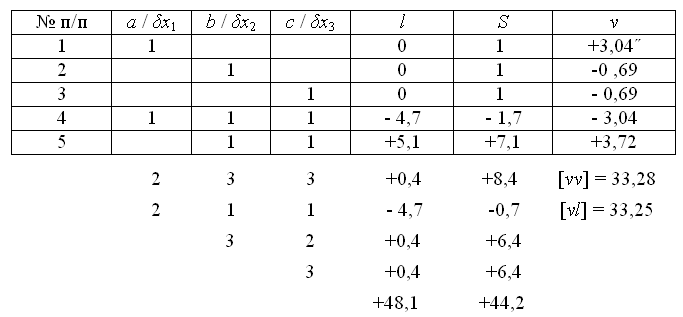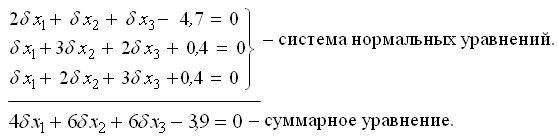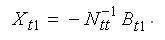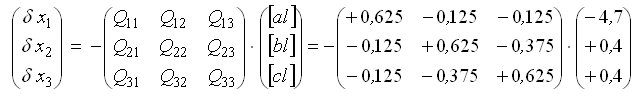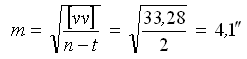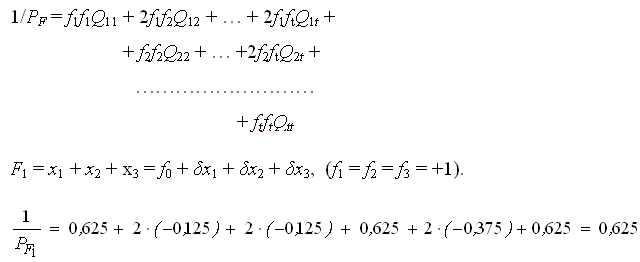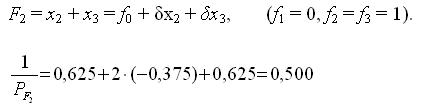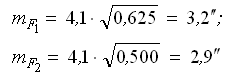Уравнивание углов на станции параметрическим способом
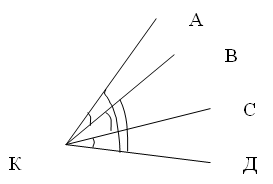
В табл. 13 даны результаты равноточных измерений углов на станции (рис. 4).
Рис. 4. Углы на станции
Результаты измерений βi
| № углов | Углы | βi | № углов | Углы | βi |
| АКВ | 20° 00′ 05,2″ | АКД | 65° 20′20,0″ | ||
| ВКС | 20° 00′ 10,1″ | ВКД | 45° 20′ 05,0″ | ||
| СКД | 25° 20′ 00,0″ |
Число всех измеренных углов n = 5; число необходимых измерений t = 3.
Выберем в качестве параметров х1, х2, х3 соответственно первый, второй, третий углы. Четвертый и пятый углы можно представить как суммы параметров.
Составим параметрические уравнения связи по формуле:
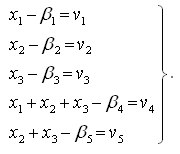
Введем приближенные значения параметров, приняв их равными измеренным значениям соответствующих углов:
Перейдем к параметрическим уравнениям поправок:
Составим нормальные уравнения:
Bычислим коэффициенты и свободные члены нормальных уравнений (табл. 14).
Таблица параметрических уравнений
Систему нормальных уравнений решим методом обращения
Элементы обратной матрицы Ntt -1 получим на ПК, используя математические функции электронных таблиц Еxсel или системы Mathсad.
Контроль вычисления неизвестных:
4·3,038 +6·(-0,688) + 6·(-0,688) — 3,9 = 0.
В табл. 14 по формуле (28) вычислим поправки к результатам измерений. Сделаем контроль решения по МНК.
Найдем уравненные значения углов 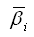
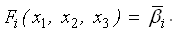
Оценим точность результатов измерений.
— средняя квадратическая ошибка результатов измерений.
Уравненные значения углов. Контроль уравнивания
| № п/п | 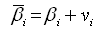 | Параметры и их функции | Fi(x1, x2, x3) |
| 20°00′ 08,24″ | x1 | 20° 00′ 08,24″ | |
| 20° 00′ 09,41″ | x2 | 20° 00′ 09,41″ | |
| 25° 19′ 59,31″ | x3 | 25° 19′ 59,31″ | |
| 65° 20′ 16,96″ | x1 + x2 +x3 | 65° 20′ 16,96″ | |
| 45° 20′ 08,72″ | x2 + x3 | 45° 20′ 08,72″ |
Оценим точность уравненных углов. Обратный вес функции найдем через элементы обратной матрицы по формуле:
— обратный вес первой функции.
— обратный вес второй функции.
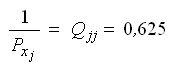
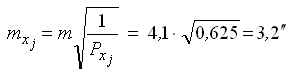
— средние квадратические ошибки весовых функций.
Источник
3. Уравнивание геодезической сети параметрическим способом
3.1. Краткие сведения из алгоритма способа
Сущность параметрического способа отражается в принципах, положенных в основу составления уравнений поправок. Дальнейшая задача сводится к их решению при условии метода наименьших квадратов.
Для составления уравнений поправок выбирают независимые параметры 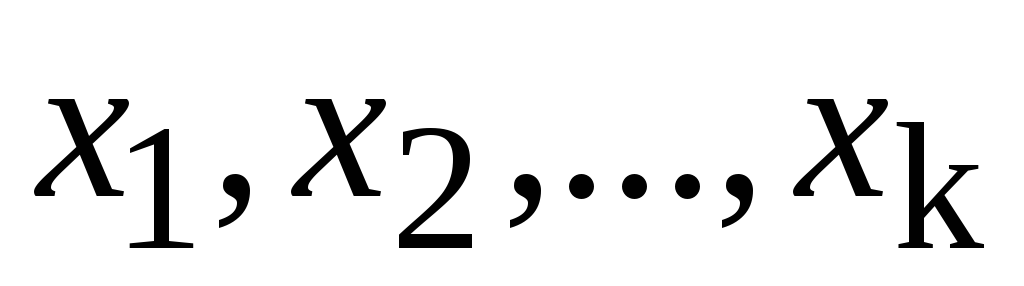
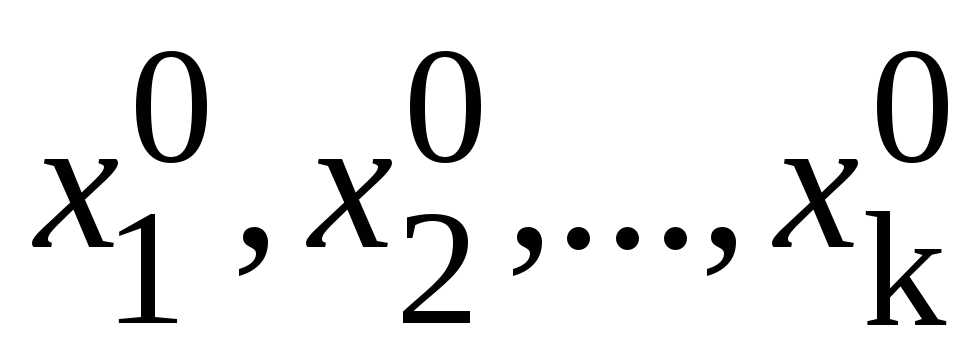
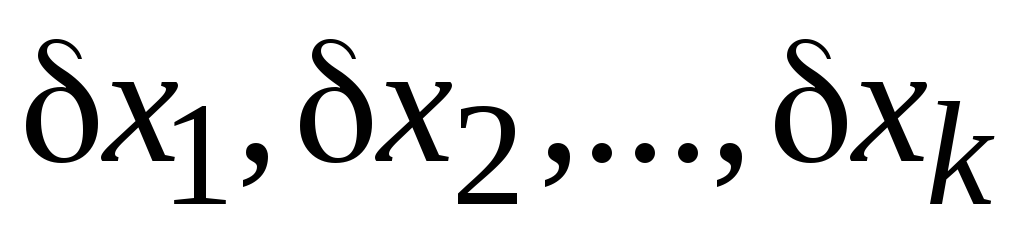
Обозначим численные значения измеренных величин за 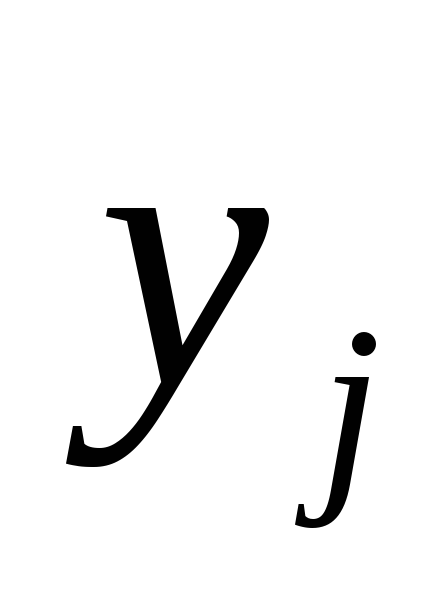
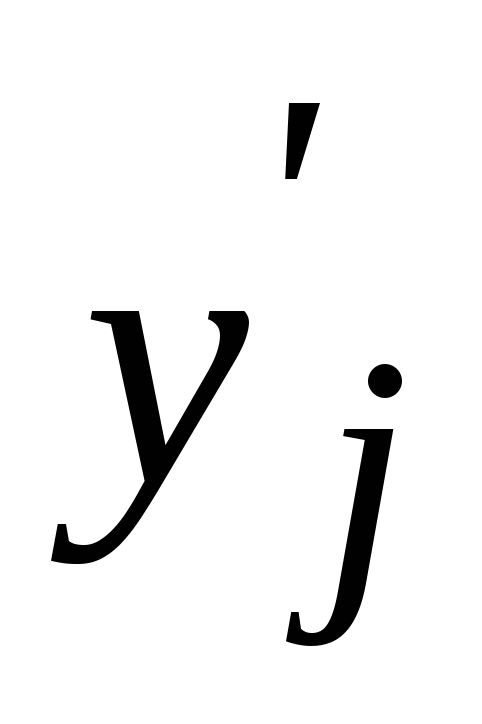
Независимые параметры связаны функциональными зависимостями с уравниваемыми величинами
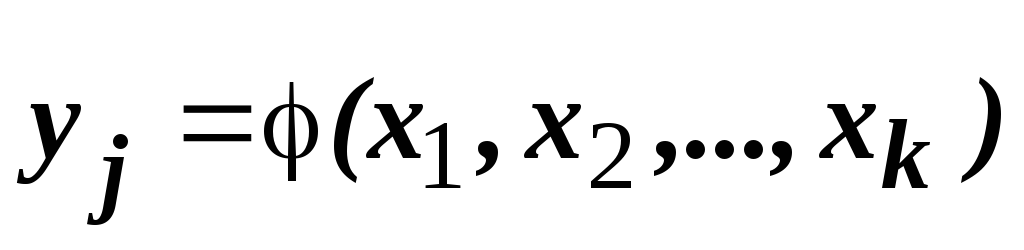
Это выражение называется уравнением связи, оно справедливо и по отношению к уравненным величинам и уравненным параметрам
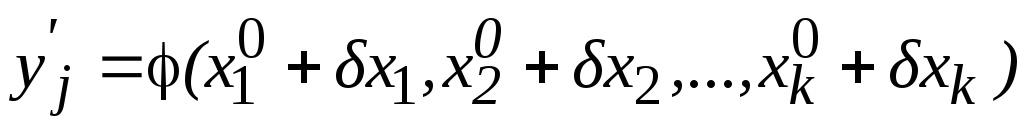
причем 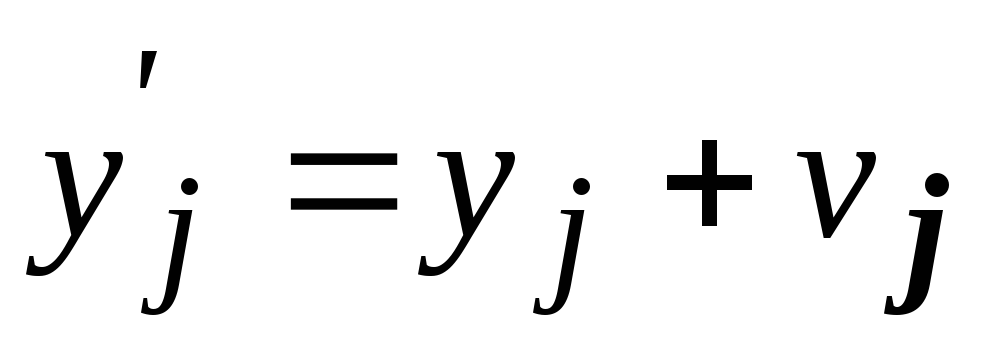


Систему уравнений (19) приводят к линейному виду и получают систему линейных уравнений поправок:

или 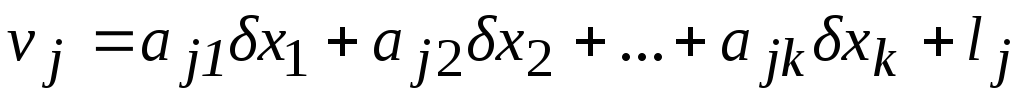
где 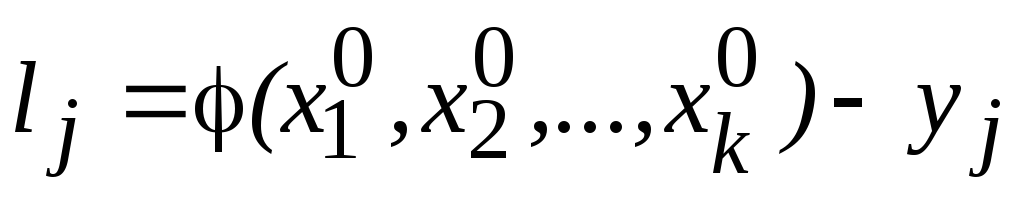

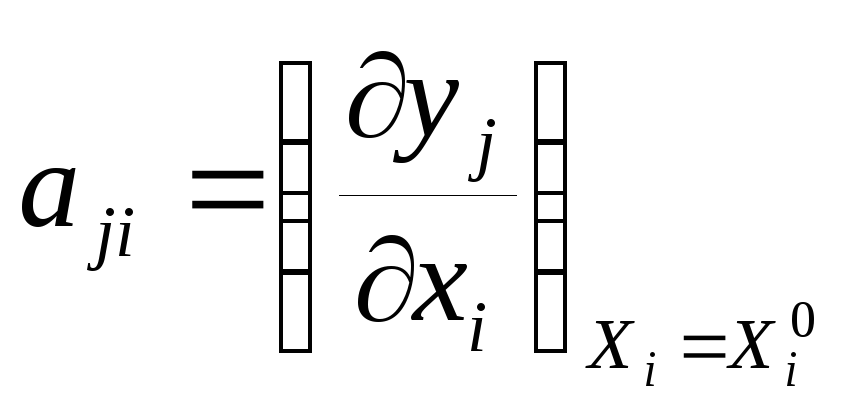
В матричной форме записи система параметрических уравнений имеет вид:
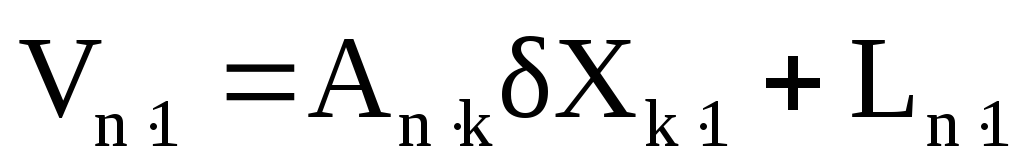
где 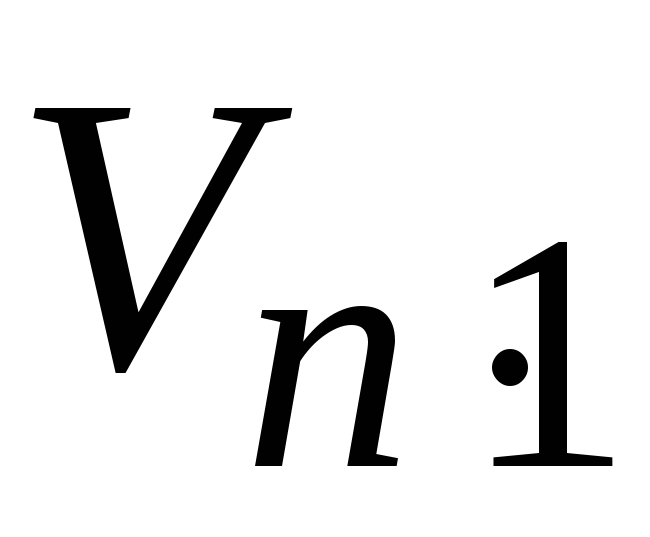
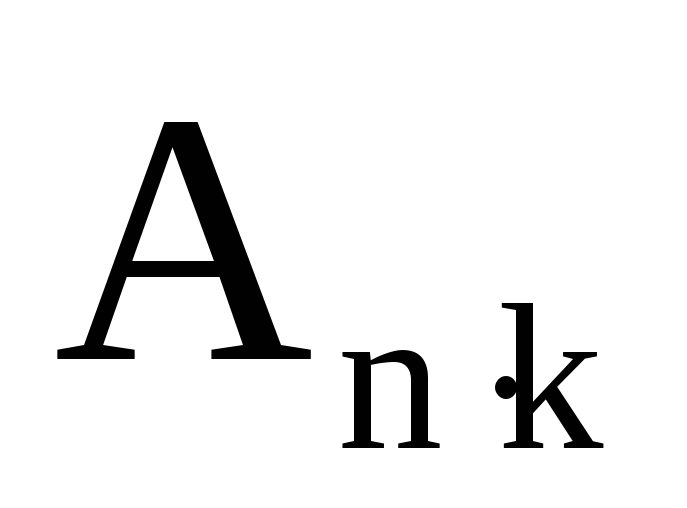
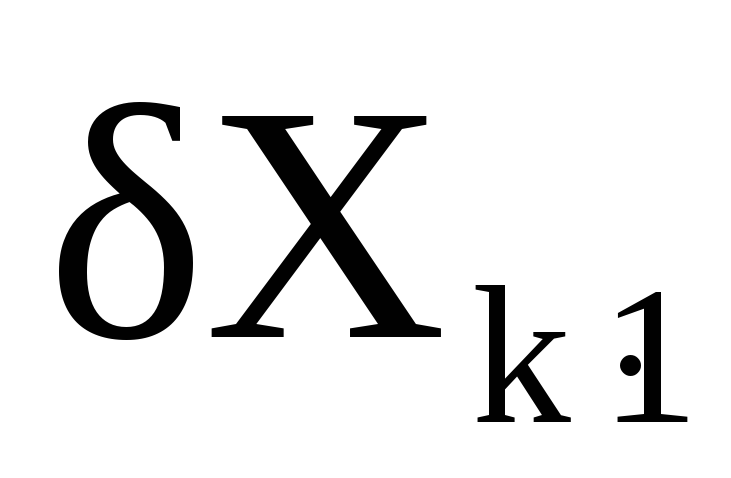

Для приведения системы уравнений к равноточному виду и переходу к системе нормальных уравнений умножим систему (22) слева на 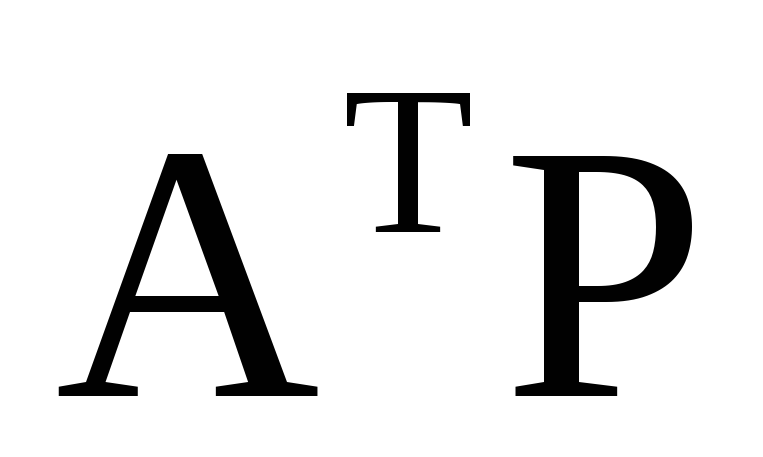

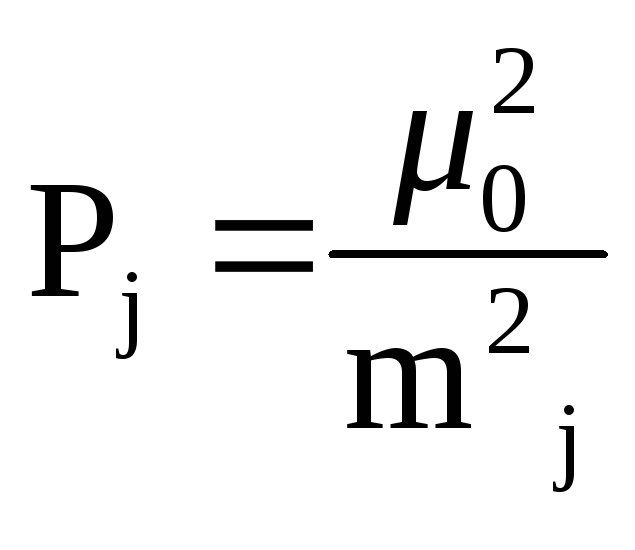
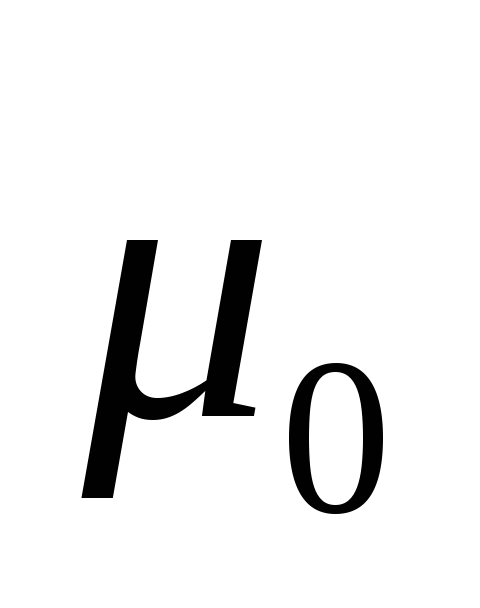
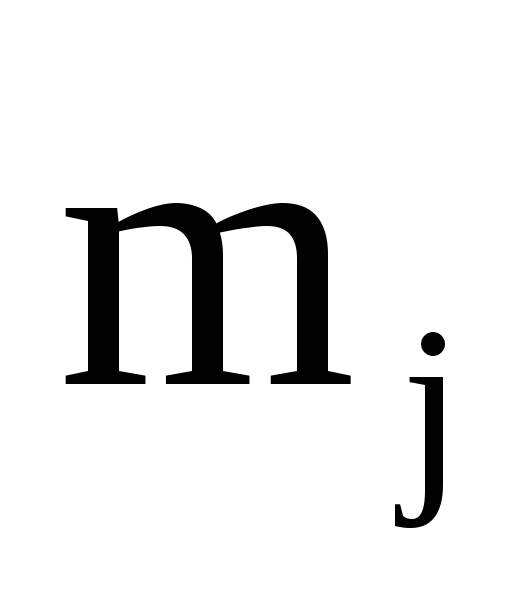
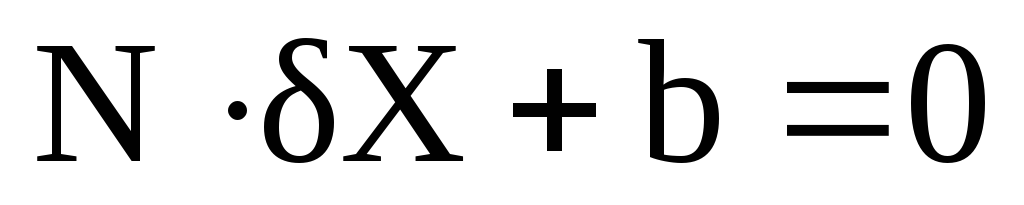
где 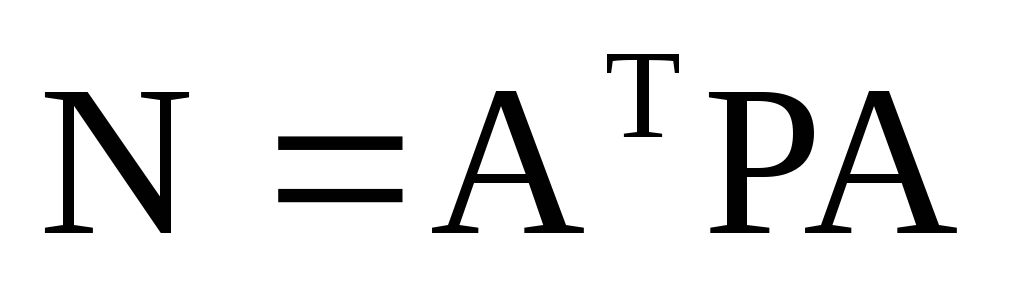
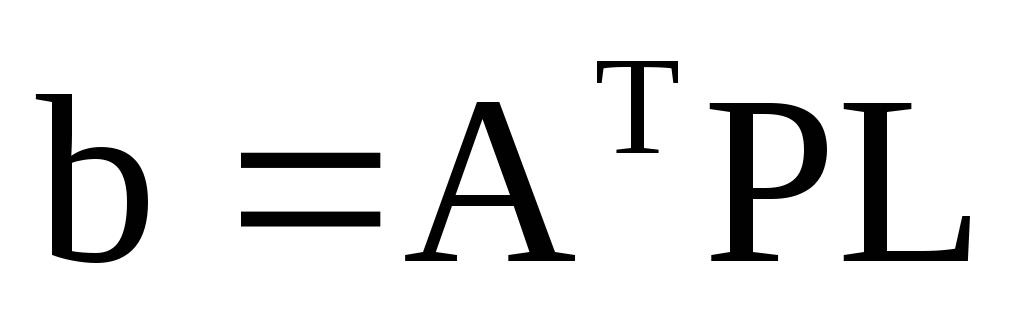
Решение системы (23) находим в виде

где 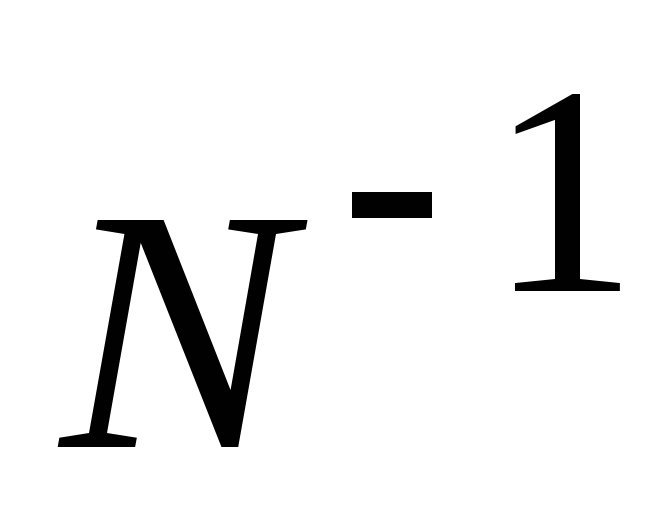
Подставив решение системы нормальных уравнений в выражение (22), найдем вектор поправок в измеренные величины.
После этого необходимо произвести оценку точности. Вычисляют ошибку единицы веса после уравнивания по формуле :
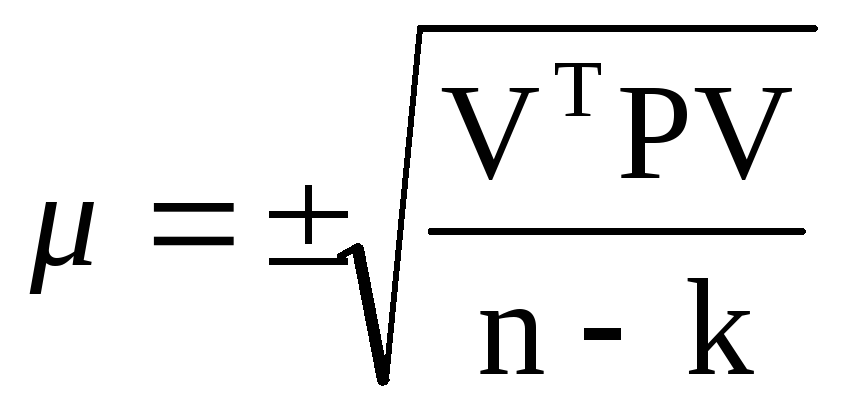
где n –число всех измерений,
k – число параметров;
V T – транспонированный вектор поправок в измеренные величины;
Р – матрица весов измеренных величин;
V — вектор поправок в измеренные величины.
Точность определения параметров из уравнивания характеризуется величиной средней квадратической ошибки, значение которой определяется из соотношения 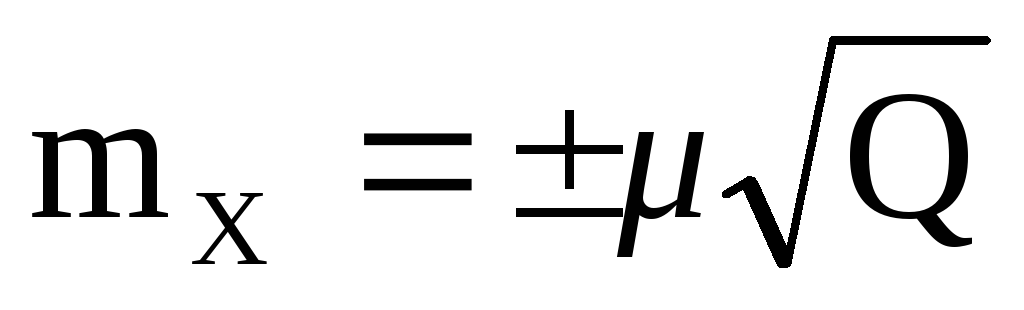
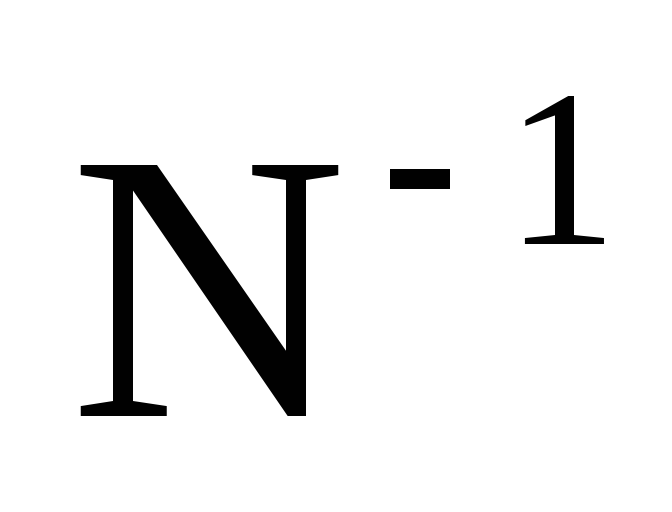
Источник
3. Уравнивание геодезической сети параметрическим способом
3.1. Краткие сведения из алгоритма способа
Сущность параметрического способа отражается в принципах, положенных в основу составления уравнений поправок. Дальнейшая задача сводится к их решению при условии метода наименьших квадратов.
Для составления уравнений поправок выбирают независимые параметры 

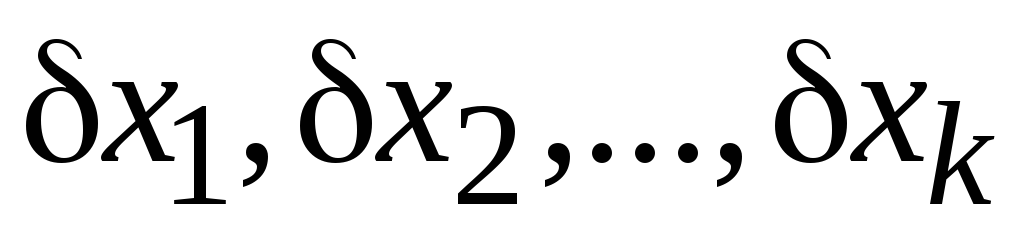
Обозначим численные значения измеренных величин за 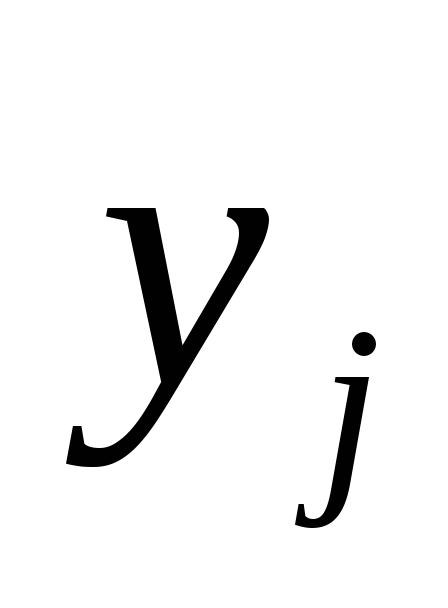

Независимые параметры связаны функциональными зависимостями с уравниваемыми величинами
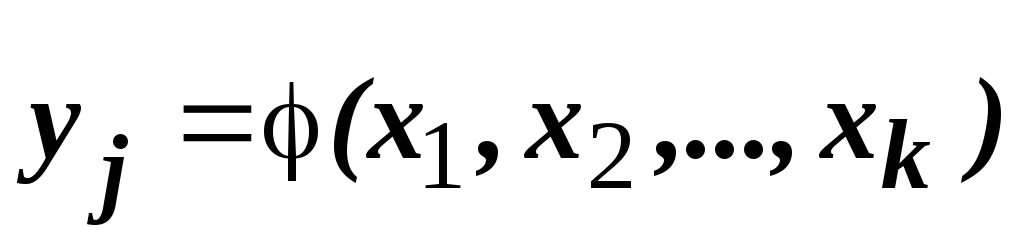
Это выражение называется уравнением связи, оно справедливо и по отношению к уравненным величинам и уравненным параметрам

причем 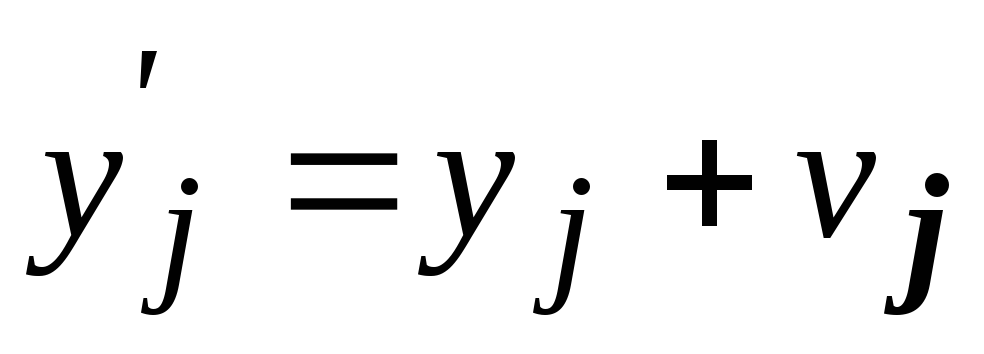



Систему уравнений (19) приводят к линейному виду и получают систему линейных уравнений поправок:
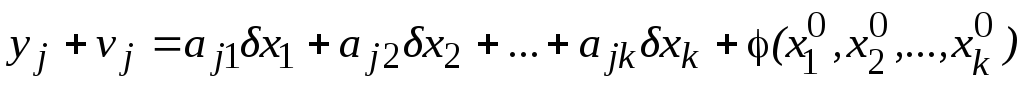
или 
где 


В матричной форме записи система параметрических уравнений имеет вид:
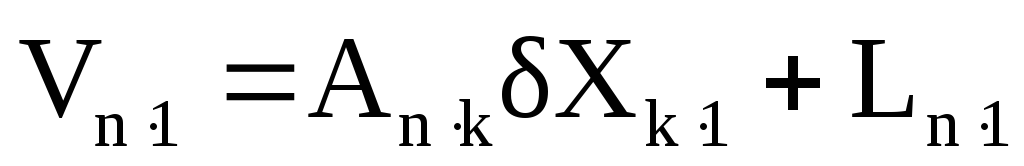
где 



Для приведения системы уравнений к равноточному виду и переходу к системе нормальных уравнений умножим систему (22) слева на 



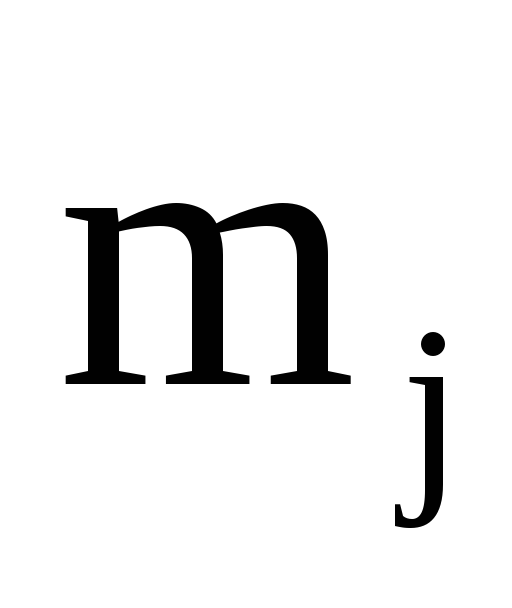

где 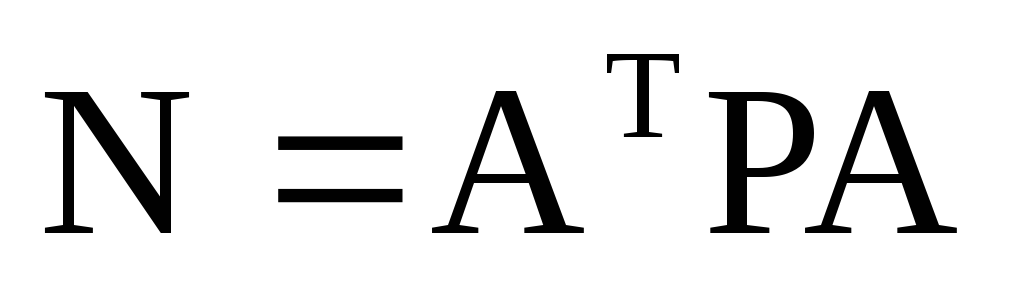

Решение системы (23) находим в виде
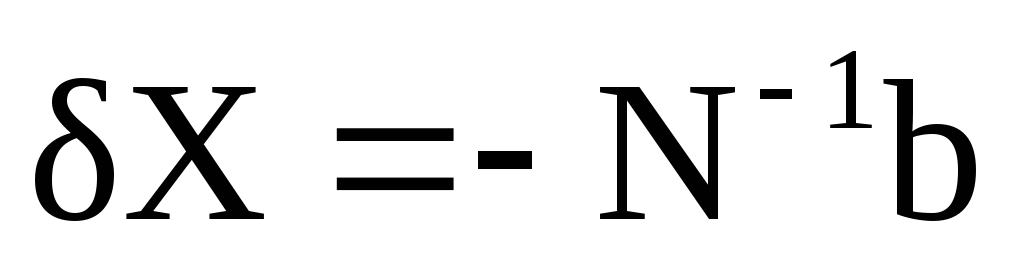
где 
Подставив решение системы нормальных уравнений в выражение (22), найдем вектор поправок в измеренные величины.
После этого необходимо произвести оценку точности. Вычисляют ошибку единицы веса после уравнивания по формуле :

где n –число всех измерений,
k – число параметров;
V T – транспонированный вектор поправок в измеренные величины;
Р – матрица весов измеренных величин;
V — вектор поправок в измеренные величины.
Точность определения параметров из уравнивания характеризуется величиной средней квадратической ошибки, значение которой определяется из соотношения 
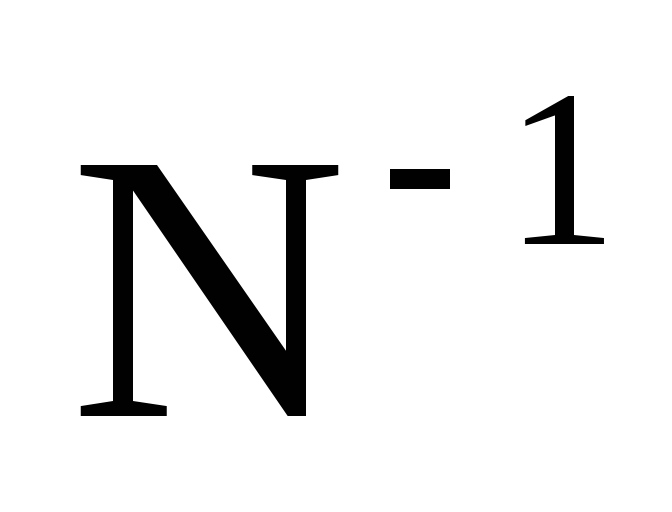
Источник