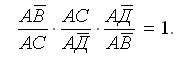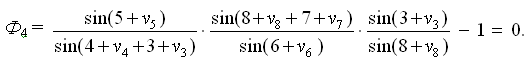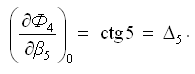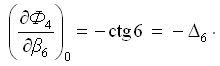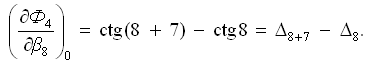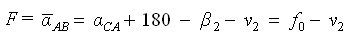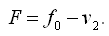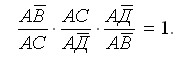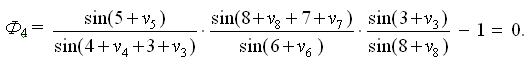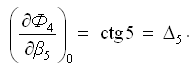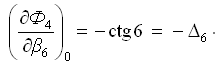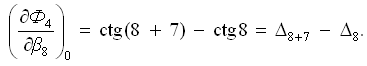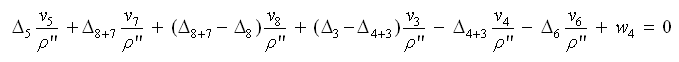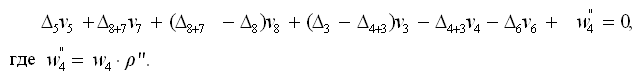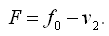Уравнивание геодезического четырехугольника коррелатным способом
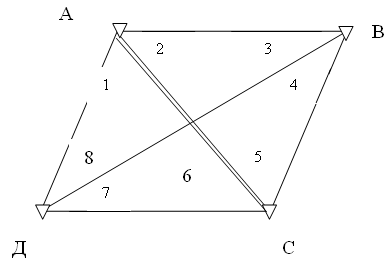
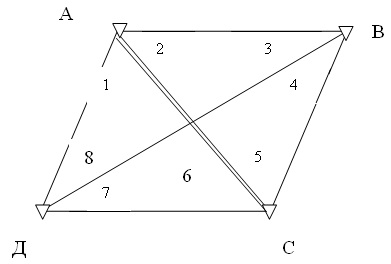
Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n — t = 8 — 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
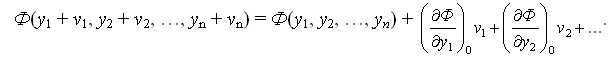
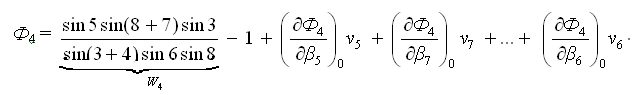
Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
| . | Числитель | . | . | Знаменатель | . |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
Полюсное условное уравнение поправок принимает вид:
Составим весовую функцию.
— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
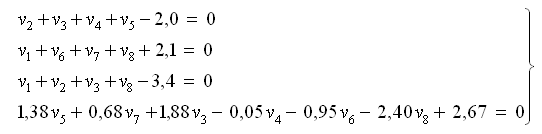
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| . | ||||||
| -1 | . | |||||
| +1.88 | . | |||||
| -0.05 | . | |||||
| +1.38 | . | |||||
| -0.95 | . | |||||
| +0.68 | . | |||||
| -2.40 | . |
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения — m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции — mF.
Вычислите уравненные значения углов 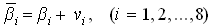
Дата добавления: 2016-06-24 ; просмотров: 3588 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Уравнивание геодезического четырехугольника коррелатным способом
Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
Рис. 2. Геодезический четырехугольник
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n — t = 8 — 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 — условных уравнения фигур и 1 — полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс — точка А, то
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
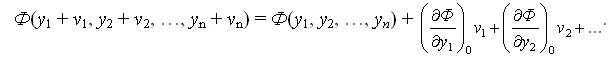
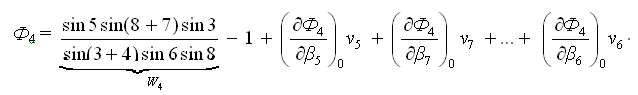
Частная производная функции Ф4 по аргументу β5 (углу числителя):
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
Умножив на ρ″, получим
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
| . | Числитель | . | . | Знаменатель | . |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
Полюсное условное уравнение поправок принимает вид:
Составим весовую функцию.
— дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
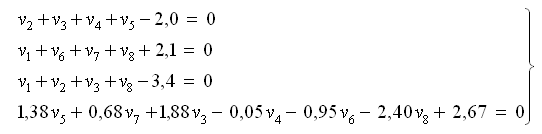
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| . | ||||||
| -1 | . | |||||
| +1.88 | . | |||||
| -0.05 | . | |||||
| +1.38 | . | |||||
| -0.95 | . | |||||
| +0.68 | . | |||||
| -2.40 | . |
и весовая функция:
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения — m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции — mF.
Вычислите уравненные значения углов 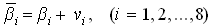
Дата добавления: 2014-09-08 ; просмотров: 1068 ; Нарушение авторских прав
Источник
РЕШЕНИЕ ГЕОДЕЗИЧЕСКОГО ЧЕТЫРЕХУГОЛЬНИКА



1.1. Исходные данные
Плановое обоснование для разбивки на местности опор мостового перехода выполнено методом геодезического четырехугольника, схема которого представлена на рис. 1. Опорные точки 5, 6, 11 и 12 закреплены на местности по типу временных геодезических знаков в виде столиков для установки теодолита. На каждой точке измерены углы электронным теодолитом 3Та5р, значения которых указаны на рис. 1. Среднеквадратическая погрешность измерения одного угла (паспортная точность теодолита) составляет m = ± 5″. На этом же рис.1 в кружках обозначены номера углов № 1,2,3,4,5,6,7,8, в квадратиках номера треугольников № 1, 2, 3, и стороны буквами A,B,C,D,E,F. Для определения допуска на угловую погрешность устанавливается коэффициент значимости t = 1,96 ≈ 2,0, который ограничивает величину фактической погрешности измерений в 95%.
Дирекционный угол линии 5-6 (α56), длина линии A (d56) и координаты опорной точки 6 (X6, Y6). принимаются каждым студентом индивидуально по номеру варианта (табл. 1), назначаемому преподавателем.
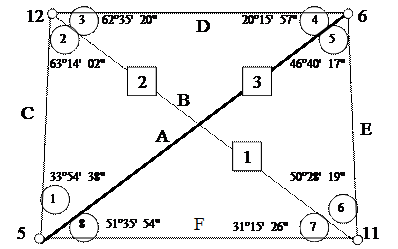 |
Рис. 1 Схема геодезического четырехугольника
1.2. Уравнивание углов, вычисление сторон и координат
Уравнивание углов (табл. 2), вычисление сторон (табл. 3) и координат (табл. 4) геодезического четырехугольника выполнить в стандартных ведомостях.
Уравнивание углов. В соответствии с исходными данными (см. рис. 1) в ведомость уравнивания углов (см. табл. 2, колонка 2) выписать углы измеренные. При этом использовать нумерацию углов рис. 1 и соответствующую нумерацию углов в табл. 2 (колонка 1).
Вычислить сумму восьми измеренных углов ( 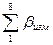
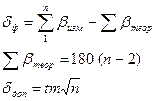
где n – количество измеренных углов;
t – коэффициент значимости (см. выше “исходные данные”);
m – паспортная точность теодолита, используемого для измерения углов, (см. выше “исходные данные”).
Вычислить суммы углов (см. рис. 1)
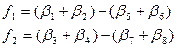
По данным вычисления невязок f1 и f2 выполнить оценку точности измерения углов, используя формулы (1). Если каждая невязка f1 и f2 меньше или равна соответствующей допустимой невязке, то продолжить вычисления.
Вычислить поправки в углы по формулам:
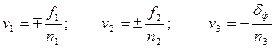
Причем, поправки v1 в углы β1, β2 принять со знаком минус, в углы β5, β6 – со знаком плюс, и поправки v2 в углы β3, β4 – со знаком плюс, в углы β7, β8 – со знаком минус. Поправки v3 во все углы принять со знаком противоположным знаку невязки δф.
| № угла | Углы измеренные, β ° ‘ « | Суммы (1+2) (5+6) (3+4) (7+8) | Невязки f1= β(1+2) — β(5+6) f2= β(3+4) — β(7+8) | Поправки | Углы уравновншенные β ° ‘ « | № угла |
| По условиям β(1+2) = β(5+6) β(3+4) = β(7+8). ± f1/4 ± f2/4 | По условию ∑β(1-8) = ∑βт —δ/8 | Суммарные поправки, v∑ | ||||
| 33 54 38 | 97 08 40 | f1 =97 08 40 — 97 08 36 = + 0 00 04 | -1,0 | +0,875 | -0,125 | 33 54 37,9 |
| 63 14 02 | -1,0 | +0,875 | -0,125 | 63 14 01,9 | ||
| 46 40 17 | 97 08 36 | +1,0 | +0,875 | +1,875 | 46 40 18,9 | |
| 50 28 19 | +1,0 | +0,875 | +1,875 | 50 28 20,9 | ||
f1(доп)=±mt 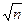 =±2*2 =±2*2 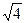 = ±8″ = ±8″ | ∑ 0,0 | ∑ +3,500 | β(1+2) = 97 08 39,8 β(5+6) = 97 08 39,8 | |||
| 62 35 20 | 82 51 17 | f2 =82 51 17 -82 51 20 = — 0 00 03 | +0,75 | +0,875 | +1,625 | 62 35 21,6 |
| 20 15 57 | +0,75 | +0,875 | +1,625 | 20 15 58,6 | ||
| 31 15 26 | 82 51 20 | -0,75 | +0,875 | +0,125 | 31 15 26,1 | |
| 51 35 54 | -0,75 | +0,875 | +0,125 | 51 35 54,1 | ||
f2(доп)=±mt 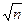 =±2*2 =±2*2 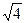 = ±8″ = ±8″ | ∑ 0,00 | ∑ +7,000 | ∑ +3,500 | β(3+4) = 83 51 20,2 β(7+8) = 83 51 20,2 | ||
| ∑β(1-8) | 359 59 53 | ∑ +7,000 | ∑β(1-8)=360 00 00 | |||
δф = ∑β(1-8) — ∑βт δф =359 59 53–360 00 00 = — 0 00 07 δдоп = ± m t 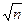 = ±2*2 = ±2*2 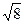 = ± 11,3″ = ± 11,3″ |
Вычисление сторон (решение треугольников)
| № треу-голь-ника | № точки | № угла | Уравновешенные углы, β ° ‘ « | Sin углов Sin β | Вычисленная длина сторон, d, м | Поправки в длины сторон, м | Исправлен-ная длина сторон, d, м | Обозначение сторон |
| 6+7 | 81 43 47,0 | 0,98960054 | 492,480 | 492,480 | А | |||
| 51 35 54,1 | 0,78367569 | 390,000 | 0,000 | 390,000 | E | |||
| 46 40 18,9 | 0,72743652 | 362,013 | 0,000 | 362,013 | F | |||
| 180 00 00,0 | ||||||||
| 2+3 | 125 49 23,5 | 0,81082695 | 492,480 | 0,000 | 492,480 | A | ||
| 20 15 58,6 | 0,34638358 | 210,386 | 0,000 | 210,386 | C | |||
| 33 54 37,9 | 0,55789761 | 338,856 | +0,001 | 338,857 | D | |||
| 180 00 00,0 | ||||||||
| 50 28 20,9 | 0,77131889 | 338,856 | +0,001 | 338,857 | D | |||
| 4+5 | 66 56 17,5 | 0,92008283 | 404,211 | +0,001 | 404,212 | B | ||
| 62 35 21,6 | 0,88772970 | 389,998 | +0,002 | 390,000 | E | |||
| 180 00 00,0 |

vE = — fd = +0.002; vD = vB = 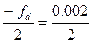
Ведомость вычисления координат точек опорной сети
| № то-чек | Углы исправ-ленные ° ‘ « | Дирек-ционные углы ° ‘ « | Исправ-ленные стороны d, м | Вычисленные прирашения координат, м | Поправки, м | Исправленные приращения координат, м | Координаты, м | № то-чек |
| ∆X | ∆Y | δX | δY | ∆X | ∆Y | X | Y | |
| прав | ||||||||
| 21 55 18,0 | ||||||||
| 46 40 18,9 | 2954,980 | 5068,740 | ||||||
| 155 14 59,1 | 390,000 | -354,175 | 163,279 | -354,175 | 163,279 | |||
| 50 28 20,9 | 2600,805 | 5232,019 | ||||||
| 284 46 38,2 | 404,212 | 103,099 | -390,842 | +0,001 | 103,100 | -390,842 | ||
| 296 45 58,1 | 2703,905 | 4841,177 | ||||||
| 168 00 40,1 | 210,386 | -205,797 | 43,702 | -205,797 | 43,702 | |||
| 326 05 22,1 | 2498,108 | 4884,879 | ||||||
| 21 55 18,0 | 492,480 | 456,871 | 183,862 | +0,001 | -0,001 | 456,872 | 183,861 | |
| 2954,980 | 5068,740 | |||||||
| ∑β | 720 00 00,0 | ∑d =1497,078 | ∑∆X= -0,002 | ∑∆Y= + 0,001 | ∑ δX= + 0,002 | ∑δY= -0,001 | ∑∆X = 0,000 | ∑∆Y= 0,000 |
| ∑βт | 720 00 00,0 | fx = — 0.002 | fy = +0.001 | |||||
| f(абс) = ± 0.002 | ||||||||
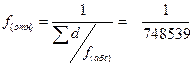 | f(отн, доп) = 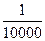 |
Все вычисленные поправки округлить точностью до 0,1″. Учитывая знаки соответствующих поправок вычислить суммарные поправки для каждого угла v∑ = v1 + v3; v∑ = v2 + v3.
Исправить измеренные углы βиспр = βизм + v∑, при этом необходимо учитывать знаки суммарных поправок. Вычисления выполнить с точностью 0,1″.
Выполнить контрольные вычисления сумм поправок и сумм углов. Данные уравновешивания углов и контрольных вычислений записать в табл. 2 в соответствующие колонки и строки (см. табл. 2).
Вычисление сторон (решение треугольников). По номерам указанным в квадратиках (см. рис. 1) определить номера треугольников и нумерацию их вершин. В соответствии с номером треугольника установить последовательность их записи в ведомость вычисления сторон (см. табл. 3). Для каждого треугольника в ведомости вычисления сторон (см. табл. 3) установить последовательность нумерации точек, которая должна начинаться с номера угла напротив известной стороны А (см. рис. 1), затем продолжаться номером угла напротив промежуточной стороны и заканчиваться номером угла напротив связующей стороны (стороны принадлежащей двум последовательным треугольникам). Из ведомости уравнивания углов (см. табл. 2) в ведомость вычисления сторон (см. табл. 3) в третью колонку выписать уравновешенные углы. Причем необходимо выписать углы в соответствии с их нумерацией указанной в колонке 2 табл. 3. В случае указанной суммы углов произвести их суммирование. Для каждого треугольника (см. рис. 1) вычислить контрольные суммы углов, которые должны быть точно равны 180°. Установить синусы всех углов треугольников с точностью до 0,000000001.
В соответствии с вариантом решения задачи (см. табл. 1) в ведомость вычисления сторон (см. табл. 3) в соответствующие строки и колонки выписать численное значение исходной стороны A (см. рис.1). В ведомости вычисления сторон (см. табл. 3) последовательно, начиная с первого треугольника, вычислить промежуточные и связующие стороны по формуле:
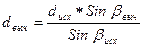
где dвыч – вычисляемая сторона треугольника;
dисх – исходная (известная) сторона треугольника (для первого и второго треугольника сторона А, см. рис. 1 и табл. 3);
Sinβвыч – синус угла треугольника, находящегося напротив вычисляемой стороны (см. табл. 3);
Sinβисх – синус угла треугольника, находящегося напротив известной стороны (см. табл. 3).
Вычисления по формуле (4) сторон (см. рис. 1) E и F в первом треугольнике и сторон C и D во втором треугольнике выполнить по известной исходной стороне А (см. рис. 1 и табл. 3). Вычисление сторон B и E в третьем треугольнике выполнить по стороне D, значение которой установлено из вычислений во втором треугольнике. Сопоставить численные значения стороны E установленные по вычислениям в первом (E1) и третьем (E3) треугольнике. Принять за вероятнейшее значение стороны Е, численное ее значение (E1), полученное из первого треугольника. В этом случае невязку установить по формуле:
Вычислить поправки для сторон E и B третьего треугольника и для стороны D третьего и второго треугольников по формулам (см. табл. 3):
vE = — fd; и vB = vD = 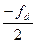
Вычислить исправленные стороны по формуле:
Данные вычислений записать в соответствующие графы и колонки табл. 3.
Вычисление координат. Исходными данными для вычисления координат точек опорной сети в стандартной ведомости (см. табл. 4) являются уравновешенные углы (см. табл. 2), исходный дирекционный угол (α56), принимаемый в соответствии с вариантом решения задачи (см. табл. 1), вычисленными длинами сторон (см. табл. 3) и координатами исходной точки 6, принимаемыми в соответствии с вариантом решения задачи (см. табл. 1).
В первую очередь необходимо принять последовательность нумерации точек. Для этого можно использовать следующие варианты (см. рис.1):
В качестве примера решения задачи в настоящих методических указаниях принят вариант по последовательности (8) (см. табл. 4).
Из ведомости уравнивания углов (см. табл. 2) в ведомость вычисления координат (см. табл. 4) выписать левые по принятому варианту последовательности нумерации точек уравновешенные углы. Углы будут левыми, если мысленно встать на предыдущую точку, например 5, и повернувшись лицом по направлению последующей точки (точки 6) на этой последующей точке угол будет слева по ходу. В противном случае углы будут правыми. Например, для последовательности (8) углы будут левые, а для последовательности (9) – правые.
Проверить правильность выписки углов путем их суммирования. При этом, поскольку на двух (m = 2) точках 11 и 5 необходимо вычислять левые по ходу углы, как дополнения до 360°, то теоретическая сумма углов будет равна:
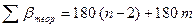
По принятому варианту решения задачи из табл. 1 в ведомость вычисления координат выписать исходный дирекционный угол (α56), который записать в соответствующие строки колонки 3 (см. табл. 4).
Вычислить дирекционные углы остальных линий хода по формуле:
для левых углов, принятых по последовательности точек (8)
или для правых углов, если принята последовательность точек (9)
Если при вычислении по формуле (11) αпред + βлев 360°, то αпосл = αпред + βлев — 180° — 360°.
Если при вычислении по формуле (12) αпред + 180° 360°, то αпосл = αпред + 180° — βправ — 360°.
Контролем правильности вычисления дирекционных углов служит критерий точного равенства вычисленного дирекционного угла α56, при последовательном вычислении по формулам (11) или (12) и того же угла, записанного как исходного для линии 5-6 в нижней строке третьей колонки табл. 4.
Из ведомости вычисления сторон (см. табл. 3.) в ведомость вычисления координат (см. табл. 4, колонка 4) по принятой последовательности вычислений (8) или (9) выписать соответствующие стороны. Вычислить приращения координат по формулам:
Подсчитать в соответствующих колонках табл.4
и вычислить невязки по осям координат:
Вычислить абсолютную погрешность:
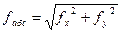
и, наконец, относительную погрешность, которая должна удовлетворять неравенству
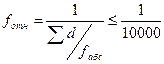
В случае выполнения неравенства (18) можно продолжить вычисления. В противном случае проверить правильность выписки сторон из ведомости их вычисления или правильность вычислений по формулам (13), (14) или вычисления сумм ∑di; ∑∆Xi; ∑∆Yi, а также вычисления по формулам (15), (16), (17) и (18).
Определить поправки в приращения координат vx и vy с точностью 0,001 метра. При этом необходимо использовать следующие принципы: знаки поправок должны быть обратными по отношению к знаку невязок, вычисленных по формулам (15), (16); большие численные значения поправок vx и vy должны соответствовать большим численным значениям сторон (d) полигона; сумма поправок ∑vx или ∑vy должна быть равна с обратным знаком соответствующим невязкам fx или fy. Если быть точным, то поправки необходимо вычислять по формулам:
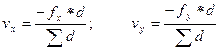
при точном выполнении условий
Однако вычисления по формулам (19) небольших численных значений невязок приводят к поправкам, которые могут иметь значащую цифру только в четвертом или пятом разряде после запятой. Такие поправки для практической цели не имеют смысла. Поэтому необходимо выдержать требование округления поправок с точностью 0,001 метра и выше сформулированные принципы. Это достигается путем введения поправок равных 0,001 м в приращения координат только для тех сторон, которые имеют большие численные значения. Для других приращений координат поправки будут равны нулю. В любом случае при определении поправок должны выполняться условия (20).
Вычислить исправленные приращения координат:
Вычислить координаты точек опорной сети:
Контролем вычисления координат опорной сети является следующее правило: координаты последней точки (исходной), вычисленные при использовании формул (23) или (24), должны быть точно равны координатам той же исходной точки.
Источник