Виды уравнений и методы их решения

В разработке рассматриваются виды алгебраических уравнений и методы их решения.
Просмотр содержимого документа
«Виды уравнений и методы их решения»
Виды уравнений и методы их решения
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Рассмотрим более подробно их виды и алгоритм решения.
Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня.
Дробные и иррациональные уравнения можно свести к решению целых уравнений.
Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями первой степени, квадратные — второй, а кубические, соответственно, третьей.
Рассмотрим особенности решения алгебраических уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Остановимся на основных понятиях.
Тождество — это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком 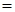
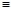
Уравнение — это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:a, b, c. – или теми же буквами, снабженными индексами: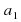
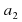
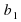
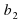
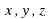
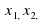
В общем виде уравнение может быть записано так:
F (
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Рассмотрим некоторые эквивалентные уравнения:
Уравнение 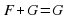
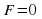
Уравнение 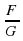
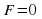
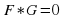
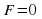
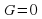
Уравнение 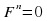
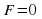
Уравнение 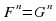
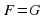
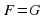
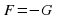
Алгебраическим уравнением называется уравнение вида 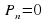
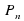
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида:
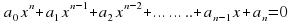
где n – неотрицательное целое число; коэффициенты многочлена называются , ……коэффициентами (или параметрами), называется неизвестным и является искомым. Число n называется степенью уравнения.
Значения неизвестного , обращающие алгебраическое уравнение в тождество, называются корнями (решениями) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида , где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
Главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка (и) пересечения двух графиков даст решение (я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
Рассмотрим методы решения уравнений.
Линейным уравнением называется уравнение первой степени.
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень , который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число -b, получаем уравнение
, (2) эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину , получаем корень уравнения (1):
Алгебраическое уравнение второй степени (3),
где a, b, с– некоторые действительные числа, называется квадратным уравнением.
Если , то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
Выражение называется дискриминантом квадратного уравнения.
если , то уравнение имеет два различных действительных корня;
если , то уравнение имеет один действительный корень кратности 2;
если , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если ), которое обычно записывается в виде
Корни приведенного квадратного уравнения вычисляются по формуле
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
Корни этого квадратного уравнения удобно вычислять по формуле
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения
связаны с его коэффициентами Формулами Виета
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если , , то оба корня отрицательны;
если , , то оба корня положительны;
если , , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если , , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
то корни квадратного уравнения вычисляются по формуле
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
Заметим, что , поэтому
но , из формулы (7) поэтому окончательно
Если положить, что + , то
Заметим, что , поэтому
но , поэтому окончательно
Уравнения n-й степени вида
называется двучленным уравнением. При и заменой (2))
где — арифметическое значение корня, уравнение (8) приводится к уравнению
которое и будет далее рассматриваться.
Двучленное уравнение при нечетном n имеет один действительный корень . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и комплексных):
Двучленное уравнение при четном n в множестве действительных чисел имеет два корня , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение при четном n имеет один действительный корней , а в множестве комплексных чисел корней, вычисляемых по формуле
Двучленное уравнение при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
Уравнение имеет два действительных корня .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение имеет два действительных корния и два комплексных корня .
Уравнение действительных корней не имеет. Комплексные корни: .
Уравнение имеет один дествительный корень и два комплексных корня
Уравнение действительных корней не имеет. Комплексные корни:
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
оказались «крепким орешком». В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
разделить на , то коэффициент при станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:
Чтобы не путаться в коэффициентах, заменим здесь на и перегруппируем слагаемые:
Мы видим, что надлежащим выбором , а именно взяв , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
Если здесь сделать замену , получим кубическое уравнение относительно без члена с :
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу :
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
и взять в качестве сумму и . Заменой , эта система приводится к совсем простому виду:
Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при со знаком минус, а произведение – свободному члену. Отсюда следует, что и — корни уравнения
Выпишем эти корни:
Переменные и равны кубическим корням из и , а искомое решение кубического уравнения (13) – сумма этих корней:
Эта формула известная как формула Кардано.
подстановкой приводится к «неполному» виду
Корни , , «неполного» кубичного уравнения (14) равны
Пусть «неполное» кубичное уравнение (14) действительно.
а) Если («неприводимый» случай), то и
Во всех случаях берется действительное значение кубичного корня.
Алгебраическое уравнение четвертой степени.
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой уравнение сводится к квадратному уравнению с последующим решением двух двучленных уравнений и ( и — корни соответствующего квадратного уравнения).
Если и , то биквадратное уравнение имеет четыре действительных корня:
Если , (3)), то биквадратное уравнение имеет два действительных корня и мнимых сопряженных корня:
Если и , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени
можно избавиться от члена подстановкой . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
Идея Феррари состояла в том, чтобы представить уравнение в виде , где левая часть – квадрат выражения , а правая часть – квадрат линейного уравнения от , коэффициенты которого зависят от . После этого останется решить два квадратных уравнения: и . Конечно, такое представление возможно только при специальном выборе параметра . Удобно взять в виде , тогда уравнение перепишется так:
Правая часть этого уравнения – квадратный трехчлен от . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
Это уравнение называется резольвентным (т.е. «разрешающим»). Относительно оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень . При правая часть уравнения (15) принимает вид
а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде
и добавим к обеим частям выражение , чтобы в левой части образовался полный квадрат:
Теперь приравняем к нулю дискриминант правой части уравнения:
или, после упрощения,
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: . После подстановки этого значения получим уравнение
откуда . Корни образовавшихся квадратных уравнений — и . Разумеется, в общем случае могут получиться и комплексные корни.
подстановкой приводится к «неполному» виду
Корни , , , «неполного» уравнения четвертой степени (16) равны одному из выражений
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие
причем , и — корни кубичного уравнения
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени ( ) можно «обслужить» одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени при неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его «Мемуаре об условиях разрешимости уравнений в радикалах» (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь является корнем многочлена с целыми коэффициентами, то ее числитель является делителем свободного члена , а знаменатель — делителем старшего коэффициента .
Для доказательства достаточно подставить в уравнение и умножить уравнение на . Получим
Все слагаемые в левой части, кроме последнего, делятся на , поэтому и делится на , а поскольку и — взаимно простые числа, является делителем . Доказательство для аналогично.
С помощью этой теоремы можно найти все рациональные корни уравнения с целыми коэффициентами испытанием конечного числа «кандидатов». Например, для уравнения
старший коэффициент которого равен 1, «кандидатами» будут делители числа –2. Их всего четыре: 1, -1, 2 и –2. Проверка показывает, что корнем является только одно из этих чисел: .
Если один корень найден, можно понизить степень уравнения. Согласно теореме Безу,
остаток от деления многочлена на двучлен равен , т. е. .
Из теоремы непосредственно следует, что
Если — корень многочлена , то многочлен делится на , т. е. , где — многочлен степени, на 1 меньшей, чем .
Продолжая наш пример, вынесем из многочлена
множитель . Чтобы найти частное , можно выполнить деление «уголком»:
Источник




