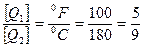Уравнение шкалы физической величины способы задания шкал

Шкалы физических величин.

Величины оценивают при помощи шкал. Шкала величины — упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений.

Шкала физической величины — это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений. Термины и определения теории шкал измерений изложены в документе МИ 2365-96.

В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.

1. Шкалы наименований (шкалы классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности. Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.

Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.

2. Шкалы порядка (шкалы рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить, во сколько раз больше или меньше конкретные проявления свойства.

Условная шкала — это шкала порядка ФВ, исходные значения которой выражены в условных единицах. Например, шкала вязкости Энглера, 12-балльная шкала Бофорта для измерения силы морского ветра.

Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк — 1; гипс — 2; кальций — 3; флюорит — 4; апатит —■ 5; ортоклаз — 6; кварц — 7; топаз — 8; корунд — 9; алмаз — 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем G) на нем остается след, а после ортоклаза F) — не остается, то твердость Испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно.

Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным.

3. Шкалы интервалов (шкалы разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало — нулевую точку. К таким шкалам относится летосчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо Рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий бессмысленно.

Шкала интервалов величины Q можно представить в виде Q =Q₀ + q[Q], где q — числовое значение величины; Q₀ — начало отсчета шкалы; [Q] — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Q₀ шкалы и единицы данной величины [Q]. Задать шкалу можно двумя путями. При первом пути выбираются два значения Q₀ и Q_l величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q₁ — Q₀) — основным интервалом. Точка Q₀ принимается за начало отсчета, а величина (Q₁ — Q₀)/n = [Q] за единицу Q. При этом число единиц n выбирается таким, чтобы [Q] было целой величиной. Перевод одной шкалы интервалов Q = Q_0l + q_l[Q]_l в другую Q=Q₀₂ + q₂[Q]₂ осуществляется по формуле

(1.1)

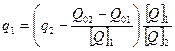
При втором пути единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирается каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1 с = 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

4. Шкалы отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы первого рода — аддитивные), а в ряде случаев и пропорциональности (шкалы второго рода — пропорциональные). Их примерами являются шкалы массы (второго рода) и термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений. С формальной точки зрения шкала отношений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении ФВ. Шкалы отношений — самые совершенные. Они описываются уравнением Q=q[Q], где Q — ФВ, для которой строится шкала; [Q] — ее единица измерения; q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q₂ = q_l [Q₁]/ [Q₂].

5. Абсолютные шкалы. Под абсолютными понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Пример.

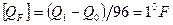
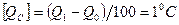
Шкала Фаренгейта является шкалой интервалов. На ней Q₀ — температура смеси льда, поваренной соли и нашатыря, Q₁ — температура человеческого тела. Единица измерения — градус Фаренгейта: . Температура таяния смеси льда, соли и нашатыря оказалась равной 32°F, а температура кипения воды — 212°F. По шкале Цельсия Q₀ — температура таяния льда, Q₁ — температура кипения воды. Градус Цельсия .

Требуется получить формулу для перехода от одной шкалы к другой.

Решение. Формула для перехода определяется в соответствии с выражением (1.1). Значение разности температур по шкале Фаренгейта между точкой кипения воды и точкой таяния льда составляет 212°F — 32°F = 180°F. По шкале Цельсия интервал температур равен 100°С. Следовательно, 100°С = 180°F и отношение размеров единиц

Числовое значение интервала между началами отсчета по рассматриваемым шкалам, измеренного в градусах Фаренгейта ([Q]_l = F), равно 32. Переход от температуры по шкале Фаренгейта к температуре по шкале Цельсия производится по формуле

Источник

Шкалы измерений. Основное уравнение измерений

Основное уравнение измерений

Для установления различия в количественном содержании ото­бражаемого данной физической величиной свойства изучаемых объектов (явлений, процессов) введено понятие «размер физической величины» – количественная оп­ределенность физической величины, присущая конкретному мате­риальному объекту, системе, явлению или процессу. Истинный размер физи­ческой величины является объективной реальностью, не завися­щей от того, измеряют соответствующую характеристику свойст­ва объекта или нет.

Ко­личественной оценкой физической величины является значение физической величины– выражение размера физической величины в виде некоторого числа принятых для нее единиц.

Числовое значение физической величины – отвлеченное число, входящее в значение величины.

Данные определения формализовано выражаются в виде:

где Х – физическая величина;

q – числовое значение величины Х;

[Х] – единица измерения величины Х.

Например, за единицу измерения напряжения электрического тока принят 1 В. Тогда значение напряжения электрической сети U = q [U] = 220 [1B] = 220B. Здесь числовое значение q = 220. Но если за единицу напряжения принять [1 кВ], то U = q [U] = 0,22 [1 кВ] = 0,22 кВ, т. е. числовое значение q = 0,22, а размер величины не изменяется.

Уравнение (2.1) называется основным уравнением измерений, показывающим, что числовое значение величины зависит от размера принятой единицы измерения.

Упорядоченная совокупность значений физической величины, служащая исходной основой для измерений данной величины, называется шкалой физической величины.

Все виды шкал измерений разделяются на следующие:

1) шкалы наименований характеризуются только отношением эквивалентности различных качественных проявлений свойства. Эти шкалы не имеют нуля и единицы измерений, в них отсутствуют отношения сопоставления типа «больше – меньше». Пример шкал наименований: шкалы цветов, представляемые в виде атласов цве­тов;

2) шкалы порядка свойства величин описывают как отношением эквивалентности, так и отношением порядка по возрастанию или убыванию количественного проявления свойства. В этих шкалах может в ряде случаев иметься нуль (нулевая отметка), но прин­ципиальным для них является отсутствие единицы измерения, по­скольку невозможно установить, в какое число раз больше или меньше проявляется свойство величины. Примеры шкал порядка: шкалы чисел твердости, баллов силы ветра, землетрясений;

3) шкалы интервалов (разностей) описывают свойства величин не только с помощью отношений эквивалентности и порядка, но также и с применением суммирования и пропорциональности ин­тервалов (разностей) между количественными проявлениями свойства. Шкалы разностей могут иметь условные нули и единицы измерений, установленные по согласованию. Так, по шкале интервалов времени их можно суммировать (вычитать) и сравни­вать, во сколько раз один интервал больше (меньше) другого;

4) шкалы отношений описывают свойства величин, для множеств количественных проявлений которых применимы логические отно­шения эквивалентности, порядка и пропорциональности, а для некоторых шкал также отношение суммирования. В шкалах отношений существует естественный нуль и по согласованию устанавливается единица измерения. Примерами шкалы отношений яв­ляются шкалы массы и термодинамической температуры;

5) абсолютные шкалы, кроме всех признаков шкал отношений, обладают дополнительным признаком: в них естественно, одно­значно присутствует определение единицы измерения. Абсолют­ные шкалы присущи относительным единицам таким, как коэф­фициенты усиления, ослабления, полезного действия и др. Ряду абсолютных шкал, например, коэффициентов полезного действия присущи границы, заключенные между нулем и едини­цей.

Шкалы наименований и порядка относятся к условным (неметрическим) шкалам – шкала физической величины, исходные значения которой выражены в условных единицах. Шкалы интервалов, отношений и абсолютные называются метрическими.

Источник

Метрология, стандартизация и сертификация

Лекция 1. Метрология

1. Метрология и ее значение в научно-техническом прогрессе.

2. Физические величины и единицы их измерений. Физические величины. Понятие о системе физических величин.

3.Принципы построения Международной системы единиц.

4. Преимущества Международной системы единиц

1. Метрология и ее значение в научно-техническом прогрессе

Измерения являются одним из важнейших путей познания природы, дают количественную характеристику окружающего нас мира, помогают раскрыть действующие в природе закономерности. Они дают возможность обеспечить взаимозаменяемость узлов и деталей, совершенствовать технологию, безопасность труда и других видов человеческой деятельности, улучшать качество продукции.

Круг величин, подлежащих измерению, определяется разнообразием явлений, с которыми приходится сталкиваться человеку. Сравнение опытным путем измеряемой величины с другой, подобной ей и принятой за единицу, составляет общую основу любых измерений.

Метрология — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

В метрологии решаются следующие основные задачи:

• разработка общей теории измерений физических величин и их систем;
• разработка методов и средств измерений;
• разработка методов определения точности измерения;
• разработка основ обеспечения единства и единообразия средств измерений;
• разработка эталонов и образцовых средств измерений;
• разработка методов передачи размеров единиц от эталонов и образцовых средств измерений к рабочим средствам измерений.

Источник