Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4. Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4.1 Общие указания и исходные данные
Простой и в то же время строгий способ уравнивания ходов технического нивелирования способом полигонов предложил профессор В.В.Попов. Этот способ сводится к последовательному распределению невязок в каждом полигоне пропорционально длинам ходов. При этом если в соседнем полигоне уже было произведено распределение невязок, то на величину поправки, пришедшейся на общий обоим полигонам ход, нужно предварительно исправить с учётом её знака невязку этого подлежащего увязанию полигона. Таким образом, дело сводится к методу последовательных приближений. Применение способа Попова требует расположения вычислений в определенной схеме. Удобно эти вычисления производить на схеме расположения ходов, как это рекомендует сам автор.
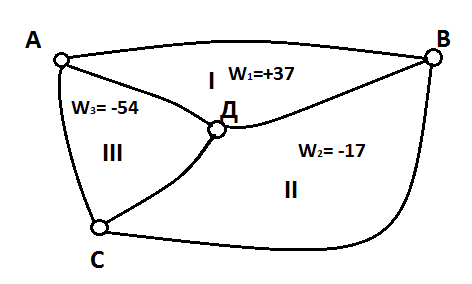
Перед уравниваем я вычертила схему нивелирной сети (приложение Г), на которую выписала по ходам и полигонам периметры, измеренные превышения, фактические и допустимые невязки в сумме превышений по полигонам. Для установления знака невязки направление обхода в каждом полигоне выбрала по ходу часовой стрелки. Контролем правильности вычисления невязок является условие [fh]=0. вычислила допустимые невязки по формуле:
где L – периметр полигона, км.
Предварительно исправила исходные данные, учитывая свой порядковый номер. Эти вычисления производятся в таблице 11. Длину ходов вычислила по формуле: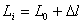 
, (24),
∆l = +0.2км * №=0,16 км. Высота исходных реперов HRp1=106.985 –
4.2 Уравнивание превышений по способу полигонов профессора В.В.Попова
Далее вычертила схему независимых нивелирных полигонов, на которую выписала невязки полигонов (приложение Д). Невязки в превышениях выписаны внутри соответствующих полигонов в прямоугольных рамках. Полигоны пронумерованы.
Рядом с ходами, идущими по периметру полигонов, подготовила таблички для записи значений поправок. Поправки по каждому ходу выбрасывались за полигон, таким образом для внутренних ходов – по две таблички и по одной с каждой внешней стороны.
Для каждого хода вычислила коэффициент пропорциональности или «красные числа» по формуле:
ri=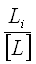 
(25),
где Li – длина хода, [L] – периметр хода. Найденные отношения выписала на схему над табличками поправок для каждого хода красным цветом. Контролем правильности вычисления этих чисел является равенство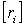 
= 
по каждому полигону (например, для полигона I «красные числа» получились 0.22, 0.25, 0.28, 0.25, в сумме они действительно дают единицу).
Начала распределение невязок с полигона, имеющего наибольшую по абсолютной величине невязку. В моем варианте этим полигоном является полигон II с невязкой -14. Невязки в полигонах распределяют пропорционально «красным числам». Итак, умножала невязку полигона на соответствующие этому полигону «красные числа», округляя до целых, и записывала в таблички, лежащие вне полигона, причем со знаком, одинаковым знаку невязки. Контролем является: сумма поправок должна дать величину невязки.
Перешла к следующему полигону (III). В нем ход 12-13 уже получил поправку, поэтому невязку этого полигона следовало изменить на величину поправки хода 12-13. Полученная остаточная невязка вписывается в рамку под числом исходной невязки полигона III. Далее эту остаточную невязку умножала на соответствующие этому полигону «красные числа». Полученные поправки выписываем в рамки, находящиеся вне этого полигона. Каждый раз производила контроль вычислений!
И так далее, переходила к следующему полигону по часовой стрелке и выполняем те же операции (исправляла исходную невязку полигона с учетом поправок, пришедших из других полигонов, и распределяла поправки пропорционально «красным числам», выполняя контроль). Так, когда вернулась к полигону II, значит завершила первый круг распределения невязок. Перешла ко второму кругу, повторяя все в том же порядке.
В полигоне II невязку я уже распределила, но в этом полигоне имеются поправки, пришедшие из других полигонов. Сложив их, получила новую невязку этого полигона, которую должна распределить вышеописанным порядком, вписывая вторичные поправки по ходам в соответствующие рамки.
Таким же путем прошла по всем другим полигонам во втором круге. После перешла к третьему, четвертому и так далее. В моем случае, потребовалось пройти 5 кругов.
Теперь необходимо в каждой рамке подсчитать алгебраическую сумму поправок. Для внешних ходов нужно у найденных результатов сложения по каждому ходу изменить знак на обратный и перенести внутрь полигона. Так, например, у хода 2-12 поправка равна -19, перенеся ее внутрь II-ого полигона, получим поправку для хода 2-12, равную 19. Для общих ходов каждой пары смежных полигонов имеются по две рамки, расположенные по разные стороны хода. Вычислила поправки по каждому ходу как разность между суммами поправок по внутренней и внешней табличкам. Эти величины вписала при данном ходе, каждую внутри соответствующего полигона.
Контролем служит то, что сумма поправок по всем ходам полигона должна дать взятую с обратным знаком величину первоначальной невязки, приходящуюся на данный ход (в моем случае по каждому полигону получилось, что сумма поправок по всем ходам совпала с первоначальной невязкой, взятой с противоположным знаком:
по I полигону – 12 мм, по II – 14 мм , по III — 8 мм, по IV — 14 мм, по V – 12мм).
Источник
Уравнивание полигонов по способу В.В.Попова. Оценка точности
Способ проф. В.В. Попова применяется для уравнивания как свободной, так и несвободной сети полигонов.
Для нивелирной сети этот способ является строгим, т.е. дает такие же результаты, что и метод наименьших квадратов. Применительно же к сети теодолитных полигонов он не является строгим, поскольку при этом способе производится раздельное уравнивание углов и приращений координат.
Уравнивание нивелирной сети
Рассмотрим сеть, состоящую из трех полигонов. Убедившись в допустимости невязок, переходят к уравниванию сети. Для этой цели строят новый схематический чертеж сети крупных размеров, на котором непосредственно производится вычисление поправок на звенья.На этом чертеже примерно в центре каждого полигона строят рамочки, над которыми римскими цифрами пишут номера полигонов, а внутри рамочек записывают невязки. Затем вне каждого полигона у каждого его звена строят рамочки для записи поправок. Для каждого звена полигона вычисляют красные числа ki, ki,j (i — номер данного полигона, j — номер смежного с ним). Красным числом называется отношение числа станций в звене к числу станций во всем полигоне (или отношение длины звена к периметру полигона).
Сумма красных чисел для каждого полигона должна быть равна единице (например, в первом полигоне 0,46 + 0,23 + + 0,31 = 1).. Затем приступают к распределению невязок пропорционально красным числам соответствующих полигонов. Это распределение невязок производят непосредственно на чертеже сети, применяя при этом метод последовательных приближений.Умножив невязку первого полигона (I) на его красные числа, полученные произведения, сумма которых должна быть равна распределяемой невязке (—25 — 12 — 17 = —54), записывают в соответствующих данному полигону рамочках. Распределенную невязку подчеркивают.Переходят к полигону II. Здесь значение невязки изменится на величину поправки, перешедшей из полигона I (+38 — 12 == = +26). Учтенную поправку подчеркивают. Новую невязку распределяют пропорционально красным числам этого полигона (0,26; 0,46; 0,28) и полученные произведения (+7, +12, +7), сумма которых должна быть равна распределяемой невязке, записывают во внешних к полигону рамочках под соответствующими красными числами. Распределенную невязку подчеркивают.В полигоне III будет новая невязка, равная сумме начальной невязки и поправок, перешедших из полигонов I и II (+36—17 + + 7 = +26). Учтенные поправки подчеркивают. Полученную невязку распределяют таким же путем, как и в первых двух полигонах, и подчеркивают.
Закончив распределение невязок во всех полигонах, возвращаются к полигону I. Здесь появится новая невязка, равная сумме поправок, перешедших из смежных полигонов. Эта невязка распределяется так же, как и первый раз.Таким образом, закончив первый цикл распределения невязок, приступают ко второму, затем к третьему и так далее до тех пор, пока все невязки полигонов станут равными нулю.
Следует помнить, что во избежание повторного использования одной и той же величины в процессе распределения невязок каждое использованное значение необходимо сразу же подчеркнуть.
После того как все невязки будут распределены, подсчитывают суммы чисел во всех табличках у звеньев.
Правильность вычисления этих сумм контролируют по формулам. Расхождение при этом контроле не должно превышать 1,5 единицы последнего знака суммы.
Затем вычисляют поправки на звенья каждого полигона, считая направление звеньев совпадающим с направлением обхода полигона. Иначе говоря, чтобы получить поправки на звенья, внешние суммы полигона переносят внутрь полигона с противоположным знаком и складывают с его внутренними суммами для тех же звеньев, считая внутреннюю сумму равной нулю, если звено является внешним. В каждом полигоне сумма поправок на звенья должна равна невязке полигона с обратным знаком [например, для i полигона I: +14 +18 +22 = +54 = —(—54)].Введя поправки в измеренные превышения, получают исправленные (уравненные) их значения, по которым вычисляют затем отметки узловых точек.
По поправкам на звеньях можно определить среднюю квадратическую погрешность нивелирования хода длиной 1 км по формуле:
где, Li — длина звена, r — число полигонов.Оценка точности будет надежна только в том случае, когда число полигонов r не слишком мало.Если требуется вычислить высоты точек, расположенных внутри какого-либо звена, то производится уравнивание превышений в этом звене по п 
правилу одиночного хода.
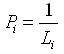
Прямая угловая засечка.
Решаем способом: по дирекционным углам направлений с исходных пунктов на определяемый.(Гаусса)
Прямая геодезическая засечка применяется для определения координат дополнительной точки на основании двух исходных пунктов с известными координатами на местности, неудобной для производства линейных измерений. Для этого достаточно, установив теодолит последовательно на исходных пунктах 1 и 2 , измерить горизонтальные углы b1 и b2 между исходной стороной 1-2 и направлениями на определяемую точку Р.Вычисление координат искомой точки может быть выполнено по формулам Юнга и Гаусса, не требующим предварительного решения треугольника. В этом случае должен соблюдаться определенный порядок нумерации исходных пунктов, отвечающих правилу: если встать в середине линии между исходными пунктами лицом к искомому пункту Р, то исходный пункт. Находящийся слева будет первым, а справа – вторым. Тогда координаты точки Р определятся по формулам котангенсов внутренних углов треугольника (формулам Юнга).
Координаты оп 
ределяемой точки Р могут быть также получены по формулам тангенсов и котангенсов дирекционных углов (формулам Гаусса). Если значение одного из дирекционных углов будет близким к 0 0 или 180 0 , то вычисление координат точки Р удобно производить по формулам тангенсов дирекционных углов: 
. В случае, когда значение одного из дирекционных углов будет близким к 90 0 или 270 0 , вычисление по вышеуказанным формулам становится неудобным вследствие большой величины тангенса этого дирекционного угла. В этом случае выгодно пользоваться формулами котангенсов дирекционных углов.
Билет 18.
1.Задача на веса. 
+ 
+ 
, 
, 
, P= 
( что говорил он 
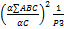
Дата добавления: 2018-04-04 ; просмотров: 1530 ; Мы поможем в написании вашей работы!
Источник
Уравнивание нивелирной сети способом красных чисел ( Попова В.В.)
Схема для уравнивания нивелирных полигонов по способу профессора Попова В.В.
| № варианта | Длины ходов в км | Невязки полигонов, мм | ||||||
| АВ | ВС | СА | АД | ДВ | ДС | W1 | W2 | W3 |
| 21,2 | 18,6 | 9,6 | 9,2 | 6,6 | 21,1 | +37 | -17 | -54 |
На схеме уравнивания нивелирной сети в центре каждого полигона строим рамки, внутри которых записывают невязки( 
, 
, 
) Вне полигона у каждого его звена строим рамки для записи поправок( (I),(II),(III)); у внешних будет по одной рамке, а у внутренних – по две.
Вычисляем красные числа для всех звеньев полигонов
Р1 = АВ + ДВ+ АД = 37
Р2 = ДВ + ВС + ДС = 46,3
Р3 = ДС + СА + АД = 39,9
Красное число хода равно длине хода, деленное на периметр полигона.
Так для первого полигона
Кр.АВ1 = 21,2/37 = 0,57
Кр.АД1,3 = 9,2/37 = 0,25
Кр.ВД1,2 = 6,6/37 = 0,18
Для второго полигона
Кр.ВС2 = 18,6/46,3 = 0,40
Кр.ВД2,1 = 6,6/46,3 = 0,14
Кр.СД2,3 = 21,1/46,3 = 0,46
Для третьего полигона
Кр.АС3 = 9,6/39,9 = 0,24
Кр.СД3,2 = 21,1/39,9 = 0,53
Кр.АД3,1 = 9,2/39,9 = 0,23
Красные числа обозначаем красным цветом над соответствующими рамками, расположенными вне полигона около его звеньев.
Контроль. Для каждого полигона сумма красных чисел должна быть равна единице.
0,57 + 0,25 + 0,18 = 1; 0,40 + 0,14 + 0,46 = 1; 0,24 + 0,53 + 0,23 = 1
Распределение невязок в полигонах производят пропорционально красным числам звеньев, начиная с полигона с наибольшей по абсолютному значению невязкой. ( полигон III, т.к. WIII = -54)
Поправка, приходящая на звено, определяется как произведение невязки полигона на красное число звена:
VIII = WIII* Кр.АС3 = -54*0,24 = -13
VIII,I = WIII* Кр.АД3,1 = -54*0,23 = -12
VIII,II = WIII* Кр.СД3,2 = -54*0,53 = -29
Контроль: сумма поправок равна невязке полигона:
Полученные поправки по звеньям записываем в соответствующие рамки.
В следующем полигоне значение исходной невязки +37мм. изменится на величину поправки, перешедшей из третьего полигона:
WI’ = WI + VIII,I = 37 + (-12) = +25
Новую невязку так же распределяют по звеньям пропорционально красным числам и подписывают во внешних к полигону рамках под соответствующими красными числами.
Во втором полигоне новая невязка равна сумме начальной невязке и поправок, перешедших из третьего и первого полигонов.
WII’ = WII + VIII,II + VI,II = -17+ 5 +(-29) = -41
Полученную невязку распределяем так же по аналогии.
Приступаем ко второму циклу:
В третьем полигоне образуется новая невязка, равная сумме поправок, перешедших из смежных полигонов
WIII’ = VII,III + VI,III = -19 + 6 = -13
Невязку распределяем по аналогии.
В первом полигоне так же образуется новая поправка, равная сумме поправок смежных полигонов
WI’ = VIII,I + VII,I = -3 — 6 = -9
Далее по аналогии.
Циклы распределения продолжаются до тех пор, пока невязки всех полигонов не станут равными нулю.
Подсчитываем суммы чисел во всех рамках .
Контролем правильности распределения невязки служит равенство суммы чисел в рамочках поправок у внешних и внутренних звеньев и суммы чисел в рамочке невязок, соответствующего полигона.
Затем вычисляем поправки на звенья каждого полигона, считая направления звеньев совпадающими с направлением обхода полигона. При этом руководствуемся следующими правилами:
Для внешнего звена полигона поправка на звено равна сумме поправок внешней рамочки этого звена с обратным знаком. V1 = +7, V2 = +21, V3 = +19
Для звеньев смежных полигонов поправка равна разности сумм чисел внутренней и внешней табличек этого звена.
Для первого полигона: V1,2 = -8-3 = -11
Для второго полигона: V2,1 = +3-(-8) = +11
Для третьего полигона: V3,1 = +3-(-16) = +19
Контролем уравнивания сети является выполнение условия: в каждом полигоне сумма поправок на звенья должна равняться невязке полигона с обратным знаком. Допуск 1мм.
Источник
