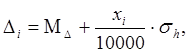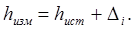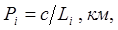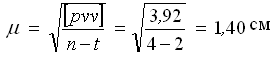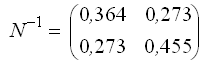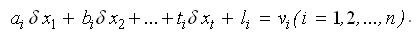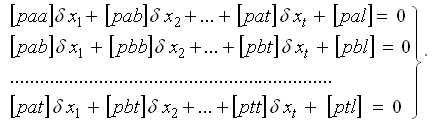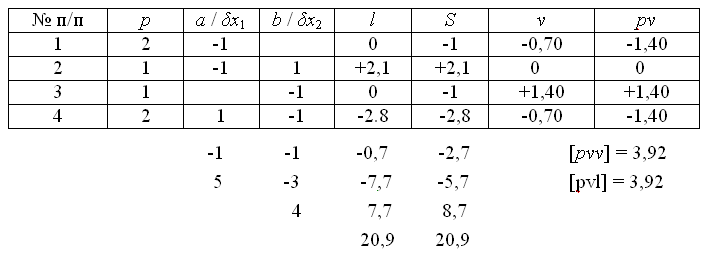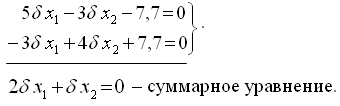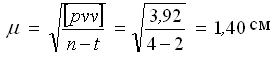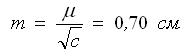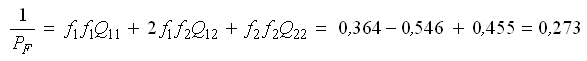Уравнивание нивелирных сетей (Глава 2 дипломного проекта) , страница 5
2) Вычислены истинные ошибки результатов измерений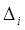 
по формуле
где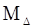 
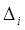
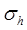
— математическое ожидание случайной ошибки ,
-среднее квадратическое отклонение измеренного превышения,
xi взяли из таблиц нормально распределенных случайных чисел /5/:
1,393 -1,783 -0,105 -1,339 1,041 0,279 -1,805 -1,186
3) Вычислены измеренные значения превышений
4) Вычислены веса результатов измерений
Результаты моделирования приведены в таблице 3:
Моделирование нивелирной сети
, см
Источник
3.8. Уравнивание нивелирной сети параметрическим способом
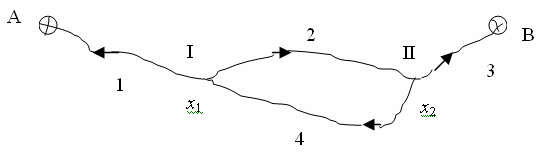
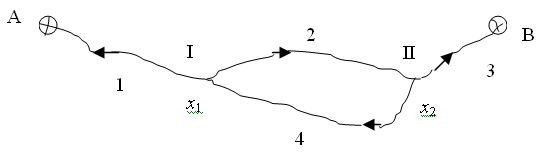
Рис. 3. Нивелирная сеть
НА = 100,000 м; НВ = 115,000 м — отметки исходных пунктов.
h (м): 5,023; 10,012; 9,990; -10,005 — измеренные превышения.
S (км): 2; 4; 4; 2 — длины ходов.
pi = c/Si: 2; 1; 1; 2 — веса результатов измерений (с = 4 ).
В данной нивелирной сети число измерений n = 4, число необходимых измерений t = 2. Два параметра х1 и х2 — отметки вновь определяемых пунктов.
Параметрические уравнения связи составим по формуле:
Fi(x1, x2, . xt) — yi = νi.
1) (HA — x1) — h1 = ν1; 3) (HB — x2) — h3 = ν3;
2) (x2 — x1) — h2 = ν2; 4) (x1 — x2) — h4 = ν4
— параметрические уравнения связи.
Определим приближенные значения параметров:
х01 = НА — h1 = 94,977 м; x02 = HB — h3 = 105,010 м.
x1 = х01 + δх1 и x2 = x02 + δx2 подставим в систему параметрических уравнений связи.
1) (HA — x01 — δx1) — h1 = ν1; 3) (HB — x02 — δx2) — h3 = ν3;
2) (x02 + δx2 — x01 — δx1) — h2 = ν2; 4) (x01 + δx1 — x02 — δx2) — h4 = ν4.
Переходим к параметрическим уравнениям поправок:
Свободные члены li = Fi(x10, x20, . xt0) — yi, (i = 1, 2, . n) выразим в сантиметрах или в миллиметрах для того, чтобы порядок коэффициентов и свободных членов был одинаков.
1) -δx1 + l1 = v1; l1 = HA — x01 — h1 = 0;
2) δx2 — δx1 + l2 = v2; l2 = x02 — x01 — h2 = 2,1 см;
3) -δx2 + l3 = v3; l3 = HB — x02 — h3 = 0;
4) δx1 — δx2 + l4 = v4; l4 = x01 — x02 — h4= -2,8 см.
Переходим к системе нормальных уравнений:
Коэффициенты и свободные члены параметрических уравнений поправок поместим в табл. 10.
Таблица параметрических уравнений поправок
Система нормальных уравнений имеет вид:
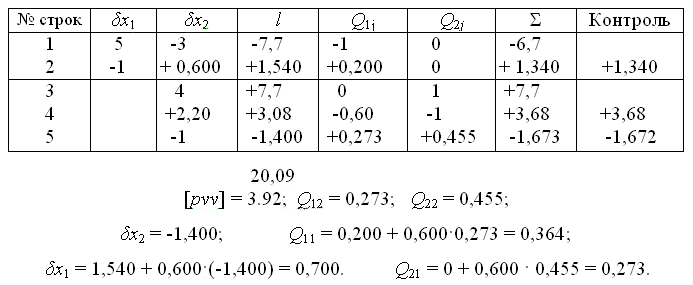
Решение системы нормальных уравнений с определением элементов обратной матрицы выполним в схеме Гаусса (табл. 10).
Решение нормальных уравнений
Контроль δхj: Контроль Qij: 2 · 0,364 + 0,273 — 1 = 0,001;
2 · 0,700 — 1,400 = 0. 2 · 0,273 + 0,455 — 1 = 0,001.
Вычислим значение параметров:
x1 = x10 + δx1 = 94,9840 м; x2 = x20 + δx2 = 104,9960 м.
Вычислим уравненные результаты измерений, делаем контроль уравнивания (табл. 12).
Уравненные превышения. Контроль уравнивания
Сделаем оценку точности результатов измерений по материалам уравнивания:
— средняя квадратическая ошибка единицы веса (превышения по ходу в 4 км).
— средняя квадратическая ошибка на 1 км хода.
Оценку точности параметров и функции параметров выполним с использованием элементов обратной матрицы
по формулам (38) и (37):
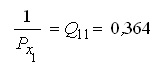
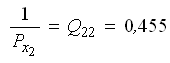
— обратный вес первого параметра.
см — средняя квадратическая ошибка первого параметра.
— обратный вес второго параметра.
см — средняя квадратическая ошибка второго параметра.
— весовая функция — второе уравненное превышение.
— коэффициенты функции.
— обратный вес функции.
см — средняя квадратическая ошибка функции.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Уравнивание нивелирной сети параметрическим способом
Рис. 3. Нивелирная сеть
НА = 100,000 м; НВ = 115,000 м — отметки исходных пунктов.
h (м): 5,023; 10,012; 9,990; -10,005 — измеренные превышения.
S (км): 2; 4; 4; 2 — длины ходов.
pi = c/Si: 2; 1; 1; 2 — веса результатов измерений (с = 4 ).
В данной нивелирной сети число измерений n = 4, число необходимых измерений t = 2. Два параметра х1 и х2 — отметки вновь определяемых пунктов.
Параметрические уравнения связи составим по формуле:
— параметрические уравнения связи.
Определим приближенные значения параметров:
x1 = х 0 1 + δх1 и x2 = x 0 2 + δx2 подставим в систему параметрических уравнений связи.
Переходим к параметрическим уравнениям поправок:
Свободные члены li = Fi(x1 0 , x2 0 , . xt 0 ) — yi, (i = 1, 2, . n) выразим в сантиметрах или в миллиметрах для того, чтобы порядок коэффициентов и свободных членов был одинаков.
Переходим к системе нормальных уравнений:
Коэффициенты и свободные члены параметрических уравнений поправок поместим в табл. 10.
Таблица параметрических уравнений поправок
Система нормальных уравнений имеет вид:
Решение системы нормальных уравнений с определением элементов обратной матрицы выполним в схеме Гаусса (табл. 10).
Решение нормальных уравнений
Контроль δхj: Контроль Qij: 2 · 0,364 + 0,273 — 1 = 0,001;
2 · 0,700 — 1,400 = 0. 2 · 0,273 + 0,455 — 1 = 0,001.
Вычислим значение параметров:
Вычислим уравненные результаты измерений, делаем контроль уравнивания (табл. 12).
Уравненные превышения. Контроль уравнивания
| № п/п | hi + vi | F(x1, x2) | № п/п | hi + vi | F(x1, x2) |
| 5,0160 | НА — х1 | 5,0160 | 10,0040 | НВ — х2 | 10,0040 |
| 10,0120 | х2 — х1 | 10,0120 | -10,0120 | х1 — х2 | -10,0120 |
Сделаем оценку точности результатов измерений по материалам уравнивания:
— средняя квадратическая ошибка единицы веса (превышения по ходу в 4 км).
— средняя квадратическая ошибка на 1 км хода.
Оценку точности параметров и функции параметров выполним с использованием элементов обратной матрицы
по формулам (38) и (37):
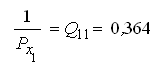
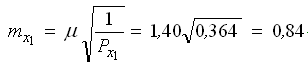
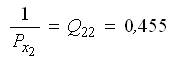
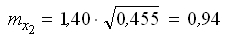
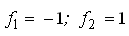
— обратный вес первого параметра.
см — средняя квадратическая ошибка первого параметра.
— обратный вес второго параметра.
см — средняя квадратическая ошибка второго параметра.
— весовая функция — второе уравненное превышение.
— коэффициенты функции.
— обратный вес функции.
см — средняя квадратическая ошибка функции.
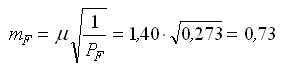
Источник
Сущность параметрического способа уравнивания
При уравнивании геодезических сетей параметрическим способом первоначально выбираются так называемые параметры, через которые посредством уравнений связи выражается каждая измеренная величина. Поэтому непосредственно уравниваемыми величинами являются параметры, а затем уже по уравненным значениям параметров вычисляются уравненные значения непосредственно измеренных величин..
Пусть в геодезической сети измерено 
величин 
, 
, …, 
, из которых 
величин являются избыточно измеренными. Далее выбирается ряд независимых неизвестных параметров 
, 
, …, 
, через которые могут быть выражены значения измеренных величин 
, ( 
). Число 
таких параметров должно быть равно числу избыточно измеренных величин. Каждая избыточно измеренная величина в геодезической сети приводит к возникновению одного уравнения связи вида
, ( ) , (7.43)
где , ( ) – истинные значения измеренных величин;
, ( 
) – истинные значения параметров.
Уравнения (7.43) называются параметрическими уравнениями связи в общем виде .
Как уже ранее отмечалось, целью уравнительных вычислений является вычисление таких поправок 
в измеренные величины 
, при которых удовлетворялись бы все существующие зависимости между элементами сети, причем не только измеренными, но и вычисляемыми. Это означает, что если в левой части выражений (7.43) поставить уравненные значения измеренных величин, то должны измениться и правые части, а именно, должны измениться значения параметров 
, т.е. в правой части должны стоять соответствующие уравненные значения параметров.
(7.44)
уравненные значения измеренных величин, а через
(7.45)
уравненные значения параметров, где 
– приближенные значения неизвестных параметров , а 
– поправки к приближенным значениям параметров. Тогда система уравнений (7.43) может быть переписана в виде
, ( ) , (7.46)
, (7.44)
1. Гудков В.М., Хлебников А.В. Математическая обработка маркшейдерско-геодезических измерений. Учеб. для вузов. – М.: Недра, 1990.– 335 с.
2. Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений. – М.: Недра, 1977. 387 с.
3. Смолич Б.А. Уравнительные вычисления. Учеб. для техникумов – М.: Недра, 1989. – 245 с.
4. Мазмишвили А.И. Теория ошибок и метод наименьших квадратов. – М.: Недра, 1978. 311 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.1 – М.: Недра, 1970. 456с.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб. для втузов. Т.2 – М.: Недра, 1970. 576с.
7. Бермант А.Ф. Курс математического анализа. Часть 1. – М.: Госуд. изд-во физ-мат. литературы. 1959, 466 с.
8. Селиханович В.Г. Геодезия. Учеб. для вузов.Ч. II – М.: Недра, 1981. 544 с.
Источник
