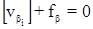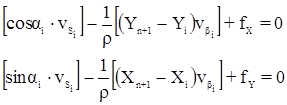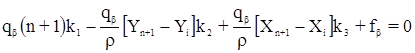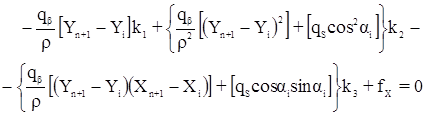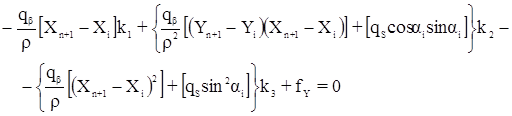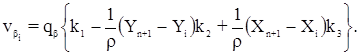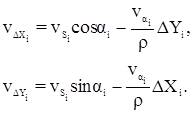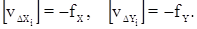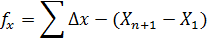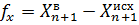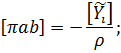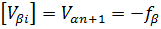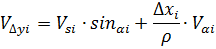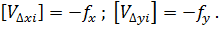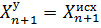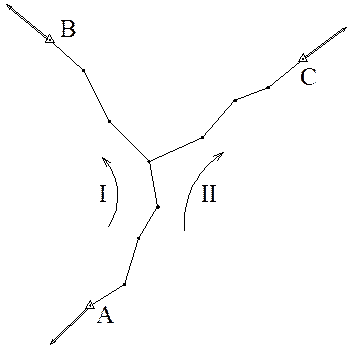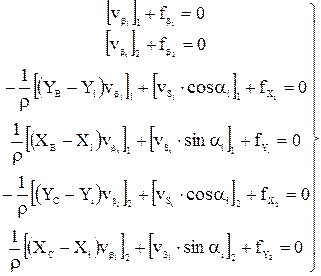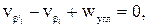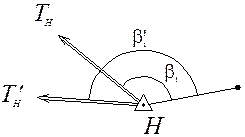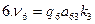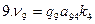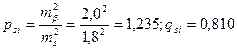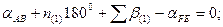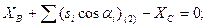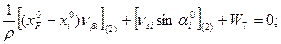Уравнение коррелатным способом полигонометрического хода

Уравнивание коррелатным способом хода, опирающегося на исходные пункты и направления

Рассмотрим схему хода (рис. 19.1). В таком ходе общее измерение составляет п – линий и п + 1 углов, т.е. всего (2п + 1) измерений. Количество необходимых измерений составляет 2(п – 1). следовательно, число избыточных измерений r = (2n + 1) — 2(п – 1) = 3.

Рисунок 19.1 – Схема полигонометрического хода

Возникают три условных уравнения поправок:

Эти уравнения имеют вид:

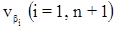
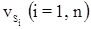
где – поправки в измеренные углы;

– поправки в измеренные длины линий;

X_i, Y_i (i = Нач, 1,2, …, n-1, Кон) – координаты текущей точки хода, в которой измерен угол b_i;

X_n, Y_n – координаты конечной точки хода.

При этом a_i, f_X, f_Y вычисляются без предварительного распределения угловой невязки. Для упрощения вычислений координаты пунктов полигонометрии могут вычисляться в условной системе, когда координаты начального пункта приравниваются к нулю.

Система нормальных уравнений коррелат имеет вид:

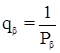
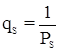
Здесь — обратный вес измеренных углов, — обратные веса измеренных длин линий. В результате решения нормальных уравнений определяют коррелаты k₁, k₂ и k₃. Поправки в измеренные углы вычисляются по формуле:

Контроль: .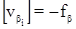

Поправки в измеренные длины линий вычисляются по формуле:

.

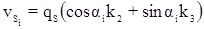
Поправки в предварительные значения дирекционных углов вычисляются по формуле:

.

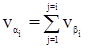
Уравненные углы, дирекционные углы и длины линий находят введением поправок v_b, v_a и v_S в значения b, a и S. Уравненные значения приращений координат вычисляют по уравненным дирекционным углам и длинам линий:

.

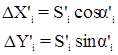
Кроме того, поправки в приращения координат можно вычислить по формуле:

Контроль:

В этом случае уравненные приращения координат вычисляются по формулам:

.

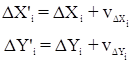
Уравненные координаты пунктов полигонометрического хода вычисляются по формулам:

Источник

20 Уравнивание коррелатным способом полигонометрического хода

Перевод градусы, минуты, секунды в доли градуса:

Перевод доли_Градусы в градусы, минуты, секунды

Секунды=(((Доли_Градусы- Градусы)*60)- Минуты)*60

Вычисления угловой невязки

; ; ;

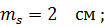
Вычисления невязки по абсциссе и ординате

Вычисления условных координат

Нормальные уравнения коррелат

;

Решение нормальных уравнений коррелат

Вычисления уравненных координат

Вычисление средней квадратической ошибки единицы веса

,

где .

21. Сущность и теоретическая основа параметрического способа уравнивания.

Параметрический способ уравнивания по МНК предполагает использование параметрических уравнений с представлением всех измеренных величин в виде функций независимых параметров. Пусть выполнено n измерений у1, у2, …, уn с весами p1, p2, …, pn, t – число необходимых измерений.

Выбирают t параметров (независимых неизвестных) – х1, х2, …, хt. Это могут быть измеряемые и не измеряемые (отметки, координаты определяемых пунктов) величины. Если Y1, Y2, …, Yn – истинные значения измеренных величин, а Х1, Х2, …, Хt – точные значения параметров, то между этими значениями может быть установлена исходная система параметрических уравнений связи: Fi(X1, X2, …, Xt) = Yi (i = 1, 2, …, n).

С уравненными значениями измеренных величин и параметров система принимает вид: Fi(x1, x2, …, xt) = yi + vi (i = 1, 2, …, n) или Fi(x1, x2, …, xt) – yi = vi (i = 1, 2, …, n).

Функции Fi приводят к линейному виду разложением в ряд Тейлора. С этой целью вводят приближенные значения, которые вычисляют по результатам измерений.

22 Порядок контроля и приемки геодезических и топографических работ Задачами контроля всех видов работ яв-ся:

Проверка соответствия процессов, а так же результатов выполняемых работ и их оформления, проектов и действующих нормативных актов.

Выявление степени завершенности работ

Проверка полноты использования геодезических, аэрофотосъемочных, картографических и справочных материалов.

Представление объектных данных для оценки качества работ

Предупреждение брака, а работе, оказание необходимой помощи, при выполнении работ в у3словненные сроки и с соблюдением условленных требований.

Проверка состояния приборов и вспомогательных принадлежностей, правильности их эксплуатации и хранения.

Приемка геодезических и топографических работ:

Основной задачей внутриведомственной приемки яв-ся принятие решения о соответствии ее фактических параметров (объема, точности) техническим документам предприятия, по которым происходит сдача – приемка продукции.

Приемка продукции происходит на основе приемочного контроля, но может базироваться и на результатах ранее выполненных процедур контроля, эти результаты оформляют, в случае необходимости, как данные приемочного контроля.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Уравнивание полигонометрической сети коррелатным способом

Число условий, возникающих в сети, определяется по формуле:

где N – число замкнутых полигонов;

Т – число исходных пунктов в сети.

Если на узловых пунктах были измерены (определены по астрономическим или гироскопическим наблюдениям) дирекционные углы, то:

где Q – количество измеренных дирекционных углов в узловых пунктах.

Из всех условий будем иметь r_α условий дирекционных углов и r_X,Y условий координат. Кроме того, в сети могут возникать условия горизонта и твердого угла. Для составления условных уравнений поправок по схеме сети намечают замкнутые и разомкнутые полигоны, опирающиеся на исходные пункты. При этом все полигоны должны быть независимыми и все ходы должны быть включены в полигоны. Намеченные полигоны нумеруют, а их направление показывают стрелкой (рис.20.1).

Рисунок 20.1 – Схема полигонометрической сети

т.е. в такой системе 6 условных уравнений, из которых 2 – дирекционных углов и 4 – координат.

Эти уравнения имеют вид:

Если в сети измерялись по два примычных угла в исходных пунктах (рис. 20.2), то условные уравнения поправок угла имеют вид:

Рисунок 20.2 – Схема примыкания к двум пунктам

Эти условия необходимо составлять не только для контроля, но и включать их в уравнивание, т.к. это повышает вес уравненных элементов сети. Аналогично поступают с условием горизонта, когда в узловом пункте измерены не только необходимые углы, но и углы, замыкающие горизонт.

От условных уравнений в соответствии с принципом наименьших квадратов переходят к системе нормальных уравнений коррелат, число которых равно числу условий. По найденным из решения нормальных уравнений коррелатам определяют поправки в углы и длины линий. Дальнейший процесс уравнивания и оценки точности полигонометрической сети такой же, как и при уравнивании отдельного полигонометрического хода.

Дата добавления: 2016-06-02 ; просмотров: 1365 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Примеры коррелатного способа уравнивания

В этом разделе приводятся примеры уравнивания некоторых геодезических построений. В примерах рассматривается алгоритм решения задачи уравнивания для разных вариантов геодезических построений со сравнительно небольшим числом измеренных величин, как это часто имеет место, например, в практике геодезических и маркшейдерских работ на земной поверхности при создании опорных сетей либо в горных выработках при обработке результатов измерений в системах полигонометрических ходов. Уравнивание систем нивелирных ходов обычно производится при точных и высокоточных измерениях, например, при наблюдениях за деформациями горных выработок и наземных сооружений, что тоже имеет место и в практике геодезических и маркшейдерских работ.

В примерах рассмотрены сравнительно простые схемы геодезических построений, однако принцип расчётов и в сложных системах точно такой же, как и в простых.

137.1. Уравнивание углов в полигоне

В полигоне, состоящем из четырёх вершин (рис. 14.7), неравноточно измерены горизонтальные углы: А = β₁ , В = β₂ , С = β₃ , D = β₄ (табл. 14.4).

Выполнить уравнивание углов без учёта измерения длин сторон.

Предварительно найдем веса p_i и обратные веса q_i, приняв м (см. табл. 14.4) без учёта величин измеренных углов, считая их практически примерно одинаковыми (значения весов определяются по условию возможной погрешности в направлениях из-за центрирования теодолита; для веса угла применяется правило сложения обратных весов направлений):

, (14.91)

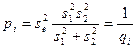
где s₁ и s₂ – стороны, образующие данный угол.

Шаг 1. Общее число измеренных величин n = 4, число необходимых измерений k = 3, число избыточных измерений r = 1.

Шаг 2. Составим условное уравнение (условие сумм углов полигона).

Всего одно уравнение, поскольку r = 1.

Шаг 3. Приводим условное уравнение к линейному виду, для чего продифференцируем его и найдем частные производные функции по аргументам β_i . Очевидно, что

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (таблица 14.5).

Рис. 14.7. Уравнивание углов в полигоне.

Обозначение	Значение угла	Вес pi	Обратный вес qi
β1	80 0 16′ 44,3″	0,221	4,520
β2	91 0 45′ 00,7″	0,459	2,181
β3	69 0 25′ 56,8″	0,473	2,113
β4	118 0 32′ 25,2″	0,225	4,452

Матрица коэффициентов, весов и обратных весов

i→ j↓
+ 1	+ 1	+ 1	+ 1
рi	0,221	0,459	0,473	0,225
qi	4,520	2,181	2,113	4,452

Свободный член уравнения

Шаг 4. Найдём коэффициенты b_jj нормальных уравнений (в данном случае – уравнений коррелат):

, (14.92)

. (14.93)

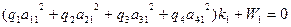
Для приведенного примера, с учётом значений a_ij и q_i , 13,266 k₁ + 7 = 0, откуда k₁ = — 0,528.

Шаг 5. Составляем условное уравнение поправок

(14.94)

и формулы для вычисления поправок (с вычислением их значений):

Контроль по формуле (14.94): условие выполнено! (проверьте сами). Отступление при округлениях значений поправок на 0,1″ является допустимым.

Вспомните загадку, которая прозвучала в начале этой главы. А если забыли, то возвратитесь к этому началу. Вот оно, что «под конец тонко» — это и есть хвостик решения всей задачи уравнивания: маленькие поправочки в измеренные величины. Ну а что тут было зелено, да посерёдке толсто – это уж понятно из решения данной задачи. Правда, приведенная задача – одна из самых простых. Дальше будет корнеплод посложнее. Но, всему своё время. А сейчас – закончим решение приведенной задачи.

Шаг 6. Вычисляем уравненные значения углов:

β₁ ‘ = 80° 16′ 44,3″ – 2,4″ = 80° 16′ 41,9″; β₂ ‘ = 91° 45′ 00,7″ – 1,1″ = 91° 44′ 59,6″;

β₃ ‘ = 69° 25′ 56,8″ – 1,2″ = 69° 25′ 55,6″; β₄ ‘ = 118° 32′ 25,2″ – 2,4″ = 181° 32′ 22,8″.

Контроль: подстановка уравненных значений углов в уравнение (14.91) – условие выполнено! (проверьте это условие).

Очевидно, что при равноточных измерениях углов для них были бы получены одинаковые поправки, т.е. невязка была бы распределена поровну во все углы.

137.2. Уравнивание системы нивелирных ходов с несколькими узловыми точками

На местности пройдена система нивелирных ходов с четырьмя узловыми точками 1, 2, 3 и 4 (рис. 14.8). В результате измерений образовано 9 секций, превышения в которых по указанному направлению приведены непосредственно на схеме. Указаны также высоты исходных реперов Р10, Р20 и Р30. В табл. 14.6 приведены длины ходов в секциях и значения весов и обратных весов превышений в секциях, вычисленные по формулам:

Рис. 14.8. Схема нивелирных ходов с четырьмя узловыми точками.

№ секции	Превышение h, мм	Длина хода s в секции, км	Вес p пре-вышения	Обратный вес q пре-вышения
+3586	0,84	2,38	0,42
+2841	1,36	1,47	0,68
-752	2,15	0,93	1,08
-1243	0,78	2,56	0,39
+509	2,63	0,76	1,32
+5338	2,05	0,98	1,03
-5863	3,02	0,66	1,51
+4639	3,44	0,58	1,72
-3024	2,38	0,84	1,19

, (14.95)

где

Требуется определить уравненные значения высот узловых точек.

Шаг 1. Общее число измерений n = 9, число необходимых измерений k = 4, число избыточных измерений r = 5.

Шаг 2. Составим r = 5 условных уравнений:

Шаг 3. Приведём условные уравнения к линейному виду, продифференцировав их по аргументам h_i. Получим коэффициенты a_ij условных уравнений поправок:

Составим матрицу коэффициентов a_ij со строкой обратных весов q_i (табл. 14.7).

Матрица коэффициентов и обратных весов

→ i j↓
+1	-1	+1
-1	+1	+1
+1	+1	+1
+1	+1	-1
+1	+1	+1
qi	0,42	0,68	1,08	0,39	1,32	1,03	1,51	1,72	1,19

Вычислим свободные члены (в мм), подставив в уравнения (14.96) измеренные значения h_i в секциях:

Шаг 4. Найдём по формулам (14.88) коэффициенты b_jj нормальных уравнений коррелат:

(14.97)

После подстановки значений a_ij и q_i в уравнения (14.97) получим исходные нормальные уравнения коррелат:

Из решения системы уравнений (14.98) одним из способов получим:

Контроль вычисления коррелат выполняем подстановкой их значений в исходные уравнения (14.98):

1. 2,18 (-2,137) – 1,08 (-11,552) + 0,42 (-1,945) – 7 = + 0,001;

2. -1,08(-2,137) + 2,79(-11,552) + 1,32(+9,606) + 0,39(-1,945) + 18 = -0,001;

3. 1,32(-11,552) + 3,86(+9,606) + 1,51(-3,882) – 16 = — 0,031;

4. 1,51(+9,606) + 4,42(-3,882) + 1,72(-1,945) + 6 = +0,001;

5. 0,42(-2,137) + 0,39(-11,552) + 1,72(-3,882) + 2,53(-1,945) + 17 = -0,001.

Сравнительно большее невыполнение условия мы видим в уравнении 3. Это вызвано погрешностями округлений. При вычислении с большими значащими цифрами этого не наблюдалось бы. При этом результаты вычислений принимаем удовлетворительными, поскольку поправки в измеренные значения превышений для данных условий будут в дальнейшем округляться до 1 мм, а вычисления проведены с большим запасом точности.

Шаг 5. Составляем условные уравнения поправок v_i, пользуясь формулами (14.86) и табл. 14.7:

(14.99)

1. v₁ = 0,42 ∙1∙ (-2,137) + 0,42∙1∙ (-1,945) = — 1,714 = — 2 мм;

2. v₂ = 0,68 ∙ (-1) ∙ (-2,137) = + 1,453 = + 1 мм;

3. v₃ = 1,08 ∙ 1 ∙ (2,137) + 1,08 ∙ (-1) ∙ (-11,552) = +10,168 = + 10 мм;

4. v₄ = 0,39 ∙ 1 ∙ (-11,552) + 0,39 ∙1 ∙ (-1,945) = — 5,264 = — 5 мм;

5. v₅ = 1,32 ∙1∙ (-11,552) + 1,32 ∙ 1 ∙ (+9,606) = — 2,569 = — 3 мм;

6. v₆ = 1,03 ∙1 ∙ (+9,606) = + 9,894 = + 10 мм;

7. v₇ = 1,51 ∙ 1 ∙ (+9,606) + 1,51 ∙1 ∙ (-3,882) = + 8,643 = + 9 мм;

8. v₈ = 1,72 ∙ 1 ∙ (-3,882) + 1,72 ∙ 1 ∙ (-1,945) = — 10,022 = — 10 мм;

9. v₉ = 1,19 ∙ (-1) ∙ (-3,882) = + 4,620 = + 5 мм.

Контроль вычисления поправок можно выполнить по формулам (14.96), подставив в них вместо превышений значения поправок (суммы поправок должны быть равны значениям соответствующих невязок с обратным знаком):

Шаг 6. Вычисляем уравненные значения превышений в секциях и контролируем уравнивание по выполнению условия (14.96):

h₆ ‘= + 5338 + 10 = + 5348 мм;

Подстановка в уравнения (14.96) подтверждает выполнение указанного условия.

Вычисляем уравненные значения высот узловых точек 1, 2 , 3 и 4:

Контроль вычислений здесь можно выполнить вторичным получением высот искомых точек по другим направлениям. Должны получиться те же результаты. Например, H₁ = H_P30 – h₈‘ – h₄‘ = 85,301 – 4,629 + 1,248 = 81,920 м.

137.3. Уравнивание системы полигонометрических ходов с двумя узловыми точками

Уравнивание таких систем полигонометрических ходов аналогично уравниванию как одиночного полигонометрического хода, так и системы полигонометрических ходов с одной узловой точкой. В такой системе (рис. 14.9) образуется три независимых полигонометрических хода [(1), (2), (3)], в которых возникает по три условия: три условия дирекционных углов и шесть условий координат, т.е. получается девять условных уравнений.

Рис. 14.9. Система полигонометрических ходов с двумя узловыми точками.

В табл. 14.8, 14.9 и 14.10 приведены необходимые исходные данные для решения задачи уравнивания, заключающейся в определении уравненных значений координат точек 1, 2, 3, M, N, а также уравненного значения дирекционного угла узловой линии MN. (В данном примере узловые точки M и N образуют и узловую линию).

Часто между узловыми точками прокладывают полигонометрический ход в две и более линии. Тогда понятие узловой линии не будет иметь места. Ею может быть любая линия с началом в какой-либо узловой точке).

Горизонтальные углы измерены равноточно с погрешностью m_β = 2,0″. Расстояния измерены светодальномером с погрешностью, примерно одинаковой для всех линий (m_s = 18 мм = 1,8 см). В соответствии с указанной точностью измерения расстояний и углов веса углов принимаем равными единице (p_β = 1; q_β = 1), а веса расстояний –

Координаты исходных пунктов

Координаты, м	B	C	F	G
Х	7183,652	8137,565	6124,924	7894,521
Y	4380,124	6463,782	4718,048	7173,596

Исходные дирекционные углы

αАВ	71º 08′ 14,3″	α BA	251º 08′ 14,3″
α CD	118º 19′ 14,7″	α DC	298º 19′ 14,7″
α EF	324º 21′ 18,0″	α FE	144º 21′ 18,0″
α GH	159º 58′ 14,2″	α HG	339º 58′ 14,2″

Измеренные горизонтальные углы и расстояния

Обозначение угла	Значение угла	Обозначение расстояния	Значение расстояния, м
β 1	226º 15′ 25″	s 1	475,885
β 2	201º 36′ 36″	s 2	693,027
β 3	85º 02′ 31″	s 3	857,338
β 4	170º 15′ 07″	s 4	401,239
β 5	172º 53′ 18″	s 5	841,215
β 6	271º 07′ 58″	s 6	625,329
β 7	280º 34′ 07″	s 7	573,421
β 8	84º 46′ 52″	s 8	989,716
β 9	337º 03′ 44″
β 10	178º 54 26″
β 11	78º 21 28″

Выполним предварительные вычисления в полигонометрических ходах (1), (2) и (3), т.е. определим координаты точек ходов, используя только измеренные величины (табл. 14.11).

Шаг 1. Общее число измерений n = 19 (11 углов и 8 расстояний), число необходимых измерений k = 10, число избыточных измерений r = 9.

№№ точек	Гориз.углы β	Дирекц.углы α	Рассто-яния s , м	Приращения координат, м	Координаты, м	№№ точек
Δх	Δу	Х	Y
A	Ход (1)
71°08’14,3″
B	226°15’25»	7183,652	4380,124	B
117°23’39,3″	475,885	-218,960	+422,520
201°36’36»	6964,692	4802,644
139°00’15,3″	693,027	-523,068	+454,628
M	280°34’07»	6441,624	5257,272	M
239°34’22,3″	625,329	-316,693	-539,205
F	84°46’52»	6124,931 6124,924 +0,7 см	4718,067 4718,048 +1,9 см	F o FИСХ
144°21’14,3″ 144°21’18,0″ -3,7″
E
Ход (2)
A
71°08’14,3″
B	226°15’25»	7183,652	4380,124	B
117°23’39,3″	475,885	-218,960	+422,520
201°36’36»	6964,692	4802,644	1
139°00’15,3″	693,027	-523,068	+454,628
M	85°02’31»	6441,624	5257,272	M
44°02’46,3″	857,338	+616,237	+596,054
N	170°15’07»	7057,861	5853,326	N
34°17’53,3″	401,239	+331,470	+226,098
172°53’18»	7389,331	6079,424
27°11’11,3″	841,215	+748,281	+384,341
C	271°07’58»	8137,612 8137,565	6463,765 6463,782	C o СИСХ
118°19’09,3″ 118°19’14,7″ -5,4″
D	+4,7 см	-1,7 см
Ход (3)
H
339°58’14,2″
G	78°21’28»	7894,521	7173,596	G
238°19’42,2″	573,421	-301,075	-488,022
178°54’26»	7593,446	6685,574
237°14’08,2″	989,716	-535,620	-832,255
N	337°03’44»	7057,826	5853,320	N
34°17’52,2″	401,239	+331,471	+226,096
172°53’18»	7389,297	6079,415
27°11’10,2″	841,215	+748,283	+384,337
C	271°07’58»	8137,580 8137,565	6463,752 6463,782	C o СИСХ
118°19’08,2″ 118°19’14,7″ -6,5″
D	+1,5 см	-3,0 см

Шаг 2. Составление условных уравнений.

Для трёх независимых ходов, будем иметь три условных уравнения для дирекционных углов и шесть условных уравнений для координат ( три – для абсцисс, три – для ординат).

1.

2.

3.

4.

5. (14.100)

6.

7.

8.

9.

В уравнениях (14.100) индексы (1), (2) и (3) относятся к соответствующим ходам (см. табл. 14.11), например, n₍₁₎ = 4, n₍₂₎ = 6, n₍₃₎ = 5.

Приведём условные уравнения к линейному виду по правилам, изложенным выше. В полученные выражения введём знак гауссовых сумм.

1.

2.

3.

4.

5. (14.101)

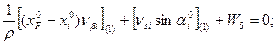
6.

7.

8.

9.

В уравнениях (14.101) значения координат берут в километрах, а значение ρ = 206265″ уменьшают на 100000.

Вычислим значения невязок в уравнениях (14.101) с учётом данных измерений и предварительных вычислений:

где T_i o – результат вычисления исходной величины T_i(исх).

W₁ = 144º 21′ 14,3″ – 144º 21′ 18,0″ = — 3,7″ ;

W₂ = 118º 19′ 09,3″ – 118º 19′ 14,7″ = — 5,4″ ;

W₃ = 118º 19′ 08,2″ – 118º 19′ 14,7″ = — 6,5″ ;

W₄ = 6124,931 – 6124,924 = +0,007 м = + 0,7 см;

W₅ = 4718,067 – 4718,048 = + 0,019 м = + 1,9 см;

W₆ = 8137,612 – 8137,565 = + 0,047м = + 4,7 см;

W₇ = 6463,765 – 6463,782 = — 0,017 м = — 1,7 см;

W₈ = 8137,580 – 8137,565 = + 0,015 м = + 1,5 см;

W₉ = 6463,752 – 6463,782 = — 0,030 м = — 3.0 см .

По данным табл. 14.11 составим табл. 14.12 значений синусов и косинусов дирекционных углов и разностей абсцисс и ординат. Получим окончательные условные уравнения поправок:

Значения синусов и косинусов дирекционных углов, значения разностей координат

№№ точек	Sin αi	Cos αi	(хn 0 -xi 0 ), км	(yn 0 -yi 0 ), км
Ход 1
В	(В-1) 0,8879	-0,4601	-1,0587	0,3379
(1-М) 0,6560	-0,7548	-0,8398	-0,0846
М	(M-F) -0,8623	-0,5064	-0,3167	-0,5392
F
Ход 2
В	(В-1) 0,8879	-0,4601	0,9540	2,0836
(1-М) 0,6560	-0,7548	1,1729	1,6611
М	(M-N) 0,6952	0,7188	1,6960	1,2065
N	(N-2) 0,5635	0,8261	1,0798	0,6104
(2-C) 0,4569	0,8895	0,7483	0,3843
C
Ход 3
G	(G-3)-0,8511	-0,5250	0,2431	-0,7098
(3-N)-0,8409	-0,5412	0,5441	-0,2218
N	(N-2)0,5635	0,8261	1,0798	0,6104
(2-C)0,4569	0,8895	0,7483	0,3843
C

Составим матрицу коэффициентов a_ij и обратных весов q_i , необходимую для определения коэффициентов нормальных уравнений коррелат (табл. 14.13).

Матрица коэффициентов и обратных весов

i→ j↓	β1	β2	β3	β4	β5	β6	β7	β8	β9
-0,1638	0,0410	0,2614
-0,5133	-0,4071	-0,1535
-1,0102	-0,8053	-0,5849	-0,2959	-0,1863
0,4625	0,5686	0,8222	0,5235	0,3628
-0,1863	-0,2959
0,3628	0,5235
qi

(продолжение табл. 14.13)

β10	β11	s1	s2	s3	s4	s5	s6	s7	s8
-0,4601	-0,7548	-0,5064
0,8879	0,6560	-0,8623
-0,4601	-0,7548	0,7188	0,8261	0,8895
0,8879	0,6560	0,6952	0,5635	0,4569
0,1076	0,3441	0,8261	0,8895	-0,5250	-0,5412
0,2638	0,1178	0,5635	0,4569	-0,8511	-0,8409
0,810	0,810	0,810	0,810	0,810	0,810	0,810	0,810

Шаг 4. Составление нормальных уравнений коррелат.

Источник