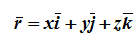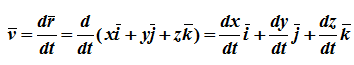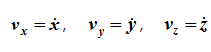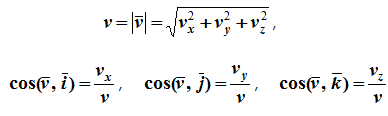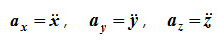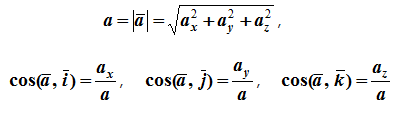iSopromat.ru
Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.
Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.
В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.
Векторный
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
Координатный
При координатном способе задания движения задаются координаты точки как функции времени:
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
Естественный
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Координатный способ задания движения точки.



В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы осей (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде:
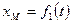
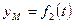
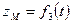
При координатном способе задания движения точки, траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами 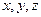
Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную 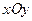
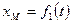
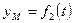
Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории.
При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).
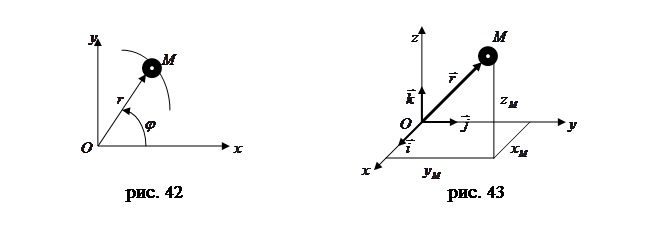 |
Положение точки в этом случае будут определять полярный угол 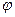
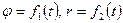
Векторный способ задания движения точки.
В этом случае положение точки в пространстве определяется только радиусом – вектором, проведенным из начала декартовой системы координат (рис. 43). Уравнение движения в этом случае имеет вид:
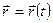
Векторный способ задания движения удобен для установления общих зависимостей, так как позволяет описать движение точки одним векторным уравнением вместо трех скалярных.
Источник
iSopromat.ru
Рассмотрим определение скорости и ускорения точек при координатном способе задания движения, а также, модуль и направление скоростей и ускорений и их проекции на оси координат:
Проекции скорости на оси координат равны производным соответствующих координат по времени:
Модуль и направление скорости определяются выражениями
Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени
Модуль и направление ускорения определяются выражениями
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Координатный способ задания движения точки
Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i , j , k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди
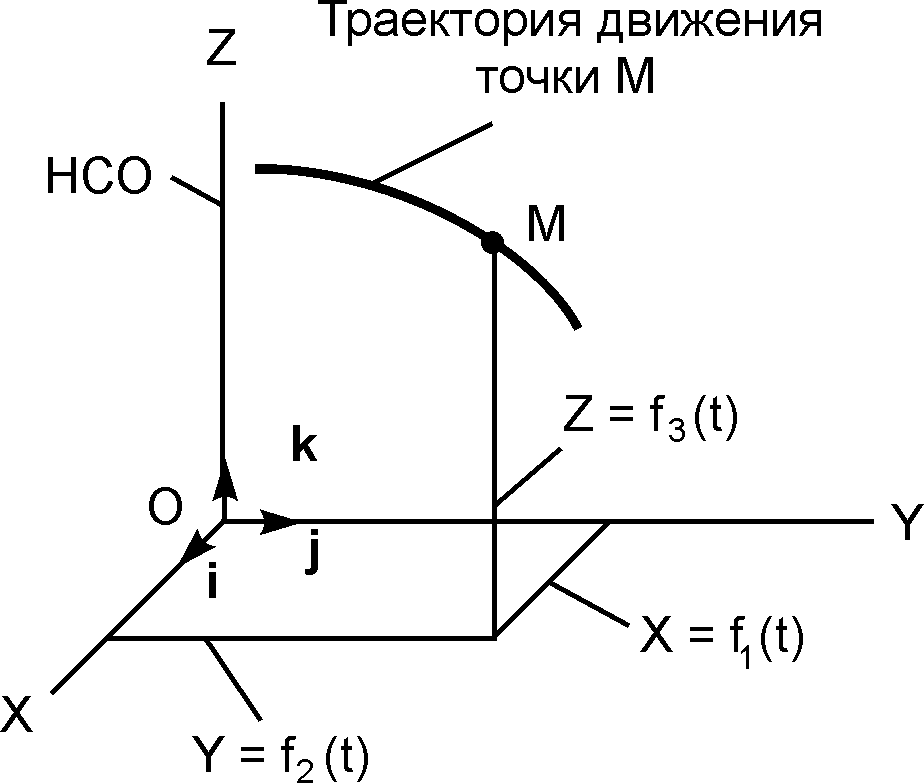 Рис. 2.1 Рис. 2.1 |
наты X, Y, Z движущейся точки М являются функциями времени t.
Систему трёх уравнений X = f1(t); Y = f2(t); Z = f3(t) называют уравнениями движения точки в пространстве в декартовых координатах.
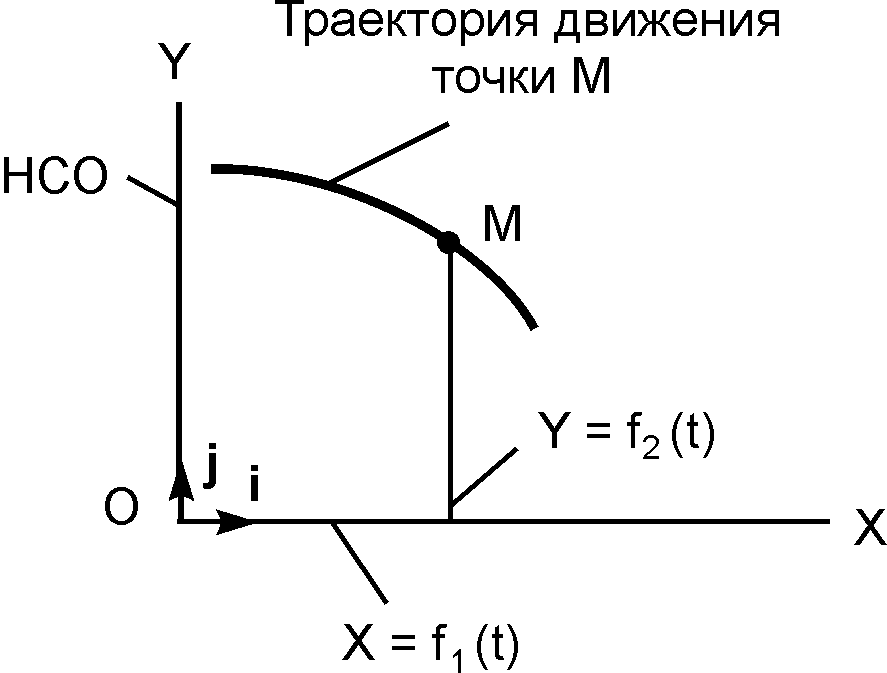 Рис. 2.2 Рис. 2.2 |
Пример: X = 10·t 2 + 1; Y = 7·t 3 + t 2 + 1; Z = 10·sin(·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.
Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f1(t); Y = f2(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.
Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t 2 + t 2 + t; Y = 7·cos(·t).
Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).
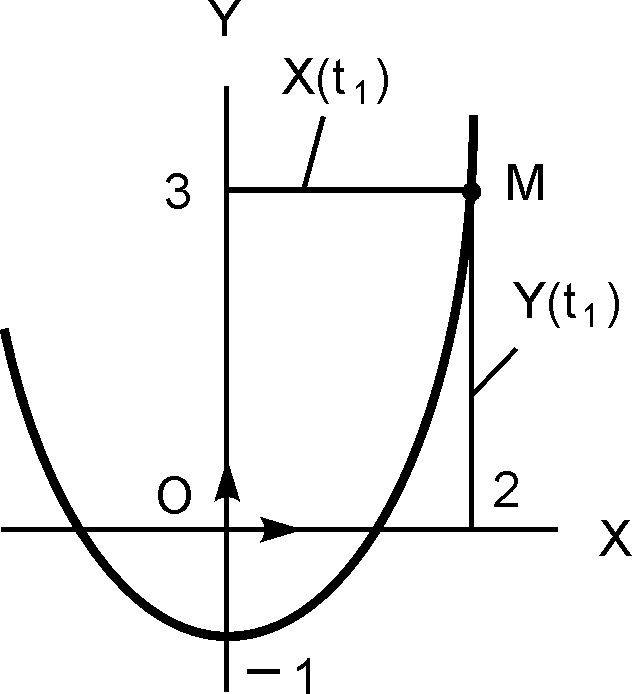 Рис. 2.3 Рис. 2.3 |
Пример. Заданы уравнения: X = 4·t (см); Y = 16·t 2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t1 = 0,5 с.
Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t 2 – 1. Получаем
Y = 16·(X/4) 2 – 1 = X 2 – 1.
Выражение Y = X 2 – 1 есть уравнение параболы (y = a · x 2 + b · x + c) с вершиной в точке с координатами (0, – 1). В момент времени t1 = 0,5 с определяем координаты:
Y(t1) = 16·(t1) 2 – 1 = 16·(0,5) 2 – 1 = 3 см >0.
Показываем положение точки на траектории её движения (рис. 2.3).
Пример. Дано: X = 3·sin(·t), см (1); Y = 3·cos(·t), см (2); t1 = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t1.
Решение. Уравнения движения точки представим в следующем виде: (X) 2 = (3·sin(·t)) 2 (1 I ); (Y) 2 = (3·cos(·t)) 2 (2 I ). Для решения используем тригонометрическую формулу sin 2 (α) + cos 2 (α) = 1.
Складывая левые и правые части уравнений (1 I ) и (2 I ), получим (X) 2 + (Y) 2 = 3 2 ·(sin 2 (·t) + cos 2 (·t)) = 3 2 ·1 или (X) 2 + (Y) 2 = 3 2 . Известно, что уравнение (X) 2 + (Y) 2 = R 2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка
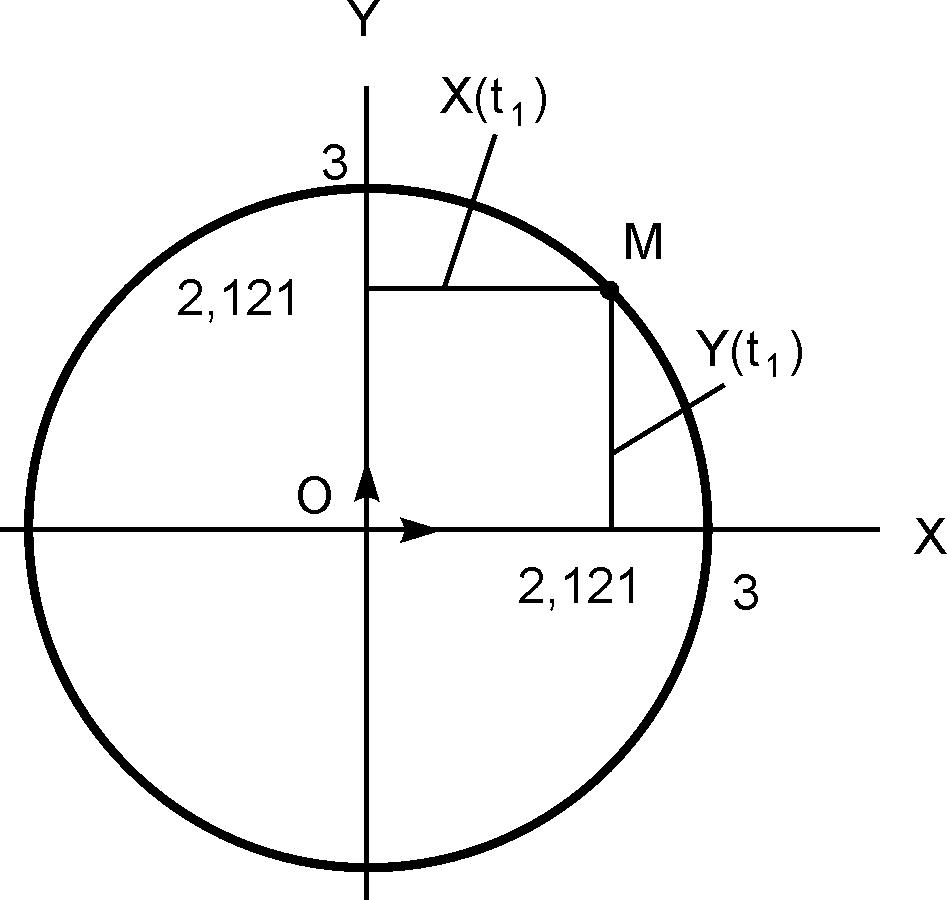 Рис. 2.4 Рис. 2.4 |
движется по окружности радиусом R = 3 см (рис. 2.4).
Определяем положение точки на траектории движения в момент времени t1.
Показываем точку на траектории её движения (см. рис. 2.4).
ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:
1) неверно определен вид траектории движения;
2) неверно рассчитаны значения координат X(t1), Y(t1).
Прямолинейное движение точки М определяется одним уравнением движения X = f(t).
Пример. Дано: X = 10·t 2 + sin(2··t) + 3, см (рис. 2.5).
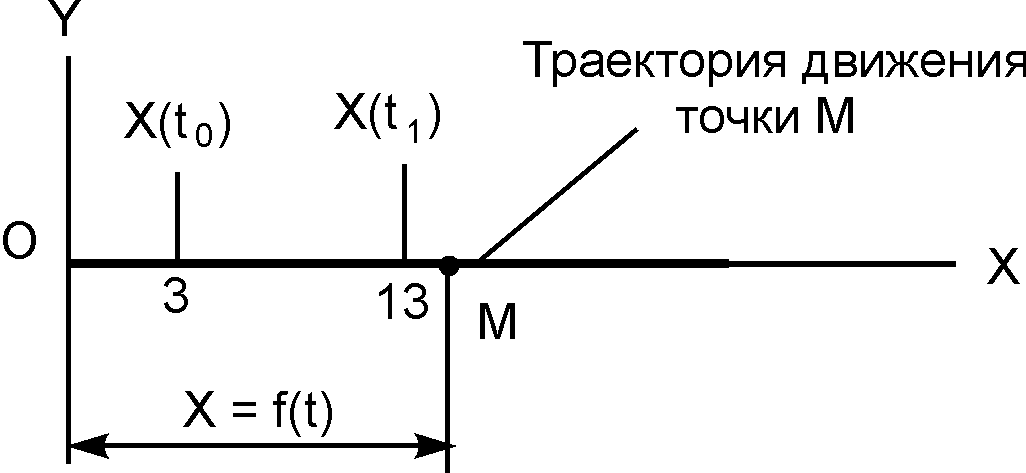 Рис. 2.5 Рис. 2.5 |
Определить положение точки на траектории движения в начальный момент времени t0 = 0 и в момент времени t1 = 1 c.
Решение.
X(t0) = 10·(t0) 2 + sin(2··t0) + 3 = 10·0 2 + sin(2··0) + 3 = 3 см > 0.
X(t1) = 10·(t1) 2 + sin(2··t1) + 3 = 10·1 2 + sin(2··1) + 3 = 13 см> 0.
Значения координат X(t0), X(t1) наносим на рис. 2.5.
Скорость точки
Скорость – векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчёта.
Скорость точки всегда направлена по касательной к траектории её движения.
 Рис. 2.6 Рис. 2.6 |
Пусть заданы уравнения движения точки в пространстве: X = f1(t); Y = f2(t); Z = f3(t) (рис. 2.6).
Разложим вектор V скорости точки на составляющие по координатным осям: V = VOX + VOY + VOZ. Векторы VOX, VOY, VOZ называют компонентами скорости по координатным осям. Вектор Vскорости можно выразить векторным равенством:
V = i· 

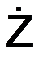
где 


В инженерных расчётах рекомендуется использовать следующие обозначения проекций скорости V на координатные оси: 

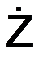
Сравнивая последние формулы, запишем равенство
V = VOX + VOY + VOZ = i· 

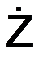
Из этого равенства имеем:
VOX = i· 

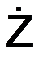
Проекции скорости на координатные оси системы отсчёта равны первым производным по времени от соответствующих уравнений движения:


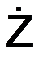
где точка (·) означает символ однократного дифференцирования функции по времени.
Зная проекции скорости на координатные оси, находят модуль скорости по формуле
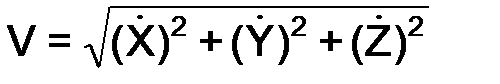
Ориентацию вектора скорости V в системе отсчёта OXYZ определяют по направляющим косинусам:
cos(V, i) = 

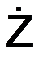
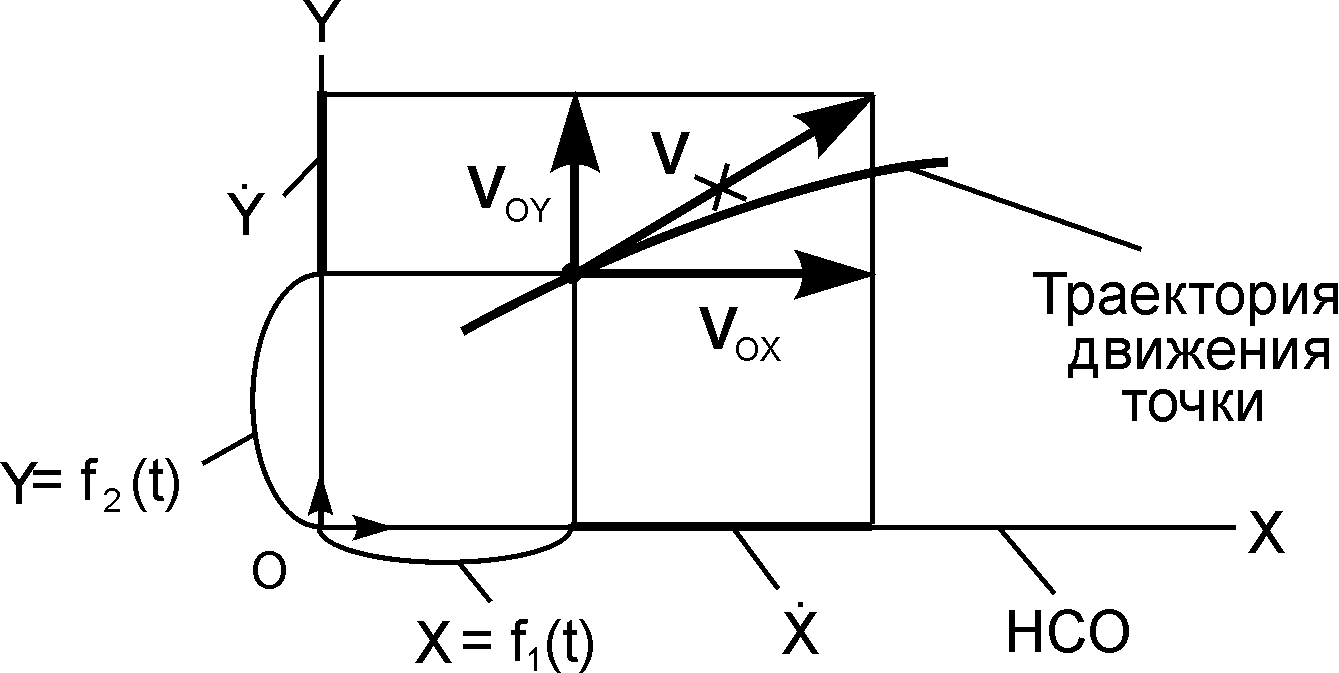 Рис. 2.7 Рис. 2.7 |
Движение точки в плоскости OXY (рис. 2.7) задаётся двумя уравнениями движения: X = f1(t); Y = f2(t).
Модуль и направление скорости точки в этом случае определяются по формулам:
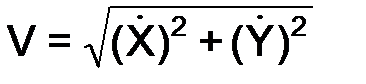



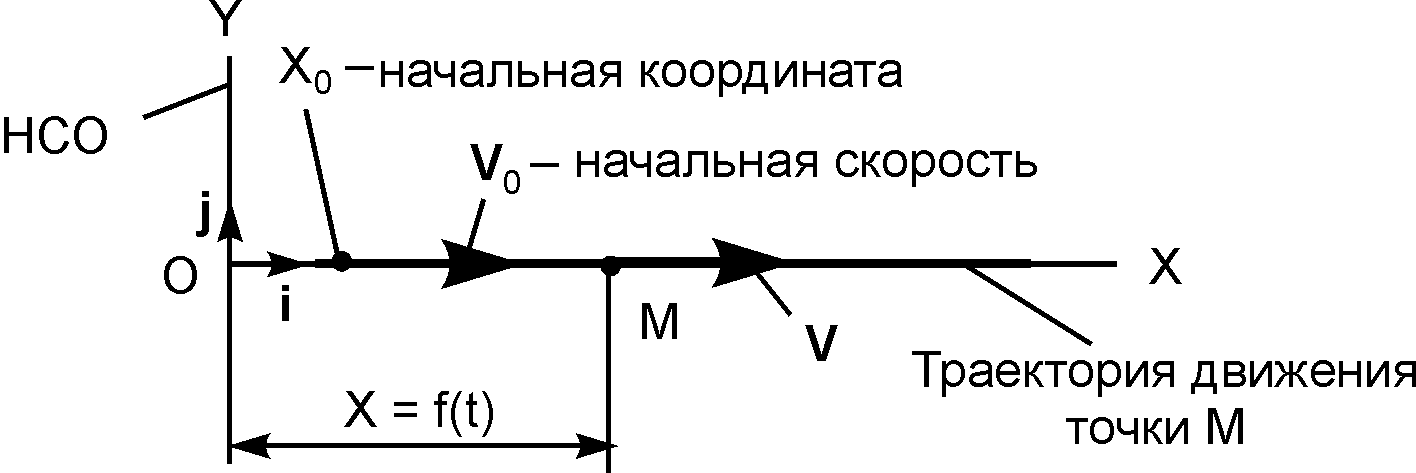 Рис. 2.8 Рис. 2.8 |
Прямолинейное движение точки (рис. 2.8) задаётся одним уравнением X = f(t).
В этом случае модуль скорости точки равен абсолютной величине проекции скорости на координатную ось ОХ.
V = | 
При 

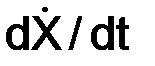

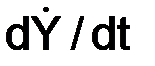
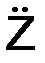
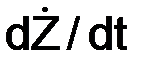
Модуль ускорения находится по следующим формулам:
a= 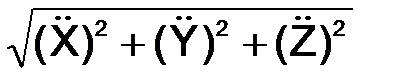
a = 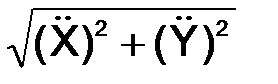
a =| 
Направляющие косинусы находятся по следующим формулам:
cos(a, i) = 

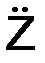
Зная направляющие косинусы, вектор ускорения а ориентируют в пространстве.
Рассматривается движение точки по прямой линии согласно заданному уравнению движения X = f(t) (рис. 2.10).
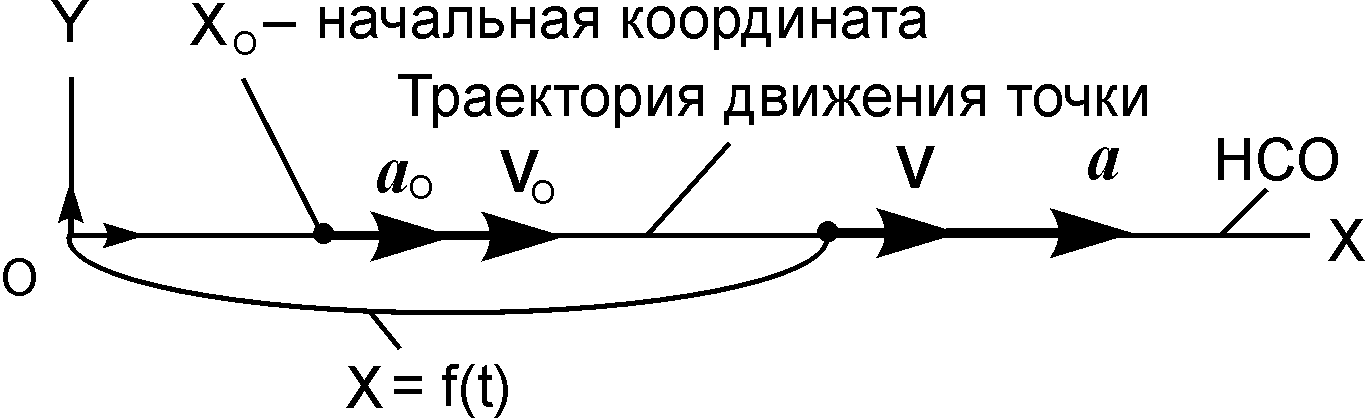 Рис. 2.10 Рис. 2.10 |
При таком движении справедливо равенство а = аОХ =i· 
Примечания:
1. Если проекции ускорения на координатные оси положительны ( 

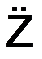
2. Если проекции ускорения на координатные оси отрицательны ( 



Если проекция 


X = X0 + 

где X0 – значение координаты точки в начальный момент времени; 
Если 
Если 









X = (t) 3 /3 + 
Таким образом, если заданы уравнения движения точки в координатной форме, то можно в любой момент времени определить следующие кинематические характеристики:
1) траекторию движения;
2) положение точки на траектории движения;
3) проекции скорости на координатные оси, а, следовательно, и модуль скорости;
4) ориентацию вектора скорости в системе отсчёта по её направляющим косинусам;
5) проекции ускорения на координатные оси и модуль ускорения;
6) положение вектора ускорения в системе отсчёта по его направляющим косинусам.
Естественный способ задания
Движения точки
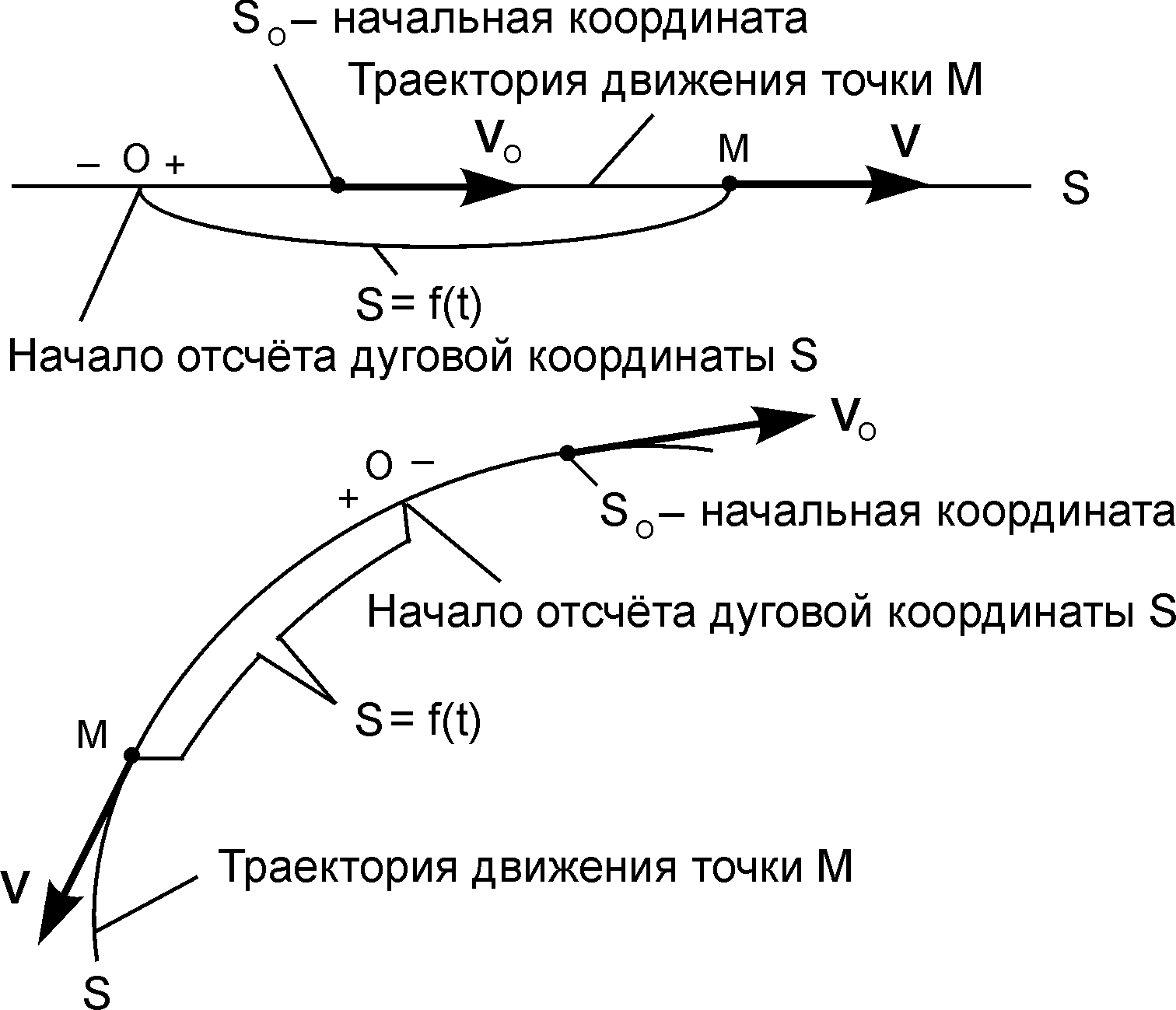 Рис. 2.11 Рис. 2.11 |
Естественный способ задания движения точки применяется в случае, когда траектория движения точки заранее известна. Траекторией могут быть как прямая, так и кривая линии (рис. 2.11).
На известной траектории движения точки выбирается неподвижная точка О, которую называют началом отсчёта дуговой координаты. Положение движущейся точки М на траектории определяется дуговой координатой, т. е. расстоянием ОМ = S, отложенным по траектории от начала отсчета О.
Прямую линию на рис. 2.11 можно считать дугой окружности, радиус которой равен бесконечности.
Расстояния, отложенные в одну сторону от точки О, условно считают положительным, а в противоположную сторону – отрицательным, т. е. устанавливается направление отсчета дуговой координаты. При движении точки М расстояние S от этой точки до неподвижной точки О изменяется с течением времени, т. е. дуговая координата S является функцией времени.
Эту зависимость называют уравнением движения точки в естественных координатах.
Если вид функции S = f(t) известен, то для каждого значения времени ti можно найти значение дуговой координаты Si, отложить соответствующее расстояние по траектории от начала отсчета О и указать, где находится движущаяся точка М в этот момент времени.
Таким образом, движение точки определено, если известны следующие элементы: вид траектории движения точки (прямая линия, окружность, эллипс и т. д.); начало отсчёта (точка О) дуговой координаты; положительное и отрицательное (+, –) направления отсчёта дуговой координаты; уравнение движения S = f ( t ).
Дуговую координату точки не следует смешивать с длиной пути, пройденного точкой за время t.
Пример. Пусть уравнение движения точки имеет вид S = 10·sin(·t) см. При начальном времени t0 = 0 начальная координата S0 = 0. При t1 = 0,5 cS(t1) = 10 см; при t2 = 1 cS(t2) = 0; при t3 = 1,5 cS(t3) = – 10 см; при t4 = 2 cS(t4) = 0.
Таким образом, за время t4 = 2 c точка М прошла путь, равный 40 см, а её дуговая координата S4 в этот момент времени равна нулю.
Дата добавления: 2020-04-25 ; просмотров: 146 ; Мы поможем в написании вашей работы!
Источник