Умножение векторов матричным способом

Содержание

Произведение матриц и векторов, элементы линейной алгебры
Матричное умножение
Векторное умножение
Умножение вектора на матрицу
Элементы линейной алгебры
Видео по теме
Умножение матриц
Согласованные матрицы
Определение умножения
Умножение квадратных матриц
Основные свойства матричного произведения
Случай прямоугольных матриц
Вектор-строки и вектор-столбцы
Возведение матрицы в степень

Произведение матриц и векторов, элементы линейной алгебры

Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую:

В консоли увидим результат:

array([[ 10, 22, 36],
[ 52, 70, 90],
[112, 136, 162]])

Матричное умножение

Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:

то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду:

Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:

array([[ 84, 90, 96],
[201, 216, 231],
[318, 342, 366]])

Тот же результат можно получить и с помощью функции:

Считается, что этот вариант предпочтительнее использовать при умножении матриц.

Векторное умножение

Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:

то их умножение можно реализовать в двух видах:

Первое умножение реализуется либо через функцию:

Либо, более предпочтительной функцией для внутреннего умножения векторов:

Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:

получим результат в виде следующей матрицы:

array([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[7., 7., 7., 7., 7., 7., 7., 7., 7.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])

Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:

или, с использованием матриц:

Умножение вектора на матрицу

Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:

Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:

И, затем, воспользуемся уже знакомой нам функцией dot:

При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.

Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:

Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:

Определим массивa в два элемента и умножим на матрицу b:

Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде:

Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:

Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):

Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.

Элементы линейной алгебры

Из высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций.

Предположим, имеется квадратная матрица 3×3:

Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:

Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:

Здесь — некие числа линейного уравнения. Например, возьмем их равными:

Тогда корни уравнения можно вычислить с помощью функции solve:

Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:

Откуда получаем решения :

На уровне пакета NumPy это делается так:

Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.

Описание

linalg.cholesky()

Разложение Холецкого

linalg.qr()

QR-разложение матрицы

linalg.svd()

Сингулярное (SVD) разложение матрицы

linalg.norm()

Норма матрицы или вектора

linalg.cond()

Число обусловленности матрицы

linalg.det()

Определитель (детерминант) матрицы

linalg.matrix_rank()

Вычисление ранга матрицы по алгоритму SVD

Сумма диагональных элементов массива

linalg.eig()

Вычисление собственных значений и правых собственных векторов

linalg.eigvals()

Вычисление собственных значений матрицы

linalg.solve()

Решение линейного матричного уравнения

linalg.tensorsolve()

Решение линейного тензорного уравнения

linalg.lstsq()

Решает задачу поиска наименьших квадратов для линейного матричного уравнения

linalg.inv()

Вычисление обратной матрицы

linalg.pinv()

Вычисление псевдообратной (Мура-Пенроуза) матрицы

linalg.tensorinv()

Вычисление обратного тензора (N-мерного массива)

Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Источник

Умножение матриц

Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.

Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.

Согласованные матрицы

Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=\left[ m\times n \right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.

Определение. Матрицы вида $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются .

Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:

Нам важен порядок матриц. Например, матрицы $A=\left[ 3\times 2 \right]$ и $B=\left[ 2\times 5 \right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=\left[ 2\times 5 \right]$ и $A=\left[ 3\times 2 \right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.

Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $\left[ n\times n \right]$ согласованы всегда.

В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $\left( 1;0 \right)$ и $\left( 0;1 \right)$ задают разные точки на плоскости.

Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $\left( A;B \right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».

Ну и что с того?

Определение умножения

Рассмотрим две согласованные матрицы: $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$. И определим для них операцию умножения.

Определение. $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ — это новая матрица $C=\left[ m\times k \right]$, элементы которой считаются по формуле:

Обозначается такое произведение стандартно: $C=A\cdot B$.

По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]

У тех, кто впервые видит это определение, сразу возникает два вопроса:

Что это за лютая дичь?
А почему так сложно?

Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?

Прежде всего заметим, что длинная строчка для расчёта $<_>$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:

Берём $i$-ю строку в первой матрице;
Берём $j$-й столбец во второй матрице;
Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.

Данный процесс легко понять по картинке:

Схема перемножения двух матриц

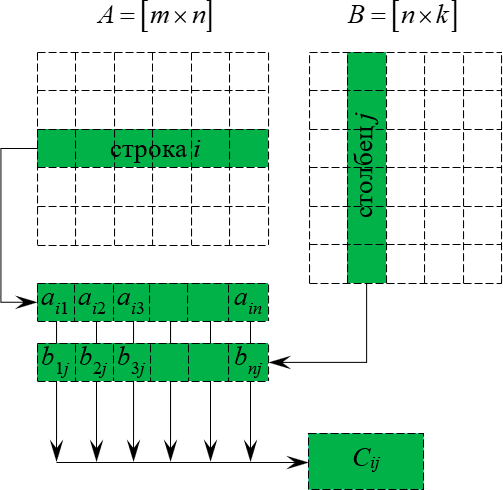
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем $<_>$. И так для всех $1\le i\le m$ и $1\le j\le k$. Т.е. всего будет $m\times k$ таких «извращений».

На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:

Тогда их скалярным произведением будет именно сумма попарных произведений:

По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $\overrightarrow$ на вектор-столбец $\overrightarrow$.

Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.

Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.

Умножение квадратных матриц

\[\left[ \begin<*<35>> 1 & 2 \\ -3 & 4 \\\end \right]\cdot \left[ \begin<*<35>> -2 & 4 \\ 3 & 1 \\\end \right]\]

Решение. Итак, у нас две матрицы: $A=\left[ 2\times 2 \right]$ и $B=\left[ 2\times 2 \right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:

\[\begin & \left[ \begin<*<35>> 1 & 2 \\ -3 & 4 \\\end \right]\cdot \left[ \begin<*<35>> -2 & 4 \\ 3 & 1 \\\end \right]=\left[ \begin<*<35>> 1\cdot \left( -2 \right)+2\cdot 3 & 1\cdot 4+2\cdot 1 \\ -3\cdot \left( -2 \right)+4\cdot 3 & -3\cdot 4+4\cdot 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 4 & 6 \\ 18 & -8 \\\end \right]. \end\]

Задача 2. Выполните умножение:

\[\left[ \begin 1 & 3 \\ 2 & 6 \\\end \right]\cdot \left[ \begin<*<35>>9 & 6 \\ -3 & -2 \\\end \right]\]

Решение. Опять согласованные матрицы, поэтому выполняем действия:\[\]

\[\begin & \left[ \begin 1 & 3 \\ 2 & 6 \\\end \right]\cdot \left[ \begin<*<35>> 9 & 6 \\ -3 & -2 \\\end \right]=\left[ \begin<*<35>> 1\cdot 9+3\cdot \left( -3 \right) & 1\cdot 6+3\cdot \left( -2 \right) \\ 2\cdot 9+6\cdot \left( -3 \right) & 2\cdot 6+6\cdot \left( -2 \right) \\\end \right]= \\ & =\left[ \begin 0 & 0 \\ 0 & 0 \\\end \right]. \end\]

Как видим, получилась матрица, заполненная нулями

Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.

В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.

Основные свойства матричного произведения

В двух словах. Умножение матриц:

Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;

Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.

Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

\[\left[ \begin<*<35>> 1 & 2 \\ -3 & 4 \\\end \right]\cdot \left[ \begin<*<35>> -2 & 4 \\ 3 & 1 \\\end \right]=\left[ \begin<*<35>>4 & 6 \\ 18 & -8 \\\end \right]\]

Но если поменять матрицы местами, то получим совсем другой результат:

\[\left[ \begin<*<35>> -2 & 4 \\ 3 & 1 \\\end \right]\cdot \left[ \begin<*<35>> 1 & 2 \\ -3 & 4 \\\end \right]=\left[ \begin -14 & 4 \\ 0 & 10 \\\end \right]\]

Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left[ 2\times 3 \right]$ и $\left[ 3\times 5 \right]$ вполне себе согласованы в указанном порядке, но те же матрицы $\left[ 3\times 5 \right]$ и $\left[ 2\times 3 \right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(

Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)

Тем не менее, умножение матриц ассоциативно:

\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left[ n\times n \right]$. Множество всех таких матриц обозначается $<^>$ (т.е. записи $A=\left[ n\times n \right]$ и \[A\in <^>\] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.

Определение. размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=\left[ n\times n \right]$ выполняется равенство:

\[A\cdot E=E\cdot A=A\]

Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

Случай прямоугольных матриц

А ничего — всё то же самое, что и с квадратными.

\[\left[ \begin \begin 5 \\ 2 \\ 3 \\\end & \begin 4 \\ 5 \\ 1 \\\end \\\end \right]\cdot \left[ \begin<*<35>> -2 & 5 \\ 3 & 4 \\\end \right]\]

Решение. Имеем две матрицы: $A=\left[ 3\times 2 \right]$ и $B=\left[ 2\times 2 \right]$. Выпишем числа, обозначающие размеры, в ряд:

Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=\left[ 3\times 2 \right]$:

\[\begin & \left[ \begin \begin 5 \\ 2 \\ 3 \\\end & \begin 4 \\ 5 \\ 1 \\\end \\\end \right]\cdot \left[ \begin<*<35>> -2 & 5 \\ 3 & 4 \\\end \right]=\left[ \begin<*<35>> 5\cdot \left( -2 \right)+4\cdot 3 & 5\cdot 5+4\cdot 4 \\ 2\cdot \left( -2 \right)+5\cdot 3 & 2\cdot 5+5\cdot 4 \\ 3\cdot \left( -2 \right)+1\cdot 3 & 3\cdot 5+1\cdot 4 \\\end \right]= \\ & =\left[ \begin<*<35>> 2 & 41 \\ 11 & 30 \\ -3 & 19 \\\end \right]. \end\]

Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=\left[ 3\times 2 \right]$.

Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?

Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.

Задача 4. Найдите все возможные попарные произведения матриц:

Решение. Для начала запишем размеры матриц:

\[A=\left[ 2\times 4 \right];\ B=\left[ 4\times 2 \right];\ C=\left[ 2\times 2 \right]\]

Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:

\[A\cdot B=\left[ \begin<*<35>> 1 & -1 & 2 & -2 \\ 1 & 1 & 2 & 2 \\\end \right]\cdot \left[ \begin<*<35>> 0 & 1 \\ 2 & 0 \\ 0 & 3 \\ 4 & 0 \\\end \right]=\left[ \begin<*<35>>-10 & 7 \\ 10 & 7 \\\end \right]\]

Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:

\[A \cdot B=\left[ 2\times 4 \right]\cdot \left[ 4\times 2 \right]=\left[ 2\times 2 \right]\]

Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.

Какие ещё возможны варианты? Безусловно, можно найти $B\cdot A$, поскольку $B=\left[ 4\times 2 \right]$, $A=\left[ 2\times 4 \right]$, поэтому упорядоченная пара $\left( B;A \right)$ является согласованной, а размерность произведения будет:

\[B \cdot A=\left[ 4\times 2 \right]\cdot \left[ 2\times 4 \right]=\left[ 4\times 4 \right]\]

Короче говоря, на выходе будет матрица $\left[ 4\times 4 \right]$, коэффициенты которой легко считаются:

\[B\cdot A=\left[ \begin<*<35>> 0 & 1 \\ 2 & 0 \\ 0 & 3 \\ 4 & 0 \\\end \right]\cdot \left[ \begin<*<35>> 1 & -1 & 2 & -2 \\ 1 & 1 & 2 & 2 \\\end \right]=\left[ \begin<*<35>>1 & 1 & 2 & 2 \\ 2 & -2 & 4 & -4 \\ 3 & 3 & 6 & 6 \\ 4 & -4 & 8 & -8 \\\end \right]\]

Очевидно, можно согласовать ещё $C\cdot A$ и $B\cdot C$ — и всё. Поэтому просто запишем полученные произведения:

\[C\cdot A=\left[ \begin<*<35>> 1 & 1 & 2 & 2 \\ 1 & -1 & 2 & -2 \\\end \right]\]

\[B\cdot C=\left[ \begin<*<35>>1 & 0 \\ 0 & 2 \\ 3 & 0 \\ 0 & 4 \\\end \right]\]

Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.

Но на этом история не заканчивается. Переходим к частным случаям умножения.:)

Вектор-строки и вектор-столбцы

Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.

Определение. — это матрица размера $\left[ m\times 1 \right]$, т.е. состоящая из нескольких строк и только одного столбца.

— это матрица размера $\left[ 1\times n \right]$, т.е. состоящая из одной строки и нескольких столбцов.

\[\left[ \begin<*<35>> 2 & -1 & 3 \\ 4 & 2 & 0 \\ -1 & 1 & 1 \\\end \right]\cdot \left[ \begin<*<35>> 1 \\ 2 \\ -1 \\\end \right]\]

Решение. Перед нами произведение согласованных матриц: $\left[ 3\times 3 \right]\cdot \left[ 3\times 1 \right]=\left[ 3\times 1 \right]$. Найдём это произведение:

\[\left[ \begin<*<35>> 2 & -1 & 3 \\ 4 & 2 & 0 \\ -1 & 1 & 1 \\\end \right]\cdot \left[ \begin<*<35>> 1 \\ 2 \\ -1 \\\end \right]=\left[ \begin<*<35>> 2\cdot 1+\left( -1 \right)\cdot 2+3\cdot \left( -1 \right) \\ 4\cdot 1+2\cdot 2+0\cdot 2 \\ -1\cdot 1+1\cdot 2+1\cdot \left( -1 \right) \\\end \right]=\left[ \begin<*<35>> -3 \\ 8 \\ 0 \\\end \right]\]

Задача 6. Выполните умножение:

\[\left[ \begin<*<35>> 1 & 2 & -3 \\\end \right]\cdot \left[ \begin<*<35>> 3 & 1 & -1 \\ 4 & -1 & 3 \\ 2 & 6 & 0 \\\end \right]\]

Решение. Опять всё согласовано: $\left[ 1\times 3 \right]\cdot \left[ 3\times 3 \right]=\left[ 1\times 3 \right]$. Считаем произведение:

\[\left[ \begin<*<35>> 1 & 2 & -3 \\\end \right]\cdot \left[ \begin<*<35>> 3 & 1 & -1 \\ 4 & -1 & 3 \\ 2 & 6 & 0 \\\end \right]=\left[ \begin<*<35>>5 & -19 & 5 \\\end \right]\]

На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)

Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).

Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.

Возведение матрицы в степень

Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.

Такие произведения всегда согласованы:

\[A\cdot A=\left[ n\times n \right]\cdot \left[ n\times n \right]=\left[ n\times n \right]\]

И обозначаются точно так же, как и обычные степени:

На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:

Задача 7. Возведите матрицу в указанную степень:

Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<2>>=\left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1\cdot 1+1\cdot 0 & 1\cdot 1+1\cdot 1 \\ 0\cdot 1+1\cdot 0 & 0\cdot 1+1\cdot 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 2 \\ 0 & 1 \\\end \right] \end\]

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>= <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 2 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 3 \\ 0 & 1 \\\end \right] \end\]

Ответ: $\left[ \begin1 & 3 \\ 0 & 1 \\\end \right]$.

Задача 8. Возведите матрицу в указанную степень:

Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<10>>= <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left( \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right] \right)\cdot \left( \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right] \right)= \\ & =\left[ \begin 1 & 6 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 4 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin 1 & 10 \\ 0 & 1 \\\end \right] \end\]

Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.

Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:

Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.

В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $\left[ 3\times 3 \right]$.

Задача 9. Возведите матрицу в указанную степень:

Решение. Не будем искать закономерности. Работаем «напролом»:

\[ <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<3>>= <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<2>>\cdot \left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]\]

Для начала возведём эту матрицу в квадрат:

\[\begin & <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<2>>=\left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]\cdot \left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]= \\ & =\left[ \begin<*<35>> 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\\end \right] \end\]

Теперь возведём в куб:

\[\begin & <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<3>>=\left[ \begin<*<35>> 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\\end \right]\cdot \left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]= \\ & =\left[ \begin<*<35>> 2 & 3 & 3 \\ 3 & 2 & 3 \\ 3 & 3 & 2 \\\end \right] \end\]

Вот и всё. Задача решена.

Ответ: $\left[ \begin 2 & 3 & 3 \\ 3 & 2 & 3 \\ 3 & 3 & 2 \\\end \right]$.

Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)

На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.

Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.

Источник
Читайте также: Числа с плавающей запятой способы представления