Умножение матриц
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Одна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=\left[ m\times n \right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Определение. Матрицы вида $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, в которых количество столбцов в первой матрице совпадает с количеством строк во второй, называются .
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
- Нам важен порядок матриц. Например, матрицы $A=\left[ 3\times 2 \right]$ и $B=\left[ 2\times 5 \right]$ являются согласованными (2 столбца в первой матрице и 2 строки во второй), а вот наоборот — матрицы $B=\left[ 2\times 5 \right]$ и $A=\left[ 3\times 2 \right]$ — уже не согласованы (5 столбцов в первой матрице — это как бы не 3 строки во второй).
- Согласованность легко проверить, если выписать все размеры друг за другом. На примере из предыдущего пункта: «3 2 2 5» — посередине одинаковые числа, поэтому матрицы согласованы. А вот «2 5 3 2» — не согласованы, поскольку посередине разные числа.
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $\left[ n\times n \right]$ согласованы всегда.
В математике, когда важен порядок перечисления объектов (например, в рассмотренном выше определении важен порядок матриц), часто говорят об упорядоченных парах. Мы встречались с ними ещё в школе: думаю, и ежу понятно, что координаты $\left( 1;0 \right)$ и $\left( 0;1 \right)$ задают разные точки на плоскости.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $\left( A;B \right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй».
Ну и что с того?
Определение умножения
Рассмотрим две согласованные матрицы: $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$. И определим для них операцию умножения.
Определение. $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ — это новая матрица $C=\left[ m\times k \right]$, элементы которой считаются по формуле:
Обозначается такое произведение стандартно: $C=A\cdot B$.
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
- Что это за лютая дичь?
- А почему так сложно?
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Прежде всего заметим, что длинная строчка для расчёта $<
- Берём $i$-ю строку в первой матрице;
- Берём $j$-й столбец во второй матрице;
- Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.
Данный процесс легко понять по картинке:
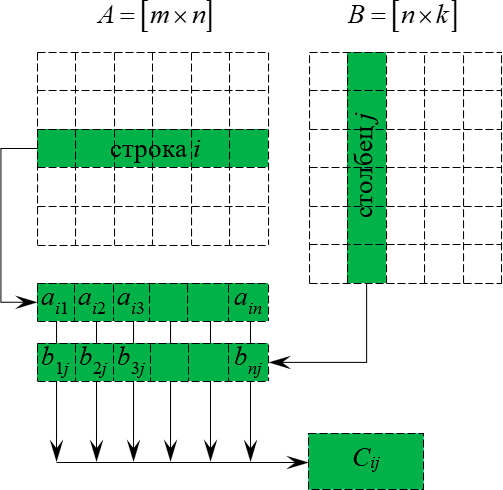
Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем $<
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
Тогда их скалярным произведением будет именно сумма попарных произведений:
По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $\overrightarrow$ на вектор-столбец $\overrightarrow$.
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
\[\left[ \begin
Решение. Итак, у нас две матрицы: $A=\left[ 2\times 2 \right]$ и $B=\left[ 2\times 2 \right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение:
\[\begin
Задача 2. Выполните умножение:
\[\left[ \begin
Решение. Опять согласованные матрицы, поэтому выполняем действия:\[\]
\[\begin
Как видим, получилась матрица, заполненная нулями
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
- Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
- Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
- Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
\[\left[ \begin
Но если поменять матрицы местами, то получим совсем другой результат:
\[\left[ \begin
Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left[ 2\times 3 \right]$ и $\left[ 3\times 5 \right]$ вполне себе согласованы в указанном порядке, но те же матрицы $\left[ 3\times 5 \right]$ и $\left[ 2\times 3 \right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Среди квадратных матриц заданного размера $n$ всегда найдутся такие, которые дают одинаковый результат как при перемножении в прямом, так и в обратном порядке. Как описать все подобные матрицы (и сколько их вообще) — тема для отдельного урока. Сегодня не будем об этом.:)
Тем не менее, умножение матриц ассоциативно:
\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left[ n\times n \right]$. Множество всех таких матриц обозначается $<
Определение. размера $n$ — это такая матрица $E$, что для любой квадратной матрицы $A=\left[ n\times n \right]$ выполняется равенство:
\[A\cdot E=E\cdot A=A\]
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
\[\left[ \begin
Решение. Имеем две матрицы: $A=\left[ 3\times 2 \right]$ и $B=\left[ 2\times 2 \right]$. Выпишем числа, обозначающие размеры, в ряд:
Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=\left[ 3\times 2 \right]$:
\[\begin
Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=\left[ 3\times 2 \right]$.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
Решение. Для начала запишем размеры матриц:
\[A=\left[ 2\times 4 \right];\ B=\left[ 4\times 2 \right];\ C=\left[ 2\times 2 \right]\]
Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение:
\[A\cdot B=\left[ \begin
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
\[A \cdot B=\left[ 2\times 4 \right]\cdot \left[ 4\times 2 \right]=\left[ 2\times 2 \right]\]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
Какие ещё возможны варианты? Безусловно, можно найти $B\cdot A$, поскольку $B=\left[ 4\times 2 \right]$, $A=\left[ 2\times 4 \right]$, поэтому упорядоченная пара $\left( B;A \right)$ является согласованной, а размерность произведения будет:
\[B \cdot A=\left[ 4\times 2 \right]\cdot \left[ 2\times 4 \right]=\left[ 4\times 4 \right]\]
Короче говоря, на выходе будет матрица $\left[ 4\times 4 \right]$, коэффициенты которой легко считаются:
\[B\cdot A=\left[ \begin
Очевидно, можно согласовать ещё $C\cdot A$ и $B\cdot C$ — и всё. Поэтому просто запишем полученные произведения:
\[C\cdot A=\left[ \begin
\[B\cdot C=\left[ \begin
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Определение. — это матрица размера $\left[ m\times 1 \right]$, т.е. состоящая из нескольких строк и только одного столбца.
— это матрица размера $\left[ 1\times n \right]$, т.е. состоящая из одной строки и нескольких столбцов.
\[\left[ \begin
Решение. Перед нами произведение согласованных матриц: $\left[ 3\times 3 \right]\cdot \left[ 3\times 1 \right]=\left[ 3\times 1 \right]$. Найдём это произведение:
\[\left[ \begin
Задача 6. Выполните умножение:
\[\left[ \begin
Решение. Опять всё согласовано: $\left[ 1\times 3 \right]\cdot \left[ 3\times 3 \right]=\left[ 1\times 3 \right]$. Считаем произведение:
\[\left[ \begin
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
\[A\cdot A=\left[ n\times n \right]\cdot \left[ n\times n \right]=\left[ n\times n \right]\]
И обозначаются точно так же, как и обычные степени:
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
\[\begin
\[\begin
Ответ: $\left[ \begin
Задача 8. Возведите матрицу в указанную степень:
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
\[\begin
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $\left[ 3\times 3 \right]$.
Задача 9. Возведите матрицу в указанную степень:
Решение. Не будем искать закономерности. Работаем «напролом»:
\[ <<\left[ \begin
Для начала возведём эту матрицу в квадрат:
\[\begin
Теперь возведём в куб:
\[\begin
Вот и всё. Задача решена.
Ответ: $\left[ \begin
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Источник




